基于 MATLAB的车削细长轴过程非线性振动分析

冯静,赵俊波,陶然

(1.郑州大学机械工程学院,郑州 450001;2.郑州交通职业学院,郑州 450062)

0 引言

在车削加工中,经常会产生振动,而振动产生的原因非常复杂,振动不仅恶化加工表面的质量,缩短了刀具和机床的寿命,尤其是共振时,使加工根本无法进行.通过建立车削系统的振动模型,研究车削过程中的振动及其稳定性,可以为工程中的应用提供一定的参考依据[1]。

车削过程是一个非常复杂的动态切削过程。在这个动态切削过程中,切削力和系统刚度都存在一定的变化规律。此处我们简化车削系统模型为单自由度,考虑了刚度的非线性变化,分析了该简化系统在切削过程的稳定性。基于上述内容,本文建立了车削系统单自由度非线性振动模型,并考虑其非线性刚度,应用 Matlab数值仿真程序分析了该系统的非线性振动稳定性问题。

1 建立该系统的力学模型

图 1所示分别为一个单自由度车削系统及其简化力学模型。其中 m为无弹性的等效质量,k为无质量等效弹簧刚度,c为等效阻尼。x(t)为系统振动位移,F(t)为切削过程中的激振力。为分析简便起见,通常将激振力看成服从简谐规律的交变力。

图 1 单自由度车削系统的加工模型和力学模型

不考虑作用在物体上的重力 mg时,该系统的振动方程可以表达为：

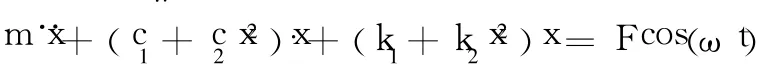
式中,mx为惯性力,方向与位移方向一致;(k1+k2x2)x为弹簧的恢复力,方向与位移方向相反;(c1+c2x2)x﹒为粘性阻尼力,其数值与物体的速度成正比,方向与位移方向相反;F即为背向力Fy,处于极面内并与工件轴线垂直,正是由于背向力的存在,才使工件在切削过程中产生了振动,直接影响工件的加工精度和表面粗糙度。实际工程计算中,背向力的计算仍以采用经验公式为主[2]：

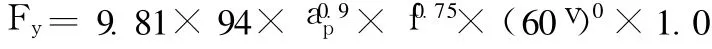
式中,ap—背吃刀量,单位 mm;f—进给量,单位 mm;v—切削速度,单位 m/s。

实验条件为：工件材料为 45钢,工件质量 m=3.77kg,当 ap=0.3mm,f=0.78mm,v=76m/min时,计算出 Fy=301.6N。

2 数值仿真及计算结果分析

设 x=x1,x﹒=x2,则非线性振动系统的方程可改写为状态方程的形式：

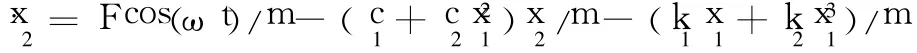
其中该系统的固有频率为wn=1310rad/s,为了更好地对激振频率 ω接近于固有角频率 ωn,以及在固有频率附近变动时系统的动力学行为,在 Matlab中采用龙格库塔法对上式编程进行求解绘图,可得到系统的分岔图和频率谱图如图 2所示。

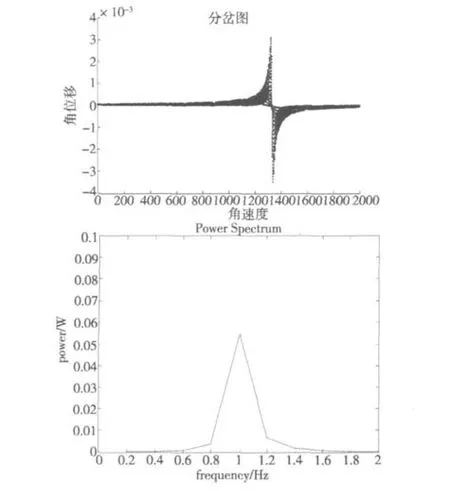
图 2 系统的分岔图和频率谱图

由以上分叉图可以看出角速度ω在1300左右出现分岔,说明在此处附近存在混沌或非线性振动,依图选取ω等于 1550rad/s,1320rad/s,950rad/s,500rad/s,280rad/s可计算得出相应相图和庞加莱截面如图3～7。

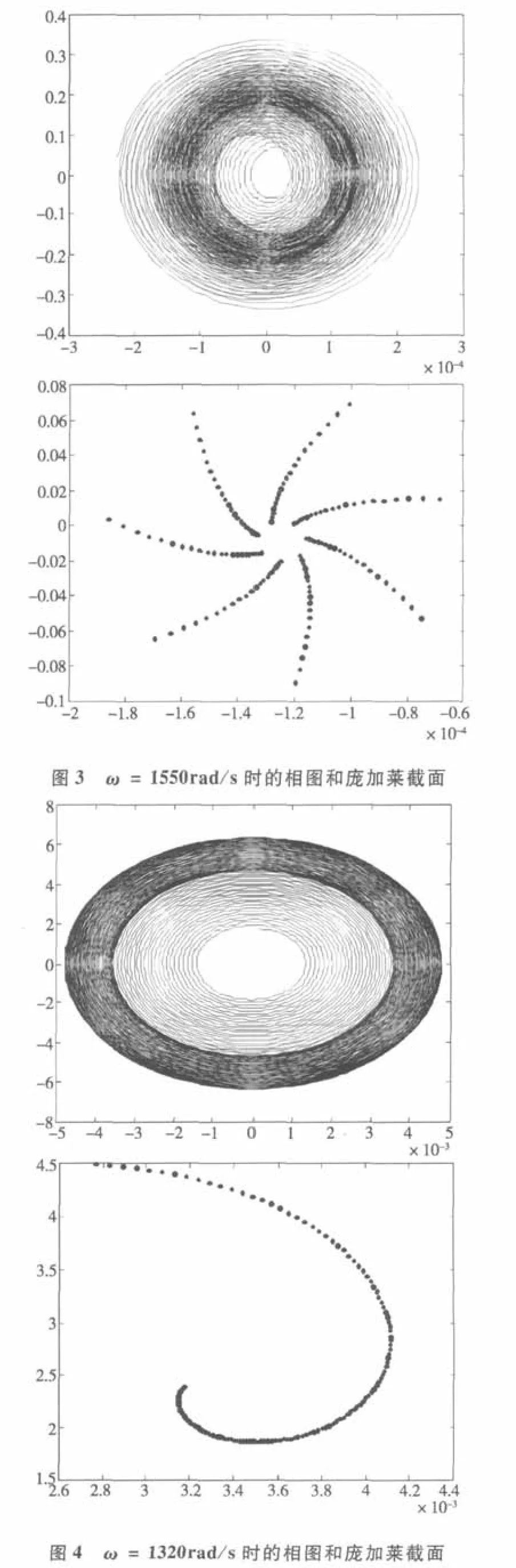
由图 3知,当 ω=1550rad/s时,系统处于倍周期运动,但相图中反映的运动是趋于一个极限环的,即鲁棒稳定,其 Poincare截面图收敛于一环面,也反映了鲁棒稳定性。图 4中转速进一步减小到ω=1320rad/s,因为此时的激振频率接近系统的固有频率,所以系统出现局部混沌,其运动态是有一定厚度的环状区域,这说明系统的运动虽不稳定,但按混沌规律运行,此时的Poincare截面图也由一条曲线趋近于一点。图 5中当转速减小至 ω=950rad/s时,系统相图中出现不稳定极限环,系统由倍周期运动向准周期运动过渡。图 6中的相图所反映的系统混沌态出现了奇怪吸引子而且每个吸引子的振动幅度都比较大,其 Poincare截面图也变为三条曲线,最终收敛于一点。在图 7中 ω=280rad/s,其相图表现为无数个吸引子在运动,但最终每个吸引子都围绕着一个极限环运动,仍属于鲁棒稳定,其Poincare截面图收敛于不规则的点也说明了其相对稳定性。

3 结束语

(1)建立了车削系统单自由度非线性振动模型,并应用 Matlab数值仿真程序得到系统的分岔图、频率谱图、相图和相应的 Poincare截面图,从而获知系统的振动特性。

(2)系统的转速是影响系统运动状态的重要因素。当转速较高时,系统处于相对稳定状态,但当转速降低时,会出现奇怪吸引子,使系统偏离原有的运动状态。这在车削加工启动和制动时应该考虑将车刀迅速脱离工件表面,以免影响工件质量。

(3)通过对车削系统非线性振动模型的仿真,可知其仿真结果与现场运行情况是相符合的。

[1]刘志超.非刚性轴无振动车削实验研究[J].矿山机械,2006,34(9)：117-118.

[2]张琳娜.动态车削过程及其非线性特征[J].郑州工学院学报,1993,14(4)：6-8.

[3]罗玉军,高尚晗,高中庸,等.动态切削力对切削颤振的影响[J].机械设计与制造,2007(11)：83-84.

[4]张智海,郑力,李志忠,等.端铣工艺非线性动力学特性的研究[J].机械工程学报,2004,40(8)：8-10.

[5]丁旺才,张有强,张庆爽.含干摩擦振动系统的非线性动力学分析[J].工程力学,2008,25(10)：212-217.

[6]张伟刚,高尚晗,龙新华,等.机床主轴滚动轴承系统非线性动力学分析[J].振动与冲击2008,27(9)：72-75.

[7]孟令启,马金亮,黄其柏.基于 Matlab的 4200轧机垂直振动仿真[J].钢铁研究学报2007,19(7)：58-62.

[8]孟令启,徐如松,王建勋,等.中厚板轧机非线性参激的振动[J].重庆大学学报,2008,31(4)：393-396.

[9]刘延柱,陈立群.非线性振动[M].北京：高等教育出版社,2001.