随机圆覆盖面积的统计分布

汪文俊，陈 传钟

（1.海南师范大学 数 学与统计学院，海南 海 口 5 71158；2.北京师范大学 香 港浸会大学联合国际学院理工科技学部，广东 珠 海519085）

随机圆覆盖面积的统计分布

汪文俊1，2，陈 传钟1

（1.海南师范大学 数 学与统计学院，海南 海 口 5 71158；2.北京师范大学 香 港浸会大学联合国际学院理工科技学部，广东 珠 海519085）

用数论方法解决单位正方形的覆盖问题.用单位正方形的均匀布点方法估计覆盖面积的均值，方差及其分布函数.

数论方法；均匀设计；Beta分布

王元和方开泰［1］首次将数论方法用于研究毁伤面积的统计分布，令 K ={（x；y）∶x2+y2≤ 1 }，圆心为O=（0，0）′，设有m个随机圆将K毁伤（或覆盖），它们的半径分别为 r1，…，rm，（0 ＜ ri＜ 1；i=1，…，m），其圆心 O1，…，Om，相互独立且服从二维正态分布

来估计.文[1]讨论了在K上如何布N个点的问题，提出了四种方法，并指出四种方法的优劣.最近，王元和方开泰［2］从数论中的“圆问题”的出发，进一步比较了四种方法，指出方法Ⅲ和方法Ⅳ有相同阶的精度.周永道和方开泰［3］详细比较了m=2时理论的结果和随机模拟的表现，给出了更为细致的分析.

在实际问题中，被覆盖的不一定是单位圆K，可能是单位正方形H=[0，1]2，H被m个随机圆覆盖的面积S的统计分布在实用中十分重要，这就是本文的研究目的.设Sm表示单位正方形H被m个随机圆覆盖的区域

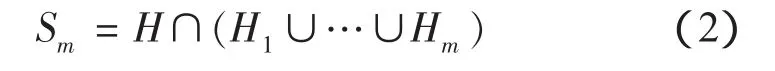
图2给出m=2的覆盖情形.图中斜线部分表示覆盖区域Sm，记面积为S，S是一随机变量.本文主要研究S的均值，方差及分布.

采用统计模拟来求S的均值，方差及分布，其方法如下：设在单位正方形H上均匀分布N个点{（xi，yi），1≤i≤N}，用这些点代表H.然后用Monte Carlo法产生 m 个中心，从而获得m个随机圆H1…Hm.用M表示单位正方形H上N个点被这m个随机圆覆盖的点数，则S的估计为

1 覆盖面积分布的研究

数论方法的实质是在s维的单位区域Cs能够找到均匀分散的点集合，在几何概率的随机模拟中，NT网起了关键性作用.构造NT网的方法很多，如好格子点方法（good lattice point method），好点法（good point method），Halton方法以及 H ammeisley方法，详见Fang and Wang［4］.本文的随机模拟采用了好格子点法，其做法如下：（n；h1，…，hs）是一整数向量，满足1≤ h1＜n，且hi和n的最大公约数为1，则

Pn=xk= （xk1，…，xks），由向量（n；h1，…，hs）生成的好格子点，在更多的文献中，往往直接利用xk=（xk1/n，…，xks/n）k=1，…，n 生成得到，此文中亦用此方法，用N=10 946个点来组成一个NT网.

覆盖面积S的分布显然会受到随机圆的半径（r1，…，rm）和方差的影响.考虑 0 .5 ＜ ri≤1，0 ≤＜ 1，（i=1， …，m）.为了有效的显现这些参数对S的影响，我们采用均匀设计［1，5］U20（204）和 U20（2010）来安排（r1，r2，，）和（r1，…，r5，，…，σ25）的变化组合，详见表1和表2.对每种情形（m=2，5），随机模拟 r =5 000 次，并计算 5 000 个S^的均值和方差，分别列于表1和表2的最后两列.用 Mn和 Vn作因变量，（r1，…，rm）和（，…，）作自变量，运用二次回归多项式的建模技术，得

表1 均匀设计U20(204)及试验结果Tab.1 Uniform Design U20（204） and the results

利用建模回归技术，同时考虑变量选择，研究期望 Mn与 r1，…，rm关系时，发现当取对数得到的模型更佳.两个模型的确定性系数分别是，检验的F值为F1=312.160，F2=42.538，模型是显著的.从模型中观察到S的期望与 ri，（i=1，2）正相关，与，（i=1，2）负相关，即随机圆的半径越大，其覆盖面积越多；圆心越靠近单位正方形的中心，其覆盖部分越大.S的方差与ri与（i=1，2）正相关.

由于S的值在[0，1]中，直观上可试用Beta分布来拟合，Beta分布的密度函数由两个参数α＞0，β＞0来决定

式中 B（α，β）为数学中著名的 Beta函数.若 X～B（α，β），则

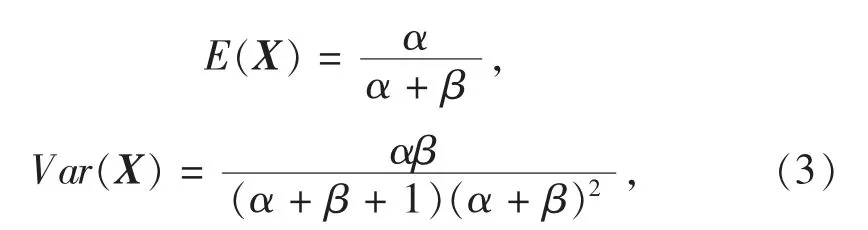
有关Beta分布的详细讨论可参见方开泰，许建伦［6］.图3 给出了第 4 ，9，11，12，13，20 个六个参数组合下的Beta分布的q-q图，明显看到Beta分布可以很好的拟合S，但从q-q图发现当m=2时，即用两个随机圆去覆盖时，两端拟合的并不是太好，主要可能是半径r1，r2较小，或是，较大，覆盖面积小的缘故.同时在进行Beta分布拟合，选择α，β时，由Beta分布性质可知（文[6]），若随机变量服从参数为（α，β）的 β 分布，则其均值和方差如（3）式，对每个试验点的5 000次抽样，可得参数α，β的矩估计，k阶样本矩定义为

由（4）解得α，β的矩估计如下：

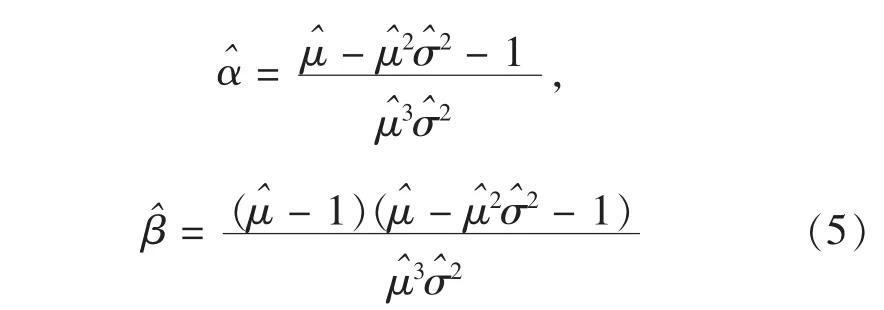
图3中的a，b即为矩估计方法估计得到的α，β值.

当 m =5 时，应用表2中均匀设计 U20（202×5）同样进行拟合，得到的期望Mn和方差Vn列在表2中最后两列，与表1中的数据进行比较，明显看到，随着随机覆盖圆数目的增多，其S的期望变大，方差变小.另一方面，期望 Mn，方差 Vn与参数（ri，，i=1，…，5）建立模型，其mean依然是与半径ri正相关，与负相关；方差和半径 ri，正相关.最后对于每种试验组合的5 000次S的估计值，Beta分布仍表现出很好的拟合效果，如图4所示的Beta分布的q-q图，看到图中两端也都拟合的相当好，即此种情形下各个数据都可以很好的用Beta分布拟合.随机圆的个数m=3，4时，其结果类似，故不再详细说明.

表2 均匀设计U20（2010）及试验结果Tab.2 Uniform Design U20(2010)and the results

3 结论

以上分析我们可以得到，覆盖面积S近似服从Beta分布，并且当随机圆的个数增加时，拟合效果会更好.同时，当m固定，随机圆的半径ri，（i=1，…，m）增大时，S 的均值增大，方差减小；σi，（i=1，…，m）减小时，覆盖面积S的均值增大，方差减小.

感谢：本文得到方开泰教授的指导，陈传钟教授的支持，得到BNU-HKBU联合国际学院的资助.

［1］Wang Y,Fang K T.Number theoretic Methods in applied statistics[J].Chin Ann Math,1990,11B,41-55.

［2］王元,方开泰.统计模拟中的数论方法[J].中国科学A,2009,39(7):1-8.

［3］周永道,方开泰.覆盖单位圆的序贯方法[J].数理统计与管理，(2010),将发表.

［4］Fang K T,Wang Y.Number-theoretic Methods in Statistics[J].Chapman and Hall,1994.

［5］方开泰.均匀设计-数论方法在试验设计中的应用[J].应用数学学报,1980,3(4):363-372.

［6］方开泰,许建伦.统计分布[M].科学出版社,1987.

责任编辑：毕和平

The Statistical Distribution of Random Round Coverage

WANG Wenjun1，2， CHEN Chuanzhong1
（1.College of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China；2.Division of Science and Technology，BNU-HKBU United International College，Zhuhai 519085，China）

In this paper,number theoretic method is used to solve a practical problem,i.e.,the cover-age problem of unit square.The uniform design in unit square is used to estimate the mean,variance and distribution of coverage area S.

number theoretic method；uniform design；Beta-distribution

O 212.1

A

1674-4942（2010）03-0237-05

2010-06-17