基于相关系数法的数控机床评价模型
杨明川 王春秀
(宁夏大学机械工程学院,宁夏银川 750021)
基于相关系数法的数控机床评价模型
杨明川 王春秀
(宁夏大学机械工程学院,宁夏银川 750021)
针对数控机床故障间隔时间分布模型的参数精度不高且不方便计算的问题,基于相关系数法利用Matlab编程来估计数控机床威布尔分布的三个参数,使其既符合精度要求,又易于实现。
数控机床 相关系数法 三参数威布尔分布 Matlab
现在数控机床可靠性的要求越来越高,在可靠性评价之前,需要建立数控机床的可靠性模型。常用的可靠性模型有威布尔分布模型和指数分布模型。指数分布模型认为机床在某一时刻的可靠度与之前的运行时间无关。威布尔分布由“最弱环节模型”推导而出。“最弱环节模型”认为系统、设备等产品的故障起因于其构成元件中最弱元件的故障,这相当于构成链条的各环节中最弱的链节寿命决定了整个链条的寿命。由此可见威布尔分布模型比指数分布模型更加符合实际情况。本文以5台某系列数控机床半年的26个定时截尾故障数据为例给出具体计算过程。
1 数控机床故障间隔时间的寿命分布模型
根据某数控机床厂提供的数控机床故障间隔时间的历史记录来拟合其概率密度函数。本文共采集了5台国产数控车床的现场故障信息,其具体数据如下表1所示。
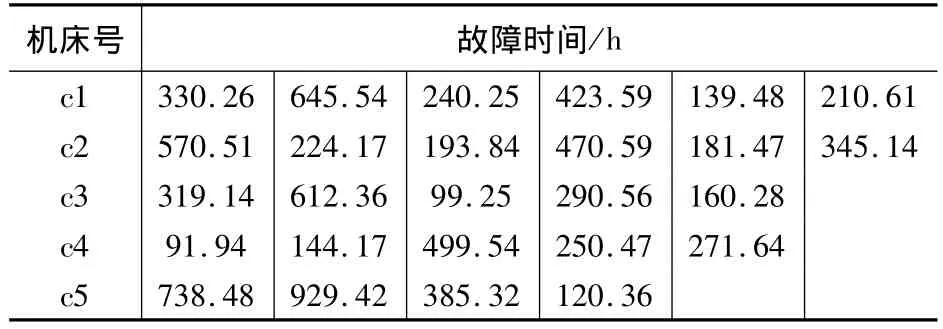
表1 某数控机床故障间隔数据
将故障间隔时间的观测值 t∈[91.94,929.42]分为6组,其组间距为139.67,如表2所示。
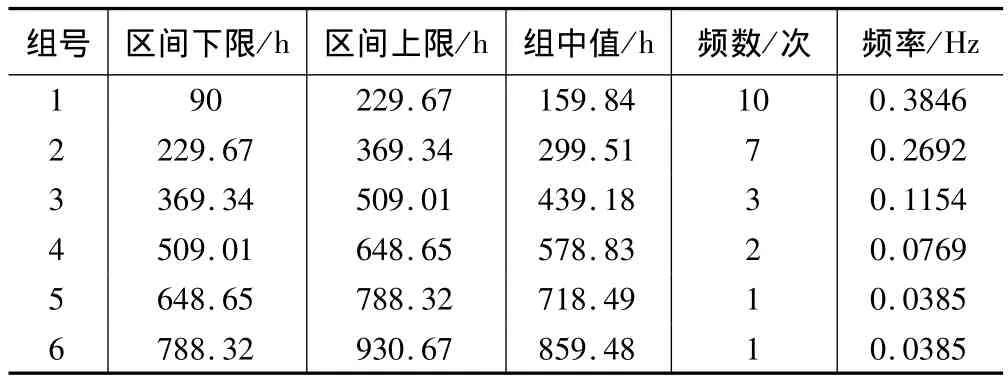
表2 故障时间和频率
以上面六组数据的组中值为横坐标,故障的频率为纵坐标,绘制故障间隔时间散点图[3],如图1。
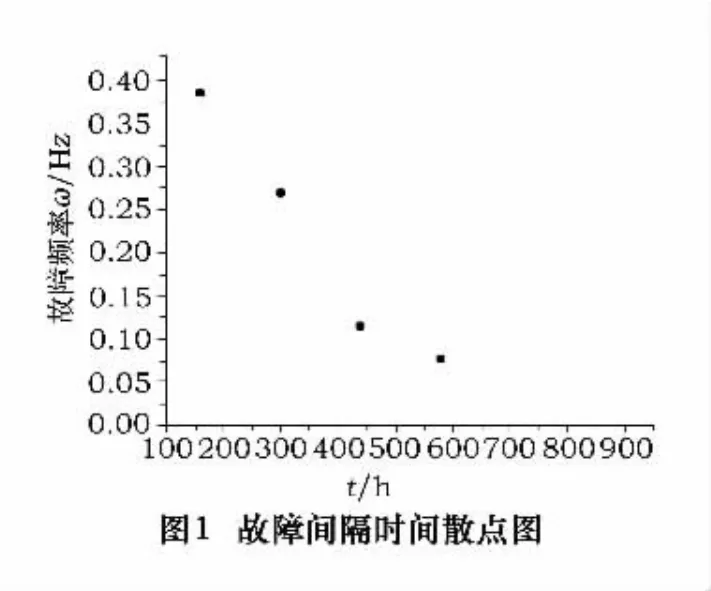
由图1可知,故障概率密度曲线呈单调下降趋势,故障间隔时间分布不会是正态分布或对数正态分布,而有可能是指数分布或者威布尔分布。
2 威布尔分布参数估计
三参数威布尔分布包含形状参数m,位置参数γ和尺度参数t0。由于位置参数不容易估计,所以传统方法将威布尔分布的三分布参数转换为两分布参数,仅对形状参数和尺度参数估计[1]。固然给计算带来了一定的方便,但是由于其没有考虑位置参数的特性,决定了计算值与实际值之间会出现较大的误差。而采用极大似然估计法可以求解三个参数并且有较高的精度,但是需要解三个超越方程并且其计算过于麻烦。针对这一问题,本文采用相关系数法,先计算其位置参数再计算形状参数和尺度参数[2]。进而得出三参数威布尔分布模型,这可以提高数控机床可靠性分析与评价的精确性。
2.1 相关系数法估计的理论
当威布尔分布的形状参数等于1时,便转化为指数分布。即威布尔分布包含了指数分布[3],因此可以认为故障概率密度函数服从威布尔分布。为了得到准确的模型,本文先估计其位置参数。
三参数威布尔分布的累积失效概率函数计算公式[4]如下所示
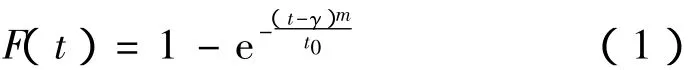
式(1)中:m 为形状参数,m >0;γ 为位置参数,γ >0;t0为尺度参数,t0>0;t为产品寿命,t≤γ;F(t)为累积失效概率分布函数,0≤F(t)≤l
对式(l)进行等价变形处理,可得下式
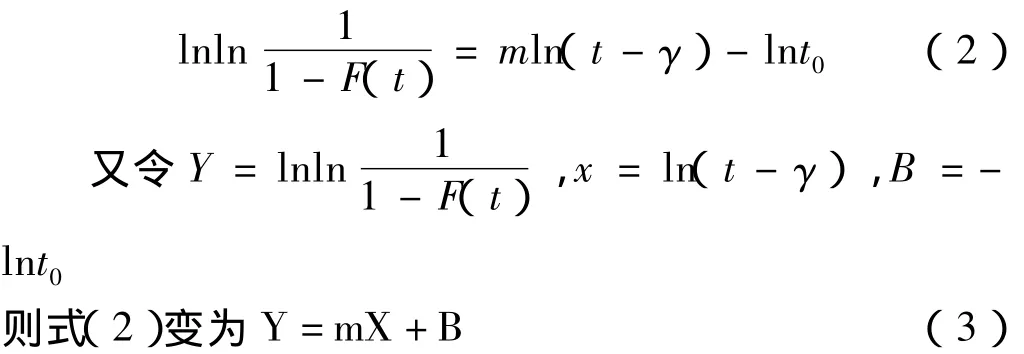
式(3)所表示的是等分度平面坐标系x-y中的一条斜率为m,截距为B的直线方程即回归直线。对于三参数威布尔分布,当位置参数γ已知时,就可以利用回归分析通过最小二乘法求出其m和t0的估计值;若位置参数γ未知则需要先求出γ的值再估计m和t0的值。本文就基于这种情况进行分析。由式(3)可知,当γ估计正确时,X与Y存在线性关系。将其在威布尔概率纸上描点表现为各点近似分布在一条直线上,可以通过最小二乘法求解m和t0;反之则X与Y之间就不存在这种线性关系。当^γ逐渐增加时,相关系数R逐渐增加;当^γ达其理论值γ时,R也达到它的最大值[5],此时x与Y成线性关系;当^γ进一步增大时,R又逐渐减小。由此可见,只要求出相关系数R最大时的^γ,就是位置参数的最佳估计值。
2.2 用相关系数法估计其位置参数的方法
从上述可知,求位置参数γ的最佳估计值的过程就是求相关系数R最大值的过程。根据高等数学求极大值的方法,只需求出相关系数R对γ的一阶导数,并令其等于零,然后解方程即可。此时求出的^γ就是R最大时的位置参数的最佳估计值^γ[6]。
对于容量为n且服从威布尔分布的数控机床故障间隔时间,将其数据观测值按从小到大的顺序依次排列,对应的样本分布函数用F(ti)表示,则有

对于威布尔分布恒有R>0,故求R对γ的一阶导数与求R2对γ的一阶导数对求γ而言是等价的。为简化算式,这里计算R2对γ的一阶导数。按照高等数学求导公式对其求导并进行化简得
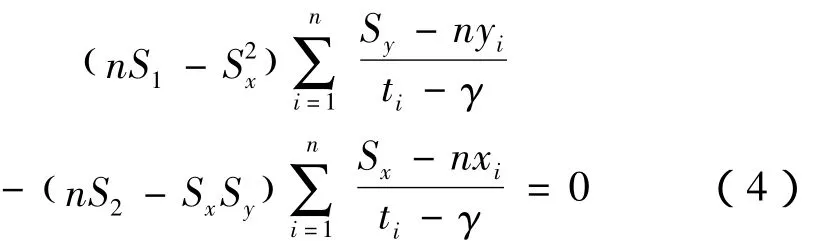
于是求解γ的方程已经给出。式(4)所包含的仅有一个未知量,γ完全可以求出。与极大似然法求解三个复杂的方程,并且进行迭代相比减少了大量的运算。
3 相关系数法估计在威布尔分布中的应用
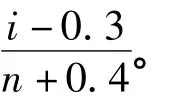
3.1 编制M文件
首先根据二分法[7]编制M文件保存在Matlab的默认路径当中,以便以后调用。下面是程序代码:
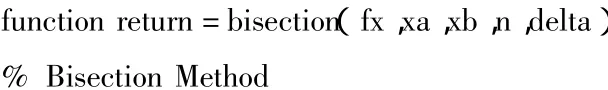
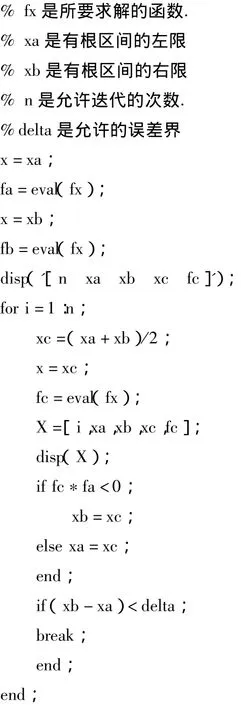
3.2 编制主函数文件
分别计算其方程中的各个值如下所示。

3.3 计算位置参数
有根区间的左右限是根据其位置参数的图估法计算[3]得出来的。
用bisection(f,0,100,20,10^(-3))计算其参数得出结果为69.98。
3.4 计算其形状参数和尺度参数
由于其计算出来的γ>0,所以对其三参数威布尔分布进行的变换为t′=t-γ,由此可将其变换为二参数威布尔分布。其数据在直角坐标系中符合直线分布,变换后的数据可根据最小二乘法原理进行计算。用Matlab编写的具体程序如下:其中t为观测数据,t1为变换后数据


4 威布尔的拟合度检验
对于数控机床故障概率密度函数的分布要进行拟合优度检验,这里选用K-S检验(柯尔莫哥洛夫-斯米尔诺夫检验)法[3]。将n个(这里是26个)故障时间数据按由小到大的次序排列,根据假设的分布,计算每个数据ti对应的故障概率函数F(ti)。将其与经验分布函数Fn(ti)进行比较,其中差值的最大绝对值即检验统计量Dn的观察值。将Dn与临界值Dan进行比较,满足下列条件,则接受原假设,否则拒绝原假设。
原假设 H0:参数的值服从 m=1.316 1,γ =69.98,η=292.94的三参数威布尔分布。
列表计算理论分布和经验分布的差异度,如表3所示。
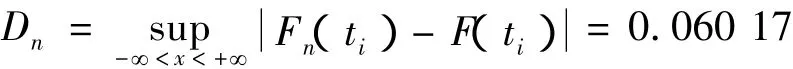
这样Dn<,原假设成立,既数控机床的参数值符合 m=1.316 1,γ =69.98,t0=1 764.12 的三参数威布尔分布。
5 故障间隔时间概率密度函数与分布函数的确定
数控机床的故障间隔时间概率密度函数为
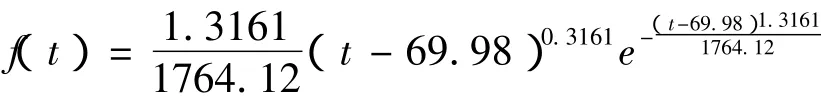
数控机床的分布函数为
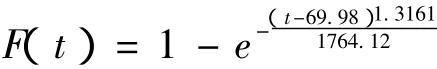
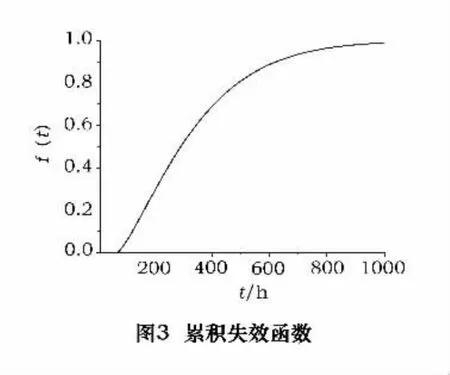
f(t)和F(t)的曲线分别如图2和图3所示。
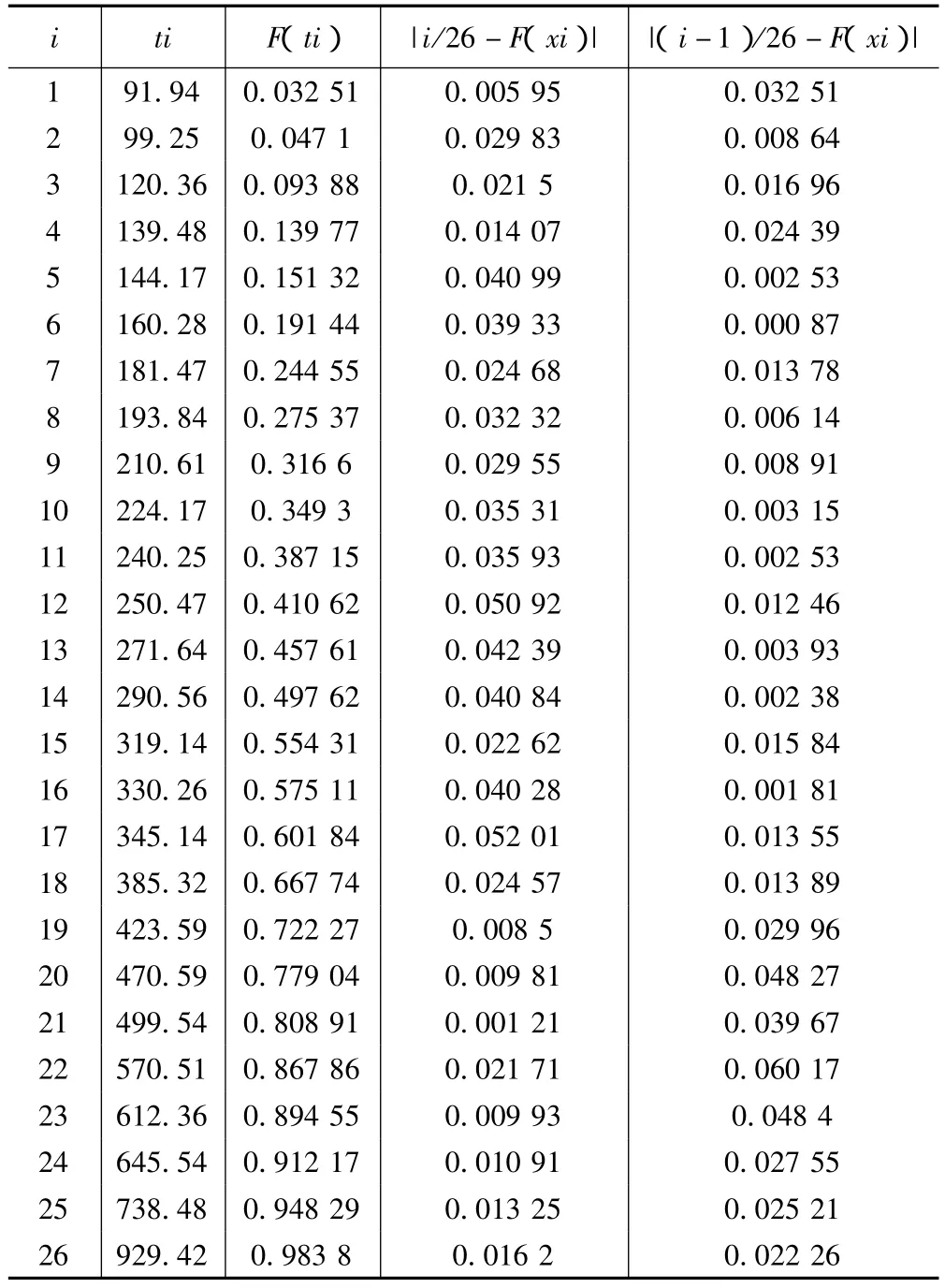
表3 数控机床的K-S检验计算
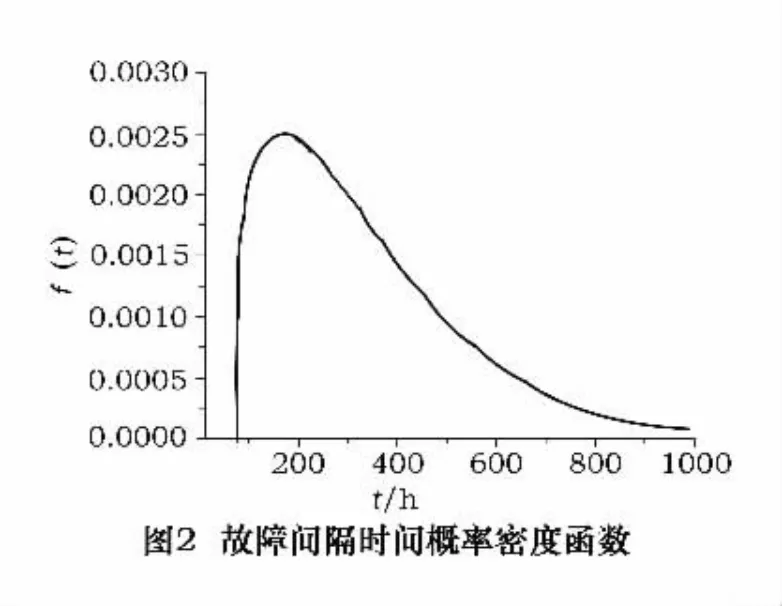
布尔分布用上述计算方法得出形状参数为1.923 4,尺度参数为92 116,数控机床的故障间隔时间概率密度函数为
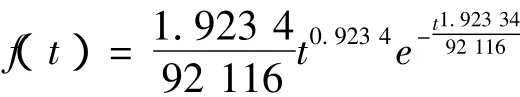
6 寿命分布模型的分析
从图3可以看出,数控机床在早期故障率高发期运行时间过长,在偶然故障阶段运行时间过短,这是国产数控机床可靠性不高的重要原因。因此提高可靠度应缩短早期故障期,并尽量延长偶然故障阶段。
早期故障出现在产品开始工作的初期,在此阶段,故障率高,可靠性低,但随工作时间的增加而迅速下降。数控机床发生早期故障的原因主要是由于设计、制造工艺上的缺陷,或者是由于零件和材料的结构缺陷所致。因此要缩短此故障期就应该在出厂前进行相应的试验,尽可能的减少早期故障次数,根据其位置参数可以合理制定早期故障排除试验时间。
偶然故障期是数控机床的正常工作期,其特点是故障率比早期故障率小得多,近似为一常数。这个时期的故障是由偶然不确定因素所引起的,故障发生的时间也是随机的,所以不同的厂家会有不同的原因,要提高其可靠度就应该到使用方进行详细调研,根据其反馈进行具体的分析。
7 结语
(1)采用三参数威布尔分布模型进行分析更加符合实际工作环境,可以得出更精确的数控机床可靠性的各个参数,为数控机床可靠性的提高和可靠性的增长奠定分析基础。
(2)结合其工程实际和精度要求,给出了估计数控机床三参数威布尔分布的方法。
(3)为提高数控机床可靠性,减少其早期故障时间提供理论支持。
1 张英芝,申桂香,吴甦等.随机截尾数控机床三参数威布尔分布模型.吉林大学学报,2009(3)
2 严晓东,马翔,郑荣跃等.三参数威布尔分布参数估计方法比较.宁波大学学报,2005(9)
3 贺国芳.可靠性数据的收集与分析.北京:国防工业出版社,1995(12)
4 刘惟信.机械可靠性设计.北京:清华大学出版社,1995(2)
5 方志强,高连华.三参数威布尔分布在寿命分析中的参数估计.装甲兵工程学院学报,1999(3)
6 胡恩平,罗兴柏,刘国庆.三参数Weibull分布几种常用的参数估计方法.沈阳工业学院学报,2000(9)
7 姜健飞.数值分析及其Matlab试验.北京:科学出版社,2004(6)
如果您想发表对本文的看法,请将文章编号填入读者意见调查表中的相应位置。
Evaluation Model on NC Machine Based on Correlation Cofficient Method
YANG Mingchuan,WANG Chunxiu
(School of Mechanical Engineering,Ningxia University,Yinchuan 750021,CHN)
The parameter of NC machine MTBF method is not precise and convenient calculate.This document estimates three parameter of Weibull distribution based on the correlation cofficient using the Matlab.It causes both easy to achieve ,and to meet the accuracy requirement.
NC Machine;Correlation Cofficient Method;3 -Parameter Weibull Distribution;Matlab
杨明川,男,1984年生,硕士研究生,主要研究方向为先进制造技术。
(编辑 周富荣) (收修改稿日期:2009-08-10)
10119

