基于三角模糊数的属性层次模型分析法在工程风险评价中的应用

司马军 刘书华 刘文平

基于三角模糊数的属性层次模型分析法在工程风险评价中的应用

司马军 刘书华 刘文平

一、引言

工程项目风险评价是在风险识别和估计的基础上，把风险因素发生的概率、损失程度等因素综合考虑，得出系统发生风险的程度以及可能性，它是应用各种风险分析的技术，用定性、定量的方法或是两者相结合，来处理不确定性风险的过程。工程项目的风险评价是工程项目实施阶段风险管理对策选择的重要依据，具有关键的作用。

工程项目风险分析方法有许多种，常见的主要有专家打分法、蒙特卡罗模拟法、层次分析法等，其中专家打分法利用专家经验，对所有风险因素的重要性进行评估，再综合成系统整体风险，其优点是简便易行，但易受主观因素影响；蒙特卡罗模拟法是通过随机计算、抽样或统计试验，建立概率分析模型，分析不确定性风险因素引起的风险概率，其优点是可结合结构分析与试验，考虑因素多，但是计算量大，且只能得出最终解而无法得出过程解；层次分析法可以将复杂风险问题分解为若干层次和要素，通过比较、判断和计算，得到它们的重要程度，最后合成整个项目风险，其优点是方法简单、灵活，但易受主观因素的影响。

由于人们对工程项目风险的认识具有主观意识性，对其风险的形成因素不完全明确，对这些因素之间的关系不完全清楚，因而工程项目风险的评价体系是一个典型的模糊系统。如果完全用数学公式推导来进行工程项目风险的评价，与事实难以吻合；如果单凭主观判断来评价，又缺乏科学依据。因此，将模糊数学理论运用于风险评价，为决策者提供科学可靠的依据，是一种行之有效的评估方法。

二、基本原理

1.属性层次模型基本原理

本文所采用的属性层次模型（AnalyticHierarchicalModel，简称 AHM）源于层次分析法（AHP），AHP是一种多准则决策方法。其将定性分析和定量分析相结合，根据问题的性质和所求的总目标，将问题分解成不同的组成因素，并按照因素间的相互关联影响以及隶属关系，根据不同层次聚合组合，组成一个多层次的分析结构模型。

利用AHP法处理问题时关键在于构造两两比较的判断矩阵且使所构造的判断矩阵符合一致性检验要求；但是由于构成因素的复杂性，往往对判断矩阵的一致性检验比较困难。而属性层次模型可以较有效地解决无结构决策问题，与AHP相比，AHM最大的优势就是其两两比较测度矩阵不存在“一致性检验问题”。AHM的两两比较测度矩阵可通过AHP中判断矩阵转换得到。这样利用AHM测度判断矩阵就可以计算出各指标的权重值。具体过程如下：

设 C为一个准则，u1，u2，……，um为n个元素，对于准则C，比较两个不同元素ui和uj（i≠j），ui和uj对准则C的相对重要性分别记为uij和uji。

按属性测度的要求：uij和uji满足

则由相对属性uij组成的n阶矩阵A=（uij）称为属性判断矩阵。相对属性uij可由比例标度aij确定，通常由下式给定：

其中k为大于2的正整数，β≥1，β 值通常取 1或者 2，本文取β=2。

比例标度由AHP方法中的1-9评判准则确定。

属性判断矩阵相对权重可表示为表2：

表1 1-9评判准则

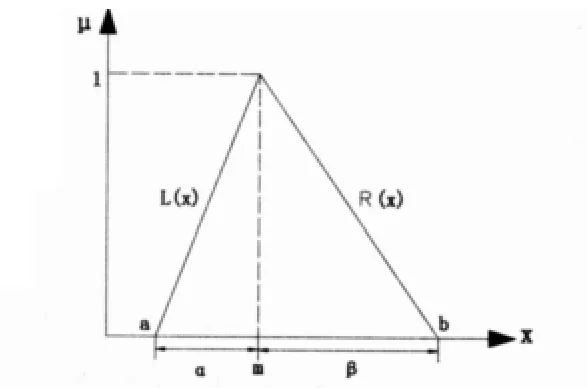
图1 三角模糊数隶属函数表示方法

2.三角模糊数

（1）三角模糊数的基本概念

定义，设M∈F（R）为一个模糊数。

①存在 x0∈R，使得 μM（x0）=1

②对任意 α∈[0，1]，Aα=[x，μAα≥α]，是一个闭区间。这里F（R）为所有的模糊数集；R为实数集。

图1给出了三角模糊数隶属函数表示方法，由图1可知，线性三角模糊数可由模糊数三元组表示（m-α，m，m+β），令a=m-α，b=m+β，则模糊数记为：M=（a，m，b）

（2）三角模糊数的计算法则及清晰化处理

设2个三角模糊数为M1和M2，M1=（a1，m1，b1），M2=（a2，m2，b2）则其加减运算法则如下：

①三角模糊数加法

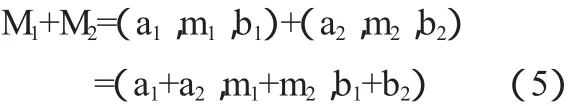
②三角模糊数减法

将模糊数转化为一个确定量，即模糊数的清晰化，本文采用的是一阶零点矩法，一阶零点矩法的数学表达式为：

三角形模糊数应用一阶零点矩法清晰化处理数学表达式为：

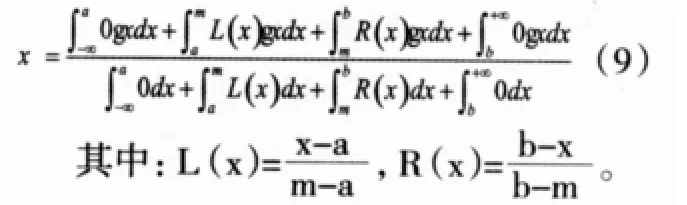
三、算例

某引水供水工程，输水线路设计全长97km,其中隧洞全长约87km，有10%左右的隧洞处在不稳定围岩地段，成洞条件差。输水线路北段和南段地震基本烈度为Ⅶ和Ⅷ度。沿线根据不同的地形、地质和水文条件布置有倒吸虹等建筑物。

该输水工程线路长，地形地质水文条件复杂。在工程设计、施工及运行管理中会遇到众多的风险因素影响。因此对这些风险因素进行全面、准确的评价，在工程建设风险管理中有十分重要的意义。

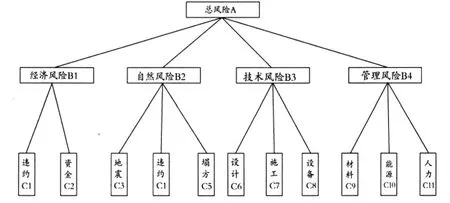
图2 风险类别层次结构图

表3 A-B判断矩阵

表4A-BAHM判断矩阵

表5B3-CAHM判断矩阵

表6 因素层权重集合

根据该工程的具体情况，本文在运用AHM法时，把层次构造定为三层。最高层准则为总风险度评价。第二层为工程风险分类，一般有经济风险、自然风险、技术风险、管理风险等。第三层为结构的最底层，包括各风险类别中具体风险因素。上述层次结构如图2所示。

采用AHM法计算指标权重。首先构造基于三角模糊数的A-B判断矩阵（见表3），根据公式（9）将模糊数清晰化处理，并计算各指标相对属性权wcuj（见表4）。

同理，根据专家提供的指标相对重要性，将其清晰化处理并构造属性判断矩阵，计算各指标相对属性权wcuj,这里以B3-CAHM判断矩阵为例，计算结果见表5。

将各个子风险因素进行排序（见表6），从表6中可以看出，经济风险中的资金因素占权重最大为0.3821，其次为自然风险中的地震因素所占权重0.1766以及技术风险中的施工因素0.1164，根据分析评估结果，我们可以采取加强资金管理，地质勘探和加强施工技术方案论证这几项措施进行有效的风险减免。同时在施工过程中可以把加强现场管理和加强人员技术培训作为辅助措施。

当然，工程风险会随时空变化而变化，通过对工程风险灵敏度分析，动态地掌握工程风险状态，进而对风险元素进行有效控制，使之降低到最小程度也是十分重要的。

四、结语

应用属性层次模型方法对工程风险进行定量划分，并在运用专家知识经验的基础上，用模糊数学的方法避免了评价过程中的单纯主观臆断和片面性，有利于将定性分析定量化，提高了决策的科学性和准确性，实践证明这种方法应用于工程项目风险评价是科学可行的

河南省水利科学研究院 450000 固始县鲇鱼山水库胡族灌区管理所 465200 驻马店市水利工程局 463000）