基于VOF方法的造波、消波技术

兰雅梅, 郭文华, 宋秋红, 袁军亭

(1.上海海洋大学,上海 201306;2.上海河口海岸科学研究中心,上海 201201)

基于VOF方法的造波、消波技术

兰雅梅1,2, 郭文华2, 宋秋红1, 袁军亭1

(1.上海海洋大学,上海 201306;2.上海河口海岸科学研究中心,上海 201201)

以 N-S方程为控制方程,基于有限体积法,将入射波波场作为人工的分布源项加入动量方程,提出了适用于VOF方法的源造波——消波段技术,可以有效地消除波浪遇结构物的反射波;在水槽末端布设消波段吸收入射波,允许在较小的计算域内提供任意的有效工作时间,提高了计算效率。对行波及驻波的计算,分别考察了前端及末端消波段的有效性。

VOF;源造波法;Fluent

Abstract:Based on the finite volume method,the Navier-Stokes equations are used as the governing equations to develop a new module of the wave generating and absorbing function.The wave generating is introduced as the man-made source terms into the momentum equations,which is suitable for the volume of fluid method(VOF).Within the numerical wave flume,the reflected waves from the construction could be absorbed effectively.The absorbing section arranged at the end of the wave flume to absorb the incident wave,which allows for random and effective working time within the reletively smaller computation domain.Consequently,the computation efficiency is greatly improved.Finally,the validity of the absorbing section arranged at the front and end of the wave flume is investigated individually.

Key words:VOF;wave generating;Fluent

0 引言

过去的几十年里,随着计算机性能的不断提升,对数值水槽的研究取得了很大的进展。在基于 N-S方程的波浪水槽中进行数值模拟时,准确捕捉自由表面的大变形运动是关键,VOF是目前处理带有复杂自由表面问题较为理想的方法,现已被广泛应用到许多有关自由面流的流场分析中。

造波和无反射开边界的实现是建立数值波浪水池的两个关键问题。基于计算时间及计算量的考虑,要尽量缩小计算域,可将边界设置成透浪的开敞边界,这对减小水槽的有效长度是很有意义的。Arai et al.[1]在水槽末端布设速度衰减区,采用指数形式对垂向速度进行衰减;刘海青和赵子丹[2]在入射边界附近也布设速度衰减区,吸收到达入射边界处的反射波;Larsen&Dancy提出了所谓的源造波方法;高学平[3]等对驻波计算结果表明,线源造波方法能很好地吸收波浪遇建筑物产生的反射波;Wei et al.[4]将最初的线源造波改进的为空间分布的源函数造波方法,并应用于求解Boussinesq方程的非交错网格模型;Lin&Liu[5]将矩形区域内分布的质量源项添加在连续方程中,模拟了规则波(包括线性波、Stokes波、孤立波等)及不规则波。

本文基于商业化软件FLUENT,以RANS方程为控制方程,基于有限体积法,将入射波波场作为人工的分布源项加入动量方程,应用改进的空间分布的源函数方法,提出了一种适用于VOF方法的造波——消波段技术。此方法只需将入射波波场作为人工的分布源项加入动量方程,通过FLUENT软件中的接口,编写程序可方便实现此项功能,经验证可模拟二维波动场,是一种简单有效的方法。

1 理论基础

根据源造波理论,可通过在动量方程中添加源项达到造波及消波目的。将数值波浪水槽按照功能不同划分为四个区域,如图1所示,由左至右依次为:造波区、前端消波区、计算域、末端消波区。前端消波区吸收计算域内结构物的反射波;末端消波区吸收经过计算域的透射波。由于各区域功能不同,波动场及加权函数C的表达有所不同,分别为

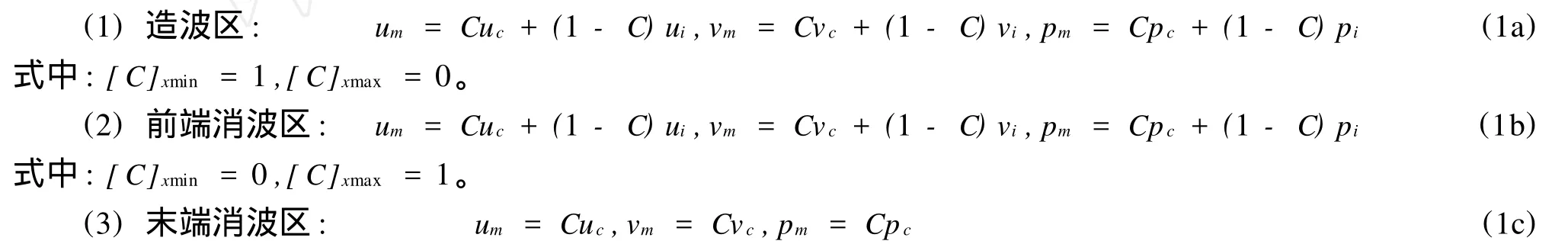
式中:[C]xmin=1,[C]xmax=0。

式(1a)～(1c)中:u、v分别为 x、y方向的速度分量;p为压强;下标m代表经过造波与消波后的流场值;下标c代表造波与消波前的流场值;下标i代表添加的来波值;C=C(x)为与空间位置有关的光滑过渡的加权函数。

由于造波区、前端消波区、末端消波区的波动场所对应的加权函数C的表达不同,使得添加在各自区域动量方程中的源项有所不同。以下以造波区为例,选择不考虑粘性作用的欧拉方程推求该区域源项的表达式。

图1 数值波浪水槽分区设置示意图

式中:ρ为流体密度;g为重力加速度;Fx、Fy分别为x、y方向的附加源项。设经过造波与消波后的速度场与压强场参见前式(1a),以 x方向为例,将添加源项及未添加源项的动量方程分别离散为

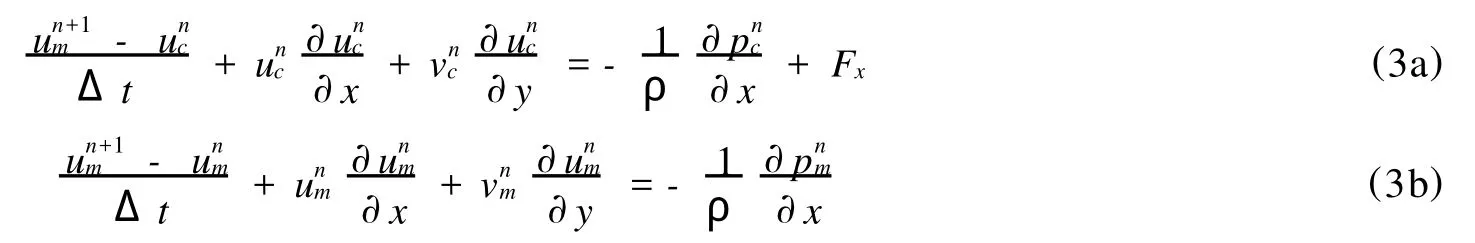
式中:上标 n+1、n分别代表n+1、n时刻的流场值。将式(1a)分别代入方程(3a)、(3b),联立求解可得

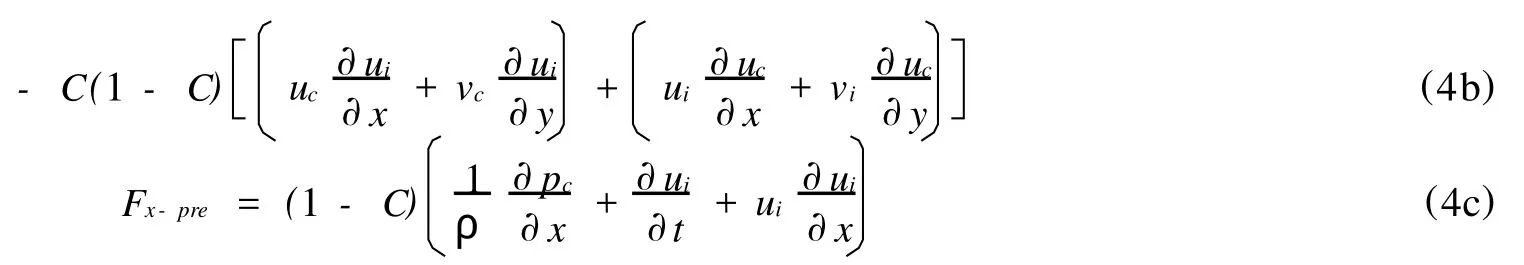
同理,可得 y方向的源项Fy的表达式。其中方程(4a)～(4c)的变量上标均为n,即代表n时刻的流场值,为简便起见,均省略未注。以此类推,按照与推求造波区源项相同的方法,根据式(1b)、(1c)可分别得到诸如式(4a)～(4c)的前端消波区、末端消波区的源项表达,然后采用UDF(用户自定义)程序,通过 FLUEN T软件中的接口,在上述三个区域的动量方程中添加对应源项即可达到模拟造波、消波目的。

2 数值模型

2.1 控制方程

由于波浪与位于浪溅区的结构物底面的相互作用,会造成波浪的破碎,出现水质点运动的紊动掺混现象,因而需要考虑湍流的影响。FLUENT(v6.2)软件采用近年来应用十分广泛的标准k-ε湍流模型,通过建立湍流脉动量与时均量之间的联系来封闭雷诺方程。不可压缩粘性流体动量方程为

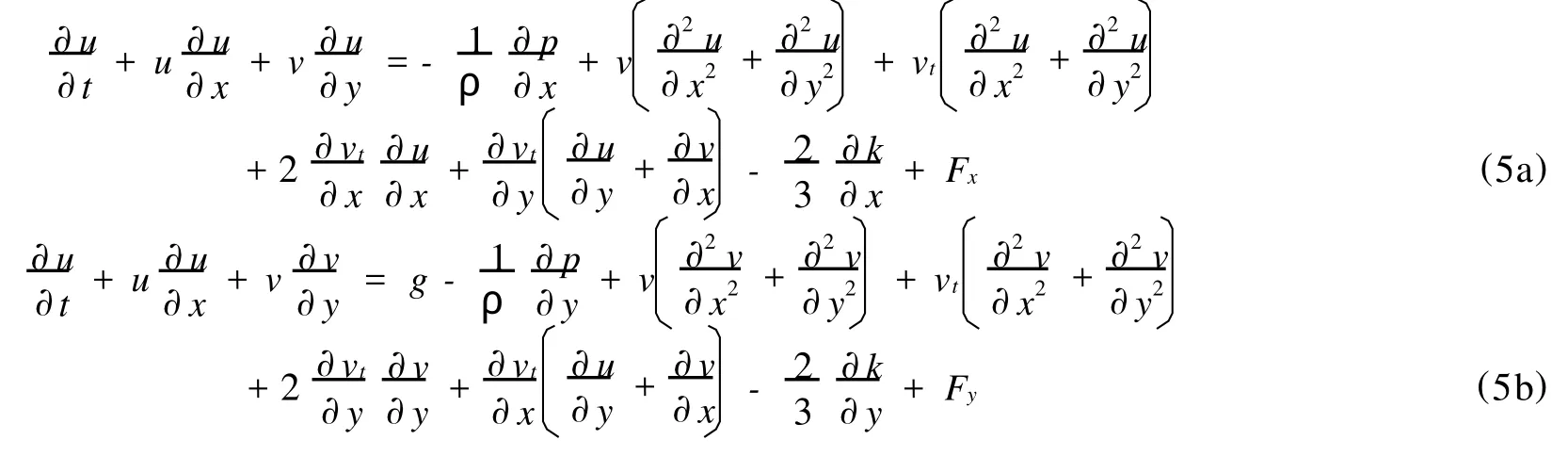
连续性方程为

湍动能k方程为

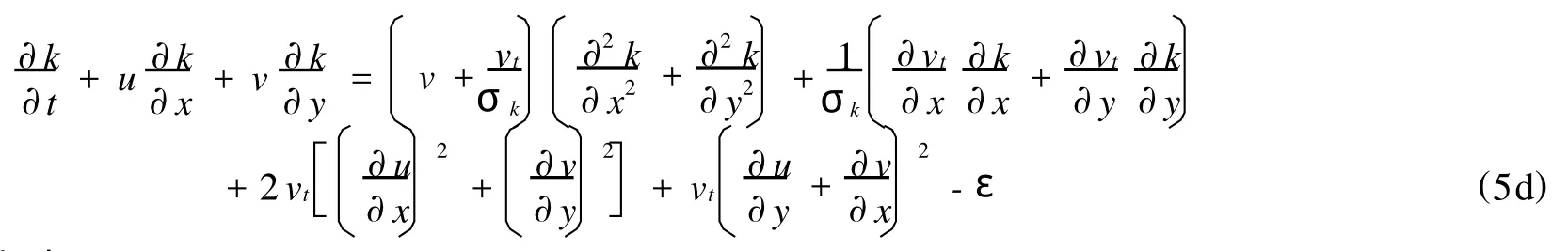
湍动能耗散率ε方程为

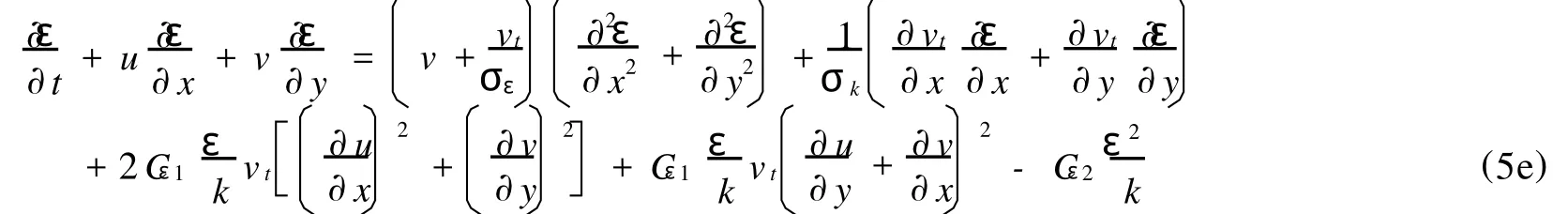
自由表面的标记采用流体体积函数方法。体积函数θ定义为单元内流体所占有体积与该单元体积之比。由定义可知,若单元被流体充满,θ值为1,空单元的θ值为0,θ值介于0～1之间表示该单元被流体部分占有。θ的方程为

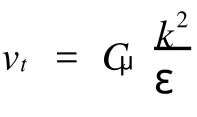
2.2 边界条件及初始条件

数值水槽的水底、顶部、左端边界及右端边界均采用对称边界条件,即壁面流体的法向速度为零。

数值水槽中,包括水、气两相,计算开始时在垂向上确定各相所占的区域,将水所在区域的体积函数θ的初始值设为1,其余区域设为0。该模型由静水状态开始造波,故流场中其他各物理量的初始值均取为零。

2.3 数值算法

气液两相流的模型选用VOF模型,湍流模型选用标准的 k-ε双方程模型,求解二维时均雷诺 N-S方程(RANS)。采用邻近修正 PISO算法求解压强-速度耦合,加快收敛速度,节省运算量。壁面附近采用标准壁面函数方法处理。

3 数值结果分析

为检验本文所建立的二维数值水槽造波的准确性及消波的有效性,给出了验证算例,水槽长度方向网格步长取Δx=L/80,高度方向静水面附近网格较密Δy=H/30,时间步长Δt=T/1 000。

3.1 非线性行波

利用图1所示水槽生成非线性行波,水深 d=10 m,波高 H=1 m,周期 T=5 s,水槽长取5.5倍波长,计算域两侧的消波区均取1.5倍波长,主要考察末端消波区的消波效率。

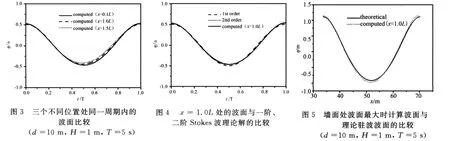
图2给出了计算域 x=0.1L、1.0L、1.5L三个不同位置处波面随时间的变化过程,其中L为波长,图3给出上述三个位置在一个周期内的波面比较。由计算结果图2、图3可看出,波列很快达到了稳定状态,且此后较长时间维持稳定的波面。为了进一步分析,将一个周期内的稳定波面与一阶、二阶Stokes波理论解进行对比,见图4。可看出,本文模拟得到的波面与理论解接近,与二阶Stokes波形更加吻合。计算表明,末端消波区对非线性波浪的吸收效果较好,此造波-消波方法能产生较理想的非线性行波。

图2 三个不同位置处的波面时间序列(d=10 m,H=1 m,T=5 s)

3.2 驻波

截去末端消波区,右端为垂直固壁,水槽长取5倍波长。如果模型正确,则由于反射波和入射波的叠加,在水槽中应该会出现驻波,且驻波的波幅为入射波的两倍,以此考察前端消波区的消波效率和造波源项和反射波之间相互影响的程度。

图5给出了一个周期内的驻波波面与三阶浅水驻波理论解的比较,可看出,得到的驻波波高为入射波波高的两倍,且与理论解基本吻合,表明前端消波区能较好地吸收波浪遇直墙形成的反射波。

4 结论

在应用VOF方法的基础上,以RANS方程为控制方程,添加了造波、消波模块。采用欧拉方程推导了造波函数源项,并将其加入动量方程,进而建立了二维数值波浪水槽。验证算例表明,即使对完全反射形成的驻波,源函数造波法能很好地吸收波浪遇建筑物产生的反射波。本文提出的用源函数造波法建立复合的造波和海绵层消波技术具有潜在的应用前景,可以方便地拓展到三维不规则波以及多向不规则波的数值模拟。

[1] Arai M,Paul U K,Cheng L-Y,Inoue Y.A technique for open boundary treatment in numerical wave tanks[J].Journal of the Society Naval Architects of Japan,1993,173:45-50.

[2] 刘海青,赵子丹.数值波浪水槽的建立与验证[J].水动力学研究与进展:A辑,1999,14(1):8-15.

[3] 高学平,曾广冬,张亚.不规则波浪数值水槽的造波和阻尼消波[J].海洋学报,2002,24(2):127-132.

[4] Wei G,Kirby J T,Sinha A.Generation of waves in Boussinesq models using a source function method[J].Coastal Engineering,1999,36:271-299.

[5] Lin P Z,Liu P L-F.Internal wave-maker for Navier-Stokes equations models[J].Journal of Waterway,Port,Coastal and Ocean Engineering,1999,125(4):207-217.

[6] Wang B L,Liu H.Higher order Boussinesq-type Equations for Water Waves on Uneven Bottom[J].Applied Mathematics and Mechanics,2005,26(6):774-784.

Wave Generating and Absorbing Based on VOF

LAN Ya-mei1,2, GUO Wen-hua2, SONG Qiu-hong1, YUAN Jun-ting1
(1.Shanghai Ocean University,Shanghai 201306,China;2.Estuarine&Coastal Science Research Center,Shanghai 201201,China)

O352

A

1001-4500(2010)01-0022-04

2009-10-08

上海高校选拔培养优秀青年教师科研专项基金(科07-52)资助项目

兰雅梅(1976-),女,博士研究生,现主要从事结构物水动力学研究。