基于ARMA模型的湖南信用服务产业发展的预测

黎振强

(湖南理工学院 经济与管理学院, 湖南 岳阳 414006)

基于ARMA模型的湖南信用服务产业发展的预测

黎振强

(湖南理工学院 经济与管理学院, 湖南 岳阳 414006)

利用ARMA模型对湖南信用服务产业未来的发展进行了预测, 得出了湖南信用服务朝阳产业的发展水平将会不断的提高, 发展前途光明的结论.

ARMA模型; 信用服务产业; 预测

Abstract:The paper predicted the future development of the credit services industry in Hunan through ARMA model and got the conclusion that the credit services sunrise industry in Hunan will continue to increase the level of development and have a bright future.

Key words:ARMA model; credit services industry; forecast

引言

信用服务产业可以界定为专门从事信用信息采集、整理和加工, 并提供相关信用产品和服务的生产部门、企业和中介机构的总称. 信用服务产业的产生和发展是社会分工的产物, 为了降低交易风险, 市场主体需要详细了解交易对象的信用状况或为维护交易安全寻求更多的保障, 这些活动在初期是由市场主体自行完成的, 随着交易规模和交易领域的扩展及专业化分工的发展, 这样的活动逐步分离出来, 由独立的、社会化的专门机构来进行, 也就产生了信用服务机构及其产业. 黎振强, 罗能生(2009)利用主成分分析方法从宏观层面对湖南信用服务产业的发展进行了综合评价, 得出了随着湖南人均GDP的增加、市场开放度的提高、城市化水平的提升以及人们的科技文化水平的提高, 湖南信用服务产业将会不断发展的结论, 这种整体分析是非常必要的, 得出的结论也是符合湖南信用服务产业发展的经济背景的. 为了更加全面地考察湖南信用服务产业的发展, 下文从微观层面具体地预测湖南信用服务产业的发展. 鉴于信用服务产业的“朝阳性”, 数据获得性有限, 本文利用课题组调研获得的湖南中小企业信用担保数据为样本对其进行个案分析.

基于ARMA模型的湖南信用服务产业发展预测

(一) 湖南中小企业信用担保发展现状

信用担保业是一种通过承担数倍于自身资产的担保责任, 利用有限的资源, 能够引导社会资金流向、体现政府政策导向的产业, 是一种服务于债权人与债务人的中介组织, 是一把解开中小企业贷款难和银行放款难问题的新钥匙, 它的出现有利于调节微观经济活动和提高整个社会经济效益. 湖南省从1999年开始了中小企业信用担保体系建设, 最初由政府引导、全额出资在湘潭、常德等地设立了担保机构. 2002年《中小企业促进法》颁布以后, 各级政府加大了投入, 采取出资举办、参股、委托经营等方式, 扶持担保机构的建立. 同时, 鼓励民营资本进入中小企业信用担保行业, 使全省中小企业信用担保行业得到了蓬勃发展. 据本课题组调研, 截止2007年底, 全省已组建为中小企业服务的担保机构119家, 其中, 注册资本金1亿元以上的机构11家, 资本金5000万元到1亿元的机构13家, 资本金5000万元以下的机构95家; 2007年湖南全省信用担保机构资本金总额300亿元, 受担保企业2993户, 为中小企业信用担保金额45亿多元; 担保机构从业人员1109人, 其中中级以上专业技术职称的人员759人, 具有大学以上学历的人员921人. 湖南经过十余年的发展, 信用担保机构为很多中小企业的融资提供了帮助, 产生了巨大的社会经济效益. 为了对湖南未来中小企业信用担保业发展有一个准确的把握, 本文利用ARMA进行预测.

(二) 实证分析

1. 数据的预处理

ARMA模型是一种比较成熟的适于短期预测模型, 它要求时间序列是随机和平稳的, 而且需要大量数据. 但是许多经济时间序列是非平稳的, 因此我们必须将一个时间序列经过d次差分把其变成平稳的, 然后用ARMA( p, q)拟合平稳时间序列; 平稳时间序列的随机性服从一定的概率分布,我们通过模型就可以做到拟合过去的信息, 进而预测未来的信息并评价数据的质量. 本文以序列XD代表湖南中小企业信用担保的时序数据, 首先考察湖南2002年至2007年中小企业信用担保数据的平稳性. 序列的平稳性可以用自相关分析图判断, 如果序列的自相关系数很快趋于0, 即落入随机区间, 时序是平稳的, 反之非平稳. 从图1序列XD的自相关—偏自相关分析图中可看出原序列是平稳, 所以本文对原数据不做差分处理.

图1 序列XD自相关—偏自相关分析图

2. 模型的识别

ARMA一般通过考察平稳时间序列的自相关和偏自相关系数的性质来进行模型的选择. 一般而言, 如果自相关系数表现出拖尾而偏自相关系数表现出P阶截尾, 则选择AR(p)模型; 如果自相关系数表现出q阶截尾而偏自相关系数表现出拖尾, 则选择MA(q)模型; 如果自相关系数和偏自相关系数均表现出拖尾, 则选择ARMA(p, q)模型. 从图1序列XD的自相关系数和偏自相关系数来看, 本文尝试了AR(1)模型和ARMA(1,1)模型.

3. 模型参数估计

选定模型的阶数后, 进一步要计算模型的未知参数. 这里选择最小二乘法来估算参数值. 本文利用相关数据得出的AR(1)模型和ARMA(1,1)模型的参数估计结果如图2、图3.

AR(1)模型参数估计与相关检验结果为:

图2 AR(1)模型参数估计与相关检验结果

模型的选择主要参考的是赤池(AIC)和施瓦茨(SIC)信息准则, 它们的值越小, 模型拟合得越好. 通过对图2的AR(1)模型和图3的ARMA(1,1)模型的比较, 选择ARMA(1,1)模型.

4. 模型的假设检验

在估计出的时间序列模型以后, 应该检验模型的确认是否正确. 检验通常是对残差进行的, 即残差的随机性检验. 若残差具有随机性, 意味着模型可以用于预测, 若残差不具有随机性, 说明所建的模型还需进一步的改进. 对ARMA(1,1)模型的残差序列进行检验如图4.

在图4的残差序列自相关—偏自相关分析图中, 自相关系数都落入了显著性水平为α=0.05的置性带内, 表示与0无显著差异,已经为白噪声序列, 说明拟合的模型已经充分提取了原序列的相关信息.

5. 模型的预测

经过对模型的类别的识别、定阶、参数估计和模型检验,获得较满意的时间序列模型后,可以用下面的模型(1)进行预测.

ARMA(1,1)模型参数估计与相关检验结果为:

图3 ARMA(1, 1)模型参数估计与相关检验结果

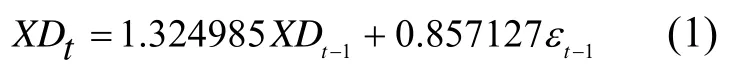
本文用ARMA(1,1)模型即模型(1)对2008年至2012年的湖南中小企业信用担保需求进行预测, 得到结果如表1.

表1中我们可以发现, 湖南中小企业信用担保持续增长, 从2008年的63.954亿元增加到2012年的197.1112亿元, 从下面的趋势图5预测的结果来看, 随着湖南社会信用体系的不断完善和资信评估业的不断发展、中小企业信用等级的提升以及担保组织的形式的多样化, 湖南信用担保业务作为一种中介服务活动将渗透到社会生活的各个角落, 湖南中小企业信用担保产业的发展方兴未艾. 因此我们同样可以合理预计: 经过十多年的探索和发展, 湖南信用服务产业的发展水平不断提高, 进入了发展期, 成为国民经济中一个新兴的服务行业; 随着湖南人均GDP的增加、市场开放度的提高、城市化水平的提升以及人们的科技文化水平的提高,湖南信用服务朝阳产业的发展前途光明.

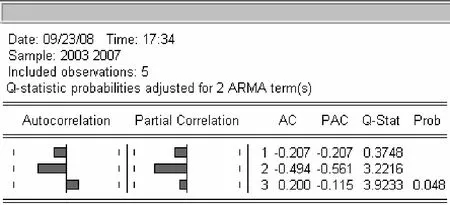
图4 ARMA(1, 1)模型的残差序列自相关—偏自相关分析图

表1 湖南2008～2012年中小企业信用担保预测结果 单位: 万元

图5 湖南中小企业信用担保预测趋势图

[1] 黎振强, 罗能生. 基于主成分分析的湖南信用服务产业发展水平综合评价[J].湖南理工学院学报(自然科学版), 2009, 22(1)

[2] 易丹辉. 数据分析与EViews应用[M]. 北京: 中国统计出版社, 2002

Forecasting the Development of Hunan Credit Services Industry Based on ARMA Model

LI Zhen-qiang
(Department of Economy and Management, Hunan Institute of Science and Technology, Yueyang 414006, China)

O213

A

1672-5298(2010)01-0028-03

2009-12-07

黎振强(1972- ), 男, 湖南岳阳人, 湖南理工学院经济与管理学院工程师. 主要研究方向: 国际贸易与制度创新