关于L-几何凸函数的不等式初探

吴光耀

(衢州高级中学, 浙江 衢州 324006)

关于L-几何凸函数的不等式初探

吴光耀

(衢州高级中学, 浙江 衢州 324006)

定义了一类新的几何凸函数—L-几何凸函数, 并用反向数字归纳法建立了这类几何凸函数的基本不等式,从而统一推行了一系列已知不等式, 包括一些著名不等式.

几何凸函数; L几何凸函数; 不等式; 高维推广.

Abstract:One type of convex function is defined in a new way as L geometric convex function. Moreover, a series of inequalities for this one type of geometric convex function are established, which is generalization of famous inequalities for general geometric convex functions.

Key words:geometric convex function;Lgeometric convex function; inequality; higher dimensional generalization.

众所周知, 凸函数是一个重要的数学概念, 在不等式研究中, 凸函数所发挥的作用是无可替代的[1,2],类比凸函数的概念, 文[3]中提出了如下几何凸函数的概念:

则说f (x)在D上是几何凸函数, 如果(1)中不等号反向, 则说f (x)在D上是几何凹函数．并建立了几何凸函数的一系列不等式, 文[4]作了更广泛的研究, 文[5]提出了l-几何凸函数的概念, 从中可以看出几何凸函数在不等式研究中具有重要的作用. 本文提出更一般的L-几何凸函数概念.

1 L几何凸函数的定义

为方便计, 引入下列记号: M = M1×M2×…×Mm( Mi为 [ai, bi], 或(ai, bi), 或无穷区间, i = 1, 2, …, m, m≥1). 若Mi== [0,+∞), i = 1, 2, …, m, 则M记作.

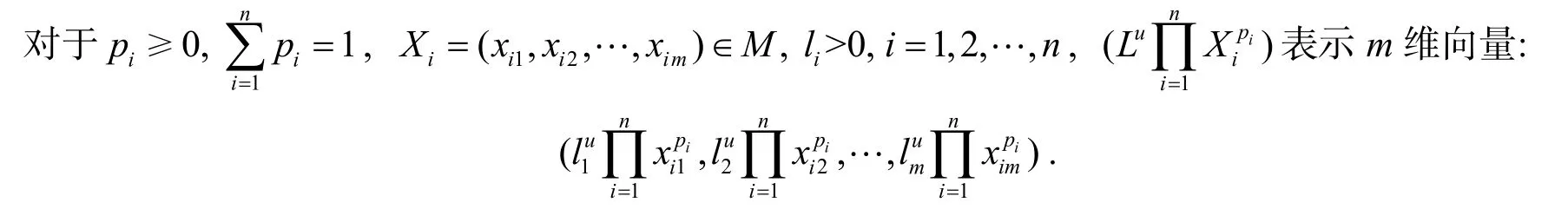
定义设f( X)是定义在D(⊆)上的连续函数, 若对任意的X1,X2∈M(⊆D), λ∈[0,1]和常向量L ,都有∈D , 且

则称f( x)是M上的L -几何凸函数; 如果(2)中的不等式反向, 则称f( x)是M上的L-几何凹函数.

2 关于L-几何凸函数的不等式

等式成立当且仅当X1＝X2= …＝Xn.

证明在定理2中令f( X)=lng( X), 即可得证.

注乘积型函数不等式中g( X)为正值函数的条件不可少, 否则结论不一定成立．这是因为 g( X)＜0时, －g( X)＞0, 用－g( X)替换推论2中的g( X), (12)式不变,当n为奇数时(13)式不等号反向．

定理3(算术型函数不等式) 设正值函数f (X)的定义域为, λ∈[0,1], 若对任意的X1、X2∈,都有

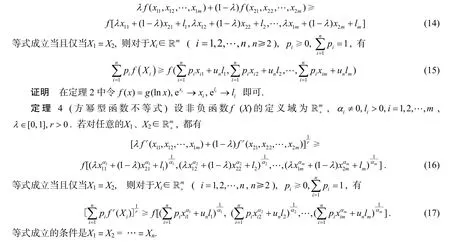
证明在定理3中, 令ϕ(x)=xαi, i=1,2,…,m , fr→f即可.

定理4的结果是多姿多彩的, 如取m = r = 1, l1 = 0, 则

①当α1=1时, 可得丹麦数学家Jensen (1859－1925)于1905年证明的著名的Jensen不等式;

② 当α1=-1时, 可得调和型函数不等式;

③ 当α1=k,( k∈N,k≥1)时, 可得乘方型函数不等式;

[1] Hardy G H, Littlewood J E. Polya G..不等式[M]. 越民义, 译. 北京: 科学出版社, 1965: 76～85

[2] Mitrinovic D. S, Vasic P. M. 分析不等式[M]. 赵汉宾, 译. 南宁: 广西人民出版社, 1986: 13～27

[3] 李世杰. 几何凸函数的若干性质[J]. 数学通讯, 2003(5): 37～40

[4] 吴善和. 几何凸函数与琴生型不等式[J]. 数学的实践与认识, 2004(2): 155～163

[5] 李世杰. 对函数几何凸性若干问题的理论研究[J]. 浙江万里学院学报. 2005 (2): 76～82

[6] 匡继昌. 常用不等式[M]. 第三版. 济南: 山东科学技术出版社, 2004

A Preliminary Study of L geometric Convex Function

WU Guang-yao
(Quzhou Senior High School, Quzhou 324006, China)

O178

A

1672-5298(2010)01-0013-04

2009-09-26

吴光耀(1960- ), 男, 浙江东阳人, 浙江衢州高级中学高级教师. 主要研究方向: 解析不等式