医院床位安排排队系统研究

程望斌, 周海燕

(1.湖南理工学院 信息与通信工程学院, 湖南 岳阳 414006; 2.岳阳职业技术学院 临床医学系, 湖南 岳阳 414000)

医院床位安排排队系统研究

程望斌1, 周海燕2

(1.湖南理工学院 信息与通信工程学院, 湖南 岳阳 414006; 2.岳阳职业技术学院 临床医学系, 湖南 岳阳 414000)

应用排队论理论, 对医院病床排队系统进行分析, 研究合理利用医院床位的组织方法. 设计相关排队算法, 提出了自适应排队模型, 分析在一定病床资源条件下, 通过对床位进行合理安排, 可提高病床的有效利用率和公平度, 并以一个实例进行了验证.

排队论; 病床安排; 队列长度; 病床利用率

Abstract:Queuing theory was used to make research on the queuing system of hospital beds, exploring how to arrange hospital beds and make best use of medical resources. Some queuing algorithm and self-adapting queuing model were proposed. The bed utilization and equitable degree, under certain bed conditions, were effectively improved with reasonable bed arrangements , and the method is validated by a case study.

Key words:queuing theory; bed arrangement; queue lengths; bed utilization

引言

医院就医排队是大家都非常熟悉的现象. 患者到门诊就诊、到收费处划价、到药房取药、到注射室打针、等待住院进行手术治疗等等, 往往需要排队等待. 病人到达时间和服务时间是随机的, 常会引起拥塞和病人长时间等待的现象, 从而降低了病人的满意度. 医院床位管理水平的高低, 是衡量和评价医院总体管理水平的重要内容之一. 通常情况下, 医院的病床资源与手术条件及相关服务是对应的, 在考虑病床安排时可不考虑手术条件的限制, 因此也不能单纯通过增加病床来达到减小等待住院病人队长的目的. 合理分析床位利用情况, 可以发现医院床位安排的不足和缺陷; 合理安排病床, 对于医院提高经济效益[1]、改善病房管理、挖掘内部潜力、增强服务能力具有重要意义.

为分析问题的方便, 以医院眼科病床安排为例进行研究.

1 病床安排系统模型

医院眼科手术主要分四大类: 白内障、视网膜疾病、青光眼和外伤. 其中, 白内障分为单眼和双眼, 若为双眼, 每次手术只能做一只, 两次手术时间间隔至少为1天, 白内障眼疾特点是住院治疗时间较短; 视网膜疾病和青光眼病理基本相同, 其共同特点是住院治疗时间较长; 外伤为急诊, 需优先安排入院和手术治疗. 这四类主要眼科疾病都需要进行住院治疗. 因此, 医院床位安排是否到位成为病人能否及早接受手术治疗的关键.

1.1 模型概述

以医院眼科住院系统为研究对象, 它有如下特征:

(1) 输入过程: 眼科患者的到达是相互独立的, 相继到达的时间间隔是随机的; 一定时间到达的概率分布服从泊松(Poisson)分布[2].

(2) 排队规则: 住院部对全体非急症病人采用FCFS(First come, First serve: 先到先服务)规则安排入院,且为等待制.

(3)服务时间: 各类眼疾患者住院时间是相互独立的, 且服从负指数分布.

(4)服务窗口: 多服务等待制排队问题, 眼科医院所有病床对应的是多个服务台, 这些病床并联排列且各病床独立提供服务.

1.2 模型假设与建立

假设眼科患者平均到达率为λ, 眼科医院有m个病床, 单个病床的平均服务率(表示单位时间内被服务完的患者数)为μ, 则整个医院病床的平均服务率为mμ; 系统的服务强度ρ=/m1 λμ＜时才不会排成无限长的队列; Pn(m)为m个病床任意时刻系统中有n个患者的概率; 当λ和mμ的生灭过程达到稳定时, 有

当系统达到平衡状态时, 每个患者在系统中等待时间W的均值为[3]

排队逗留的人数为

1.3 排队系统的优化特点

作为一个优化设计的系统, 应使患者损失费用和医院服务成本之和达到最小. 因此, 优化系统具有以下特点:

(1) 队长(排队系统中的病人数): 队长越短, 说明等待的病人越少, 排队系统设计越科学.

(2) 逗留时间(等待病床的平均逗留时间): 逗留时间越短, 给患者带来的损失就越小.

(3) 忙期(病床提供服务的平均时间): 忙期越短, 表明病床利用率就越高.

(4) 病床的利用率[4]: 病床利用率越高, 则病床安排的人数越多, 反映医院的效益就越好.

(5) 稳定状态概率(系统的服务强度): 稳定状态概率ρ＞1时, 等待的队列会越来越长; 反之队列会越来越短, 优化系统必定满足ρ＜1.

1.4 排队算法设计

排队算法设计的原理[5]: 病人安排病床的先后顺序由病人到达的先后顺序、住院治疗时间的长短以及病人所属类型的优先级别等综合确定. 眼科手术的四大疾病中, 外伤作为急诊, 优先级摆在第一位, 这是不容置疑的; 白内障需分为单眼和双眼病人, 其中双眼病人需分两次做手术, 每次一只, 且要间隔一天,因此白内障单眼和双眼眼疾病人应区分对待; 视网膜疾病和青光眼病理差别不是很大, 其共同特点是住院治疗时间较长. 考虑到白内障病人比视网膜疾病、青光眼病人的住院治疗时间短, 因此需优先考虑白内障病人特别是白内障双眼病人; 同时, 也要考虑病人已经等待了的时间和各类病人所占比例. 综合上述因素, 得眼科病人就诊优先级计算公式是

式(1)中, fi由相应的影响因子和权重确定: α1ti表示病人住院的优先与等待时间有关. 其中ti为某病人当前已经等待病床(入院)的时间;α1为该病人等待时间的优先权重, 等待时间长的病人应该适当考虑;α2βi表示病人住院的优先与该类等待住院的病人占总病人数的比例βi有关. 对同一类型的病人, 若其在总病人数中所占比例较大, 则应该适当考虑(β1+β2+β3+β4+β5=1, βi(i =1,2,3,4,5)分别表示外伤、白内障(单眼)、白内障(双眼)、视网膜疾病及青光眼五类眼科病人);α2为对队列长度的权重. α3si表示病人住院的优先与病人类型优先级有关, si表示不同类型病人优先级(外伤＞白内障双眼＞白内障单眼＞视网膜疾病和青光眼), 对优先级高的病人, 在服务上给予优先照顾; α3为病人类型的权重.

1.5 权重的确定

公式(1)中权重的大小直接决定了病人在队列中的相对位置, 对病人的满意度产生重要影响, 权重值的不同会导致不同的结果.

(1) 绝对优先: 病人的优先级占绝对重要因素, 比如作为眼科急诊的外伤, 此时α1=0,α2=0, α3=1.

(2) 无优先: 不考虑其它因素, 只按照FCFS规则输出住院序列, 此时α1=1,α2=0,α3=0.

(3) 有限度优先: 既考虑优先级又考虑等待时间和队列比例关系, 需分三种情况进行相关设置;权重采用层次分析法(AHP)获得.

2 实例分析

某医院眼科门诊每天开放, 住院部共有病床79张. 该医院眼科手术主要分四大类: 白内障、视网膜疾病、青光眼和外伤. 白内障手术较简单, 而且没有急症, 该院是每周一、三做白内障手术, 此类病人的术前准备时间只需1、2天, 做两只眼的病人比做一只眼的要多一些, 大约占到60%(如果要做双眼是周一先做一只, 周三再做另一只); 外伤疾病通常属于急症, 病床有空时立即安排住院, 住院后第二天便会安排手术; 其他眼科疾病比较复杂, 有各种不同情况, 但大致住院以后2～3天内就可以接受手术, 主要是术后的观察时间较长(这类疾病手术时间可根据需要安排, 一般不安排在周一、周三; 由于急症数量较少, 这些眼科疾病可不考虑急症). 该医院眼科手术条件比较充分, 在考虑病床安排时可不考虑手术条件的限制, 但考虑到手术医生的安排问题, 通常情况下白内障手术与其他眼科手术(急症除外)不安排在同一天做.

2.1 排队系统改进前

当前该住院部对全体非急症病人是按照FCFS规则安排住院, 但等待住院病人队列却越来越长, 医院方面希望能通过合理模型来帮助解决该住院部的病床合理安排问题, 以提高对医院资源的有效利用. 该医院2008年7月13日至2008年9月11日这段时间里各类病人的相关信息如表1所示.

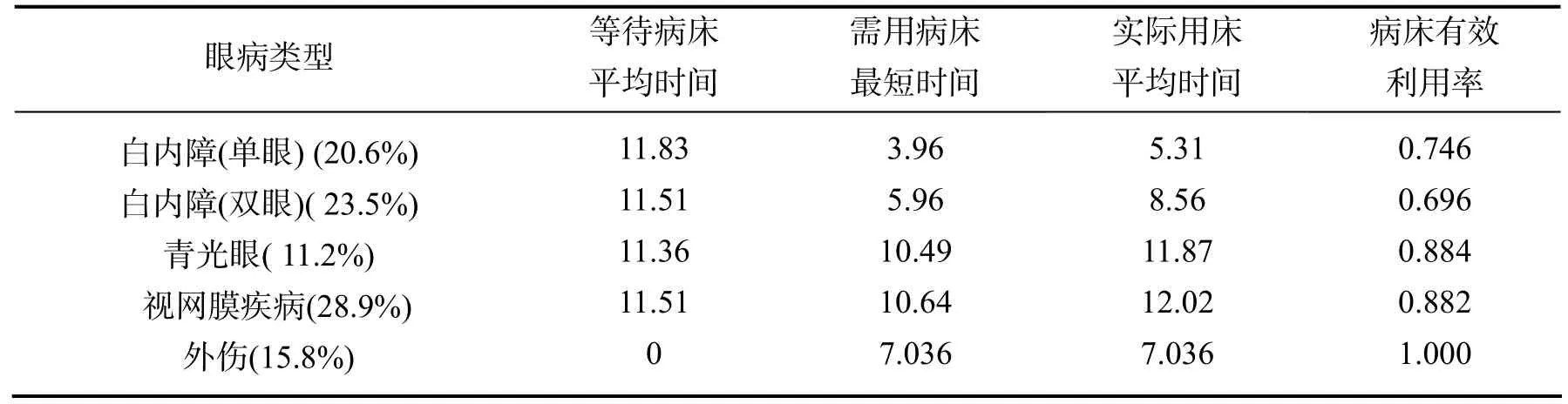
表1 各类眼科病人就医信息表

2.2 排队系统改进后

根据前面所建的排队模型, 我们编制了相关程序, 充分考虑了影响眼科病人住院优先级的各个因素,结合层次分析方法计算出各影响因子的相关权重, 最终计算出比较高效的病床安排. 利用新模型改进床位安排后的住院信息如表2所示.

表2 改进病床安排后的住院信息表

2.3 系统改进前后结果对比

改进病床安排方案后, 排队系统优势明显, 主要表现在: (1)队长变小, 排队系统中的人数越来越少,理论上队长可达到0; (2)逗留时间缩短, 降低了患者的危险和损失; (3)忙期减小, 病床使用更高效; (4)病床的利用率提高, 医院的经济效益得到了提升; (5)稳定状态概率ρ由大于1变成小于1, 即系统的服务强度和服务质量大大改善了.

2.4 系统模型的优化

从便于管理的角度提出建议, 在一般情形下, 医院病床安排可采取使各类病人占用病床的比例大致固定的方案, 为此需建立使得所有病人在系统内的平均逗留时间(含等待入院及住院时间)最短的病床比例分配模型, 即服务强度平衡模型. 该模型的基本思想是: 当各类眼科病人构成的排队系统的服务强度相同时, 总的系统服务效率达到最佳.

五类眼科病人排队系统的参数分别记为: 眼科患者平均到达率为λi, 单个病床的平均服务率为μi, 病床数为mi, i = 1, 2, 3, 4, 5. 则有

其中λi和μi(i=1,2,3,4,5)可以由统计数据得到. 按上述比例得到的各类病人床位比例即为最佳比例. 实际操作时, 急诊病人床位数可以根据需要作变动.

3 结束语

本文提出了一种自适应排队模型, 设计了排队算法, 并通过实例验证了该方法的有效性和可行性.

在有限的资源配置下, 利用上述排队模型理论和处理方法, 结合患者的服务记录获得相关数据, 对其作出定性和定量的评价. 通过对系统进行设计, 找出患者与医院之间的平衡点, 以提高医院现有病床资源的利用效率; 系统改进后, 不仅可提升医院的服务质量和服务水平, 改善医患关系, 而且, 还能降低患者的损失, 最大程度地获得经济效益和社会效益, 实现互利和双赢的目的.

[1] 吴小青. 医院病床利用与需求分析[J]. 中国医院统计, 1996, 3(2): 93

[2] 寿纪麟. 数学建模——方法与范例[M]. 西安: 西安交通大学出版社, 1993, 160～170

[3] 韩新焕, 朱萌纾, 吴 静. 医院管理系统中排队模型的优化决策分析[J]. 数理医药学杂志, 2008, 21(1): 17～18

[4] 王若瑾, 张慧芳. 应用“归一分析法”分析床位工作效率[J]. 医学信息学, 2008, 21(3): 25～26

[5] 张国通, 杜 刚, 江志斌, 等. 一种动态自适应医院门诊排队模型[J]. 上海交通大学学报, 2007, 41(1): 1546～1550

Research on the Queuing System of Hospital Beds

CHENG Wang-bin1, ZHOU Hai-yan2
(1. College of Information and Communication Engineering, Hunan Institute of science and Technology, Yueyang 414006, China; 2. Department of Clinical Medicine, Yueyang Vocational Technical College, Yueyang 414000, China)

O226

A

1672-5298(2010)01-0024-04

2009-12-16

程望斌(1979-), 男, 湖北崇阳人, 硕士, 湖南理工学院信息与通信工程学院讲师. 主要研究方向: 光电子学、数学建模