基于岩石长期稳定性的工程寿命预估研究

王来贵，李磊，刘学，王建国

(1.辽宁工程技术大学力学与工程学院，辽宁阜新 123000;2.煤炭科学研究总院沈阳研究院，辽宁沈阳 110015)

基于岩石长期稳定性的工程寿命预估研究

王来贵1，李磊1，刘学1，王建国2

(1.辽宁工程技术大学力学与工程学院，辽宁阜新 123000;2.煤炭科学研究总院沈阳研究院，辽宁沈阳 110015)

为了从岩石蠕变特性的角度对岩石工程的时效作用进行理论研究，通过对改进的西原蠕变模型进行理论分析，模拟微分方程数值曲线，从而得出与时间相关的蠕变加速度失稳判据;结合蠕变模型第三阶段的非线性特性，采用趋近系数对蠕变稳定阶段进行预测，对于非衰减蠕变破坏，通过破坏倾斜角进行预估。揭示了岩石第三阶段蠕变失稳的机理和规律，为预测岩石工程的失稳破坏及其寿命预估提供新的理论依据。

时效作用;蠕变模型;失稳判据;趋近系数;破坏倾斜角;工程寿命

0 引言

长期稳定性分析一直是岩石工程中重要的研究内容，而岩石流变力学特性与岩土工程长期稳定性紧密相关。工程实践与研究表明，岩体的失稳破坏与时间密切相关。对岩石流变力学特性的研究，国外学者做了很多有意义的探索。Griggs［1］提出砂岩、泥板岩和粉砂岩等类岩石受载达到破坏载荷的12.5%～80%时，就发生蠕变的观点。S.h.lz［2］认为脆性岩石蠕变现象是由于时间效应的岩石微破裂过程。A. Dragon［3］和D.M.Cruden［4］建立了时间效应微破裂数学模型。S.Okubo［5］通过实验获得岩石的三个阶段蠕变资料来预测岩体工程的破坏时间。

国内很多学者对岩石流变特性进行了比较成熟的研究。陈宗基［6］建立了岩石流变的扩容方程，并从岩石类材料结构特征出发，讨论了岩石微观结构的运动。刘雄［7］进一步探讨了结晶岩石内部缺陷扩散的蠕变机制。王子潮［8］结合蠕变不同阶段的试验观察与分析，对相应蠕变阶段微观蠕变机制的变化进行了具体描述。孙钧［9］、曹树刚［10］等建立了不同的蠕变模型，并阐述了确定模型蠕变参数的方法。王来贵［11］等提出了岩石蠕变失稳的概念，并在建立模型的基础上进行了初步应用。

目前对于如何评价岩石结构的收敛变形及稳定性等时效作用问题，大多局限于定性规律的把握，而对于流变力学特性定量程度的研究成果并不是很多。在岩石工程中，岩石蠕变特性有着重要的意义，尤其是蠕变第三阶段失稳特性，与岩石工程的长期稳定和使用寿命密切相关，且有待深入研究。

本文依据岩石流变力学理论，探讨外载荷恒定作用下岩石第三阶段蠕变导致失稳过程中岩体内随时间增长而发展的应力、应变及其作用的时间历程，得出蠕变加速度失稳判据并采用趋近系数对工程稳定性阶段进行寿命预估。成功地应用于露天高大边坡变形演化规律研究。

1 基于蠕变加速度的蠕变失稳判据

1.1 改进的西原模型蠕变过程分析

图1就σ0＞σf情形，结合改进的西原模型，对应力水平为0.47MPa、0.54MPa和0.64MPa三种情况进行了对比分析。参数取［12、13］:

由表达式可得，前期指数占据主要地位，曲线呈凹型，随着t的增大，指数迅速减小，二次多项式逐渐增大，曲线过渡到开口向上的抛物线型。

图1 改进的西原模型的特征曲线Fig.1 Creep chracteristic curves of K-B model

分析表达式可得，前期指数占据主要地位，但由于系数为负数，曲线呈凸型，随着t的增大，指数迅速减小，一次多项式逐渐增大，曲线逐步过渡到斜直线，直线贯穿于第二、第三两个蠕变阶段，并在第二阶段与水平轴交于一点，所对应的时间暂定为临界时间，这里用tc表示。

对比图1的9条曲线可得:

(1)随着时间增加，应变加速度由负值变为正值;同时随着应力水平提高，曲线的数值也相应扩大。

(2)应变加速度为零的时刻分别为t1、t2、t3，且t1＜t2＜t3，说明了随着应力的减小，应变加速度的临界时刻随之延后。

(3)在应变速率－时间曲线上，t1、t2、t3时刻，分别对应着各自曲线的最小值，即应变速率以此为时间分界点，之前递减，之后递增。

(4)在应变－时间曲线上，t1、t2、t3时刻，分别对应着各自蠕变稳定阶段的拐点值，但从此刻起，蠕变就进入了加速发展阶段，如果应力水平不再降低，则必然导致破坏，因此，把t时刻作为岩石失稳的下限具有一定的意义。

1.2 失稳判据

(1)当t＜tc，即(t)＜0，蠕变由第一阶段逐渐过渡到第二阶段，系统处于稳定状态。

(2)当t=tc，即(t)=0，蠕变处在第二阶段，系统处于临界状态。

(3)当t＞tc，即(t)＞0，蠕变由第二阶段逐渐过渡到第三阶段，最终导致系统失稳破坏。

1.3 应力－临界时间关系曲线

令该模型的蠕变加速度¨ε=0，化简后得:式中t就代表临界时间，如果把t看做自变量，σ0看做因变量，则:

反映了初始应力与临界时间的反函数关系，参数仍取:

此时关系曲线如图2。从图2中不难发现，当纵坐标对应的初始应力σ0→σf时，即应力由0.59→0.44MPa时，横坐标所对应的临界时间逐渐增大，并且初始应力越接近长期强度(越低)，临界时间增长就越快，当初始应力等于长期强度时，临界时间趋于无穷;相反，当应力高到一定程度时，应力的增加，只会引起临界时间略微减小。

2 岩石工程稳定性寿命预估

2.1 衰减蠕变稳定阶段起始时刻预测

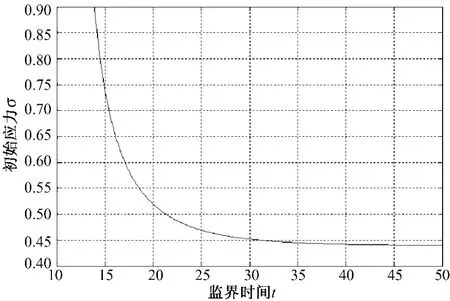
图2 应力－临界时间曲线Fig.2 Stress-critical time curves

岩石蠕变分为衰减蠕变和非衰减蠕变两种过程，前者最终趋于稳定，后者最终导致破坏。在衰减蠕变过程中，位移最终保持稳定，衰减蠕变稳定阶段的起始时间可由位移的趋近程度来表示:

式中K暂称为趋近系数，K越趋近于1则说明蠕变越趋于稳定。如果令u(t)为稳定阶段的起始阶段，则可通过位移的反函数求得:

如1993年，墓坪滑坡体的滑动在经过约5个月的滑动后逐渐停止，其位移表达式为:

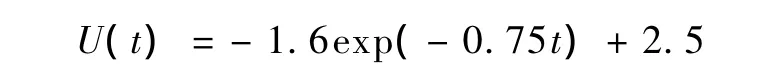
其位移极限U(∞)=2.5m，墓坪滑坡体的滑动位移的趋近系数:

墓坪滑坡体的位移－时间曲线和趋近系数－时

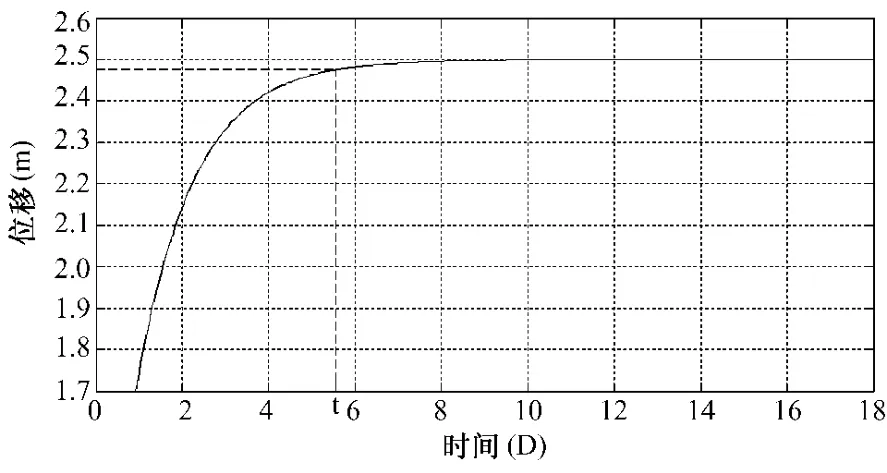
图3 位移－时间曲线Fig.3 Displacement-time curve

间曲线如图3:从图4可看出随着时间的增长，趋近系数逐渐接近1，当趋近系数取0.99时，对应的时间大约在5.5d，在位移－时间曲线上可以发现位移开始趋于稳定，可见趋近系数一般取0.99～1。

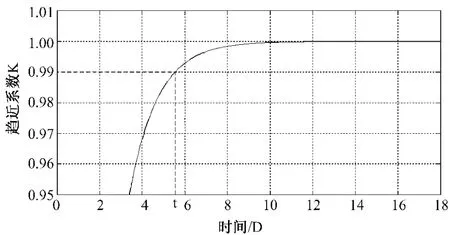
图4 趋近系数－时间曲线Fig.4 Reaching coefficient-time curve

2.2 非衰减蠕变破坏时刻预测假设

岩土蠕变曲线的3个阶段被视为滑坡预测预报的基本标准［14］。王家鼎［15］等人在对岩体滑坡时间预测的研究中，认为当位移与时间关系曲线上某点的切线与横坐标(时间)的夹角成90°时，即tanα→∞，时，滑坡发生，该点所对应的时间为破坏时间;之后，对大量黄土滑坡的统计结果分析表明，变形曲线的斜率在89°～89.5°时所对应的时间段为滑坡发生的危险段更接近实际(图5)，F点即为滑坡发生的破坏点。

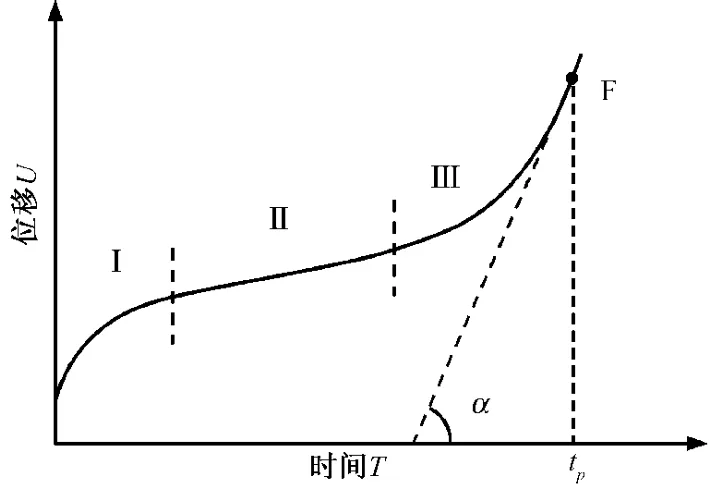
图5 滑坡位移曲线Fig.5 Landslide displacement curve

由此启发，考虑到边坡容易出现较大位移，不同于其他性质的岩石工程，分别假设岩石的蠕变曲线和蠕变速率曲线的斜率夹角α达到某一程度时，即发生破坏，据斜率夹角α可得出与破坏时刻的关系:

(1)对于容易产生较大位移的岩石工程(如边坡)，可假设:

式中:tp——岩石的破坏时间;

F－1(t)——F(t)的反函数。

(2)而对于严格限制变形的岩石工程，如地下洞室工程等，可以假设岩石蠕变破坏时间与位移速率的斜率有关，岩石的破坏时间可表示为:

3 结论

(1)改进的西原模型可以较完善地反映岩石蠕变的三个阶段，尤其是非线性加速蠕变阶段。

(2)与改进的西原模型蠕变加速度曲线相结合，考虑蠕变加速度符号变化情况，据临界时间tc建立蠕变加速度与稳定性的对应过程，得出失稳判据。

(3)结合改进的西原模型，预估蠕变过程中的相关时间。在衰减蠕变过程中，稳定阶段的起始时间可由位移的趋近系数来求得。在非衰减蠕变过程中，蠕变破坏时间可由破坏倾斜角来求得。

(4)本研究成功地应用于露天高大边坡变形演化规律研究。

［1］Griggs D.Creep of rocks［J］.Geol.1939:47.

［2］Scholz C H.Experimental study of the fracturing process in brittle rock［J］.Geophys Res，1968，73:1447－1454.

［3］Dragon A，Mroz Z.A continue model for plastic－brittle behavior of rock and concrete［J］.Engng.Sci，1976，17: (17):121－137.

［4］Cruden D M.A theory of brittle creep in rock under uniaxial compression［J］.Geophys Res，1970，75(17): 3431－3442.

［5］Okubo S，Fukui K，Nishimatsu Y.Control performance of servo－controlledtestingmachinesincompressionand creep tests［J］.International Journal of Rock Mechanics and Mining Sciences＆Geomechanics Abstracts，1993，30 (3):247－255.

［6］陈宗基，康文法，黄杰藩.岩石的封闭应力、蠕变和扩容及本构方程［J］岩石力学与工程学报，1991:(4): 299－312.

［7］刘雄，吴德伦.岩石流变学概论［M］.北京:地质出版社，1994.

［8］王子潮，王绳祖.地壳岩石半脆性非均匀蠕变本构模型［J］岩石力学与工程学报，1990(2):164－173.

［9］孙钧，赵明阶.岩土材料流变及其工程应用［M］.北京:中国建筑工业出版社，1999.

［10］曹树刚，边金，李鹏.岩石蠕变本构关系及改进的西原正夫模型［J］.岩石力学与工程学报，2001，21(5): 632－634.

［11］王来贵，何峰，刘向峰，等.岩石试件非线性蠕变模型及其稳定性分析［J］.岩石力学与工程学报，2004，23 (10):1640－1642.

［12］邓荣贵，周德培，张倬元，等.一种新的岩石流变模型［J］.岩石力学与工程学报，2001，20(6):780－784.

［13］何峰，王来贵，于永江，等.岩石试件非线性蠕变模型及其参数确定［J］.辽宁工程技术大学学报，2005，24 (2):181－183.

［14］王来贵，刘向峰，王玉富.岩石力学系统的基本问题［J］.辽宁工程技术大学学报，2001，20(4):439－401.

［15］王家鼎.高速黄土滑坡的一种机理——饱和黄土蠕动液化［J］地质论评，1992，38(6):532－539.

Abstract:In order to do theoretical study on time－effect combining of an engincered rock from the point of view of creep properties of rock，instability criterion of creep acceleration interrelated with time was proposed based on theoretical analysis of improved creep K－B model and simulation of differential equations of numerical curve.For forecasting the stable stage of creep using reaching coefficient in combination with nonlinear characteristics of the third stage of K－B model，the concept of failure of tilt angle was put forward for non attenuation creep failure.The paper revealed the mechanisms and rules of creep instability on the third stage of crock，and provided new theoretical basis for forecasting the instable failure and life prediction of rock engineering.

Key words:time－effect;creep model;instability criterion;reaching coefficient;failure of tilt angle;life of engineering

Life expectation of an rock engineered slope based on the long-term stability

WANG Lai－gui1，LI Lei1，LIU Xue1，WANG Jian－guo2
(1.School of Mechanics and Engineering，Liaoning Technical University，Fuxin123000，China; 2.Shenyang Branch of China Coal Research Institute，Shenyang110015，China)

1003－8035(2010)03－0097－04

P642.3;TU457

A

2010－05－07;

2010－06－01

地质灾害防治与地质环境保护国家重点实验室开放基金资助项目(DZJK－0809);国家自然科学基金重点资助项目(10972096;50774046)。

王来贵(1962—)，男，山西闻喜人，博士，教授，主要从事岩石力学系统稳定性理论、环境岩石学方面研究。

E－mail:wanglg128@vip.sina.com