基于小波变换的纸浆结构统计模型的研究

周 强 南 楠

(陕西科技大学电气与信息工程学院,陕西西安,710021)

基于小波变换的纸浆结构统计模型的研究

周 强 南 楠

(陕西科技大学电气与信息工程学院,陕西西安,710021)

在研究纸浆纤维形态、结构的基础上,建立纸浆的数学模型,并根据纸浆纤维分布与纸浆浓度的关系提出了在线确定纸浆数学模型参数的方法。具体步骤是:对纸浆浓度信号进行小波变换,根据小波谱的周期和峰值分别计算纸浆纤维团的半径和纤维团的中心距离,进而确定纸浆数学模型的参数。实验表明,该方法能建立准确的纸浆数学模型。

纸浆纤维分布;纸浆数学模型;纤维团半径;纤维团中心距离;小波变换

在造纸生产中,由于纸浆的纤维形态、结构与成品纸张的匀度、耐破度等很多指标密切相关。因此,对纸浆结构模型,特别是结构数学模型的研究具有重要意义[1]。目前,数字图像技术(D IT)[2]、超声波脉冲多普勒法(PUD)[3]、核磁共振(NMR)法[4]等多种方法被用于纸浆模型的研究。不过这些方法或是因价格昂贵及使用条件限制不适合在生产环境下使用,或是无法实现对纸浆纤维的形态与结构(即纸浆纤维在纸浆中的分布规律)进行在线测量。本研究在建立纸浆纤维物理模型的前提下,提出对纸浆浓度信号进行连续小波变换,在线确定纸浆的统计数学模型。实验结果表明,该方法建立的数学模型能够准确、实时地反映不同状态下纸浆纤维的分布规律。

1 纸浆纤维的结构特点及其模型

1.1 纸浆纤维的结构特点

纸浆是水中悬浮着纤维和气体的三相流体[5]。根据流变学理论,纸浆中的纤维以游离和团聚两种形态存在[6]。趋于团聚形成所谓絮状纤维团是纸浆纤维的一个主要特点,纸浆中的大多数纤维在绝大多数浓度(除了浓度极低)下都是以团聚形态存在;剩余的纤维以游离态悬浮在水中。随着纸浆状态的变化,两种形态的纤维之间会发生相互转化。在纸浆浓度提高或纸浆流速降低时,团聚形态的纤维增加,纤维团体积增大,游离态的纤维减少;纸浆流速提高时,由于浆流的湍流作用加强,一些纤维团边缘的纤维克服团聚作用,成为游离态的纤维,纤维团体积减小[7]。此外,添加物的更换及添加量的改变也会引起纸浆纤维形态的变化[8]。

1.2 纸浆的物理模型

在目前的研究中,通常采用纤维网状和纤维团(块)两种结构来近似纸浆纤维的形态[2]。同时,采用这两种结构建立纸浆的物理模型。在模型中,纸浆纤维依靠氢键的结合力以网状相互连接形成絮状纤维团,假设这些纤维团的形状近似为球形,并且自由地分散在纸浆中,那么其大小及分布位置都是随机的,且随着纸浆状态的变化而改变。

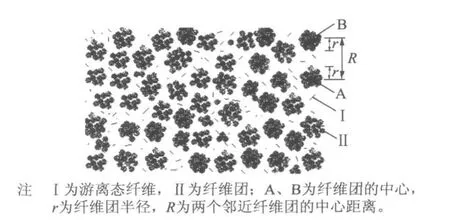
图1 纸浆纤维的物理模型

由图1可见,不同半径的纤维团和游离态的纤维随机地分布在纸浆中。在当前的工艺条件下,由于纸浆纤维多以纤维团形式存在,因此,纸浆纤维模型主要由纤维团构成,而游离态纤维被忽略。

1.3 纸浆纤维的数学模型

纸浆纤维的物理模型不仅接近纸浆纤维的真实结构,而且由此也容易建立纸浆纤维的数学模型。由于纤维团半径r、纤维团中心距离R可以较全面地反映纸浆纤维的形态和结构,据此可建立纸浆纤维的数学模型(见式(1)和式(2),虽然r和R均是随机变量,但都服从一定的分布规律):

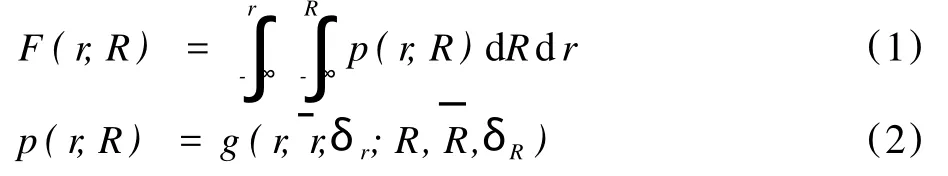
式(1)是一个二维分布函数,它反映出随机变量纤维团半径r和纤维团中心距离R围绕平均值和的分布情况。式(2)是r、R的分布密度函数,其中δr和δR分别为r和R的标准差。式(1)和式(2)表示了纤维团大小及其在纸浆中的位置,可定量描述纸浆纤维的实时形态和结构。

2 基于小波变换的纸浆纤维数学模型参数的在线确定

2.1 纸浆纤维分布与纸浆浓度的关系

造纸生产中纸浆浓度的测量方法以力学法为主,这是一种利用流体黏度和密度测量纸浆浓度的间接方法[9]。根据流体边界层理论,当黏性流体(纸浆)沿固体(浓度传感器的测量元件)表面流动时,在靠近固体表面的边界层内会形成很大的流速梯度。按黏性流体的内摩擦定律,一层厚度为dh的流体层的两表面若有dv的速度差,则该流体层和相邻的固体表面或其他流体层之间存在剪应力τ,在一定的面积A上,则体现为互相作用的集中剪应力F[10],因此,F反映了纸浆浓度c的大小(见式(3))。

对于由纸浆纤维、水和气泡组成的不均匀混合物来说,纸浆纤维团对应的dτ很大,水和气泡对应的dτ较小,从而造成了F的波动,进而引起纸浆浓度c的波动。值得说明的是,这种波动并非测量误差,而是纸浆浓度不均匀的真实反映,它实际上是纸浆纤维团在纸浆中随机分布的结果。在纤维团流经传感器处时,纸浆浓度测量值偏高;而在各个纤维团之间的水和气泡流过时,纸浆浓度测量值偏低,这个过程反映到纸浆浓度信号上,纸浆浓度信号会出现忽高忽低的起伏。因此,纸浆纤维在纸浆中的分布情况直接反映到纸浆浓度测量值的波动中(见图2)。

从图2可见,纸浆浓度的随机波动。纸浆纤维团的半径r以及纤维团中心距离R等有用信息都包含在纸浆浓度信号c(t)的波动之中,对纸浆浓度信号(t)采用小波变换等时-频分析手段能够计算出r和R,从而获得纸浆纤维的分布情况。

2.2 相邻纸浆纤维团中心距离的在线测量

纸浆浓度信号c(t)根据式(4)进行小波变换,并使用M exican Hat函数ha,b(t)作为母小波(见式(5)),式(4)中(t)是ha,b(t)的共轭。式(5)中平移因子b和尺度因子a分别代表时-频空间的时间轴和频率轴。

图3是纸浆浓度信号c(t)的小波谱,其中的明暗间隔是由纸浆浓度信号波动引起的。笔者发现,在同一尺度a上,即沿着横坐标方向,阴影部分(即峰值W Tmax(a,b))的间隔周期Ta可以反映相邻纸浆纤维团中心距离R,它们的对应关系由式(6)表示:

式(6)中,n为R的序号,k′为常数,v为纸浆流速。因此,由式(7)可计算出纸浆中某处两个相邻纤维团的中心距离R。由于纤维团分布的随机性,Rn是一个随机序列,R的平均值、标准差δ分别由式(8)和式(9)计算:

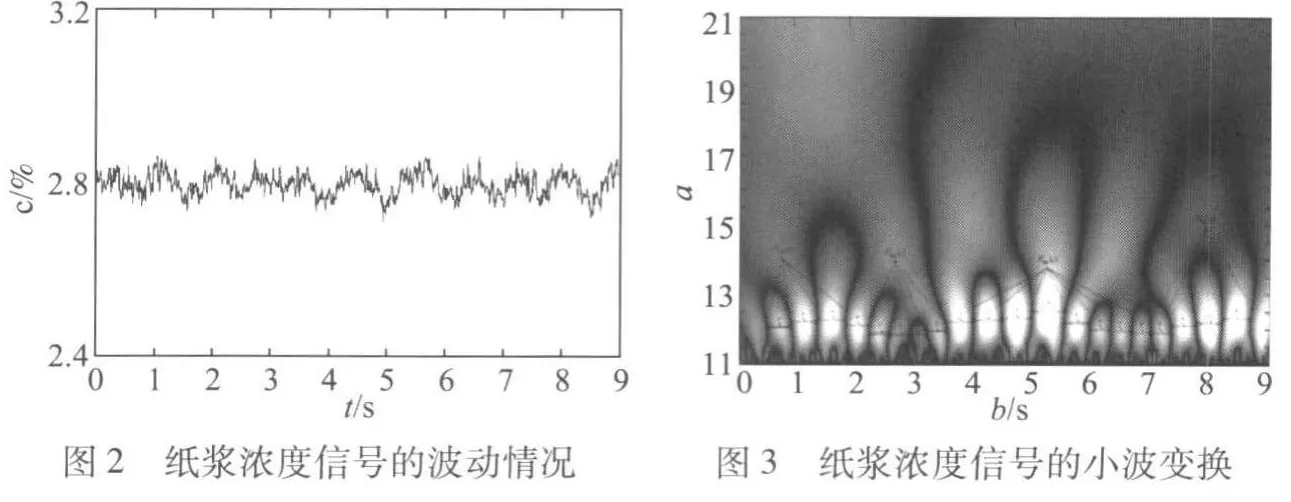
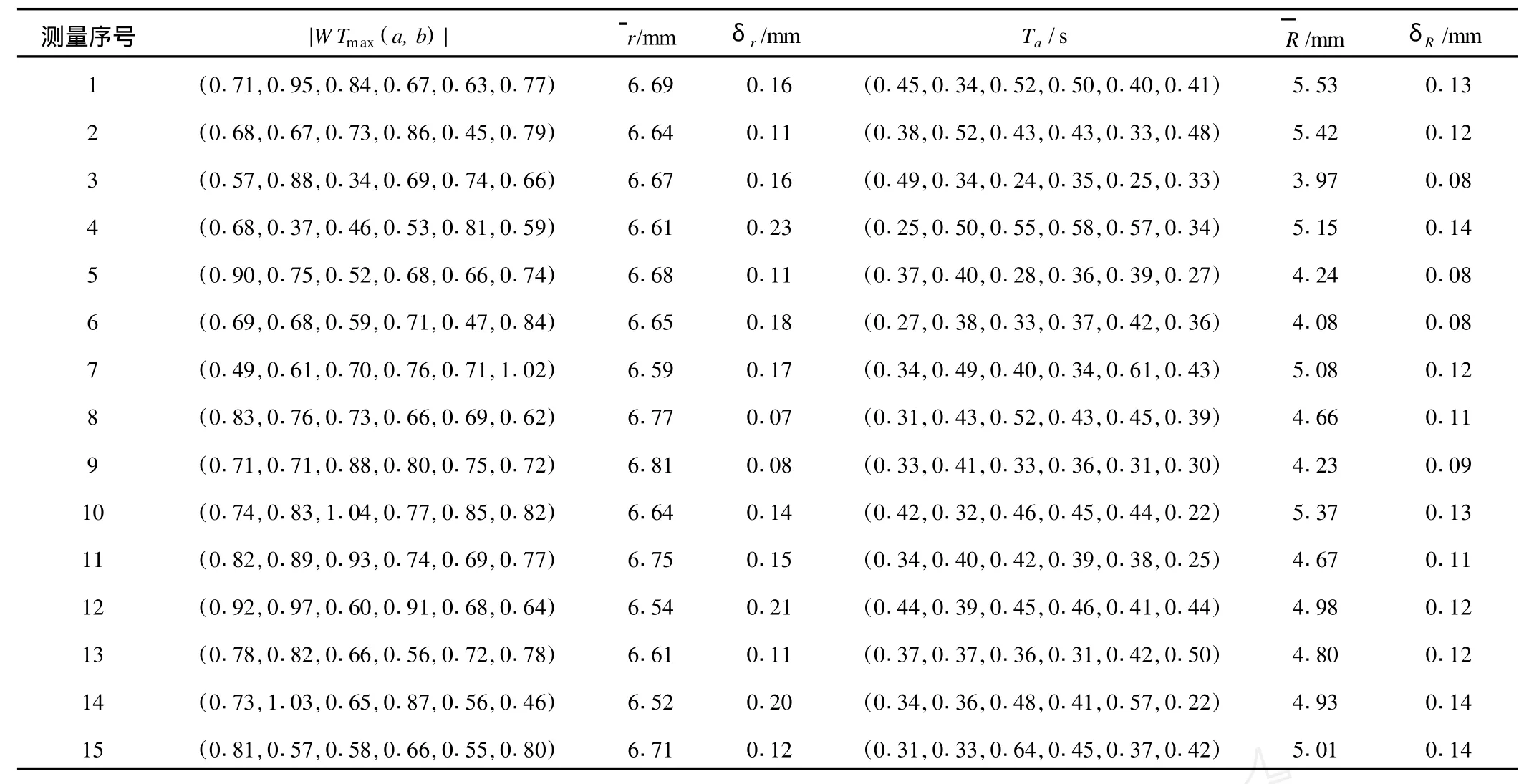
表1 纸浆纤维团中心距离的部分数据

式(8)和式(9)中的N是Rn的个数。

2.3 纸浆纤维团半径的在线测量

纸浆纤维团的半径也可以通过纸浆浓度信号的小波谱获得。笔者发现,每个小波谱的峰值W Tmax(a, b)实际上都对应着一个纤维团的半径rn,在一定的纸浆浓度和流速范围内,rn和W Tmax(a,b)近似有以下的线性关系:

由式(10)可以得到纸浆纤维团半径的近似值,其中k为经验常数。利用式(11)和式(12)可计算r的平均值和 标准差。

3 实验及结果分析

将以上介绍的方法应用于造纸生产线上,对流浆箱前一台旋转式浓度计的信号进行采样和记录,获得纸浆浓度信号c(t);为了保留其中的波动成分,不对c(t)进行软硬件滤波处理。利用式(4)对c(t)进行连续小波变换,获得小波谱W T(a,b);利用式(7)～式(12)得到R及统计参数δr、、δR。表1和表2为部分原始数据和实验结果。

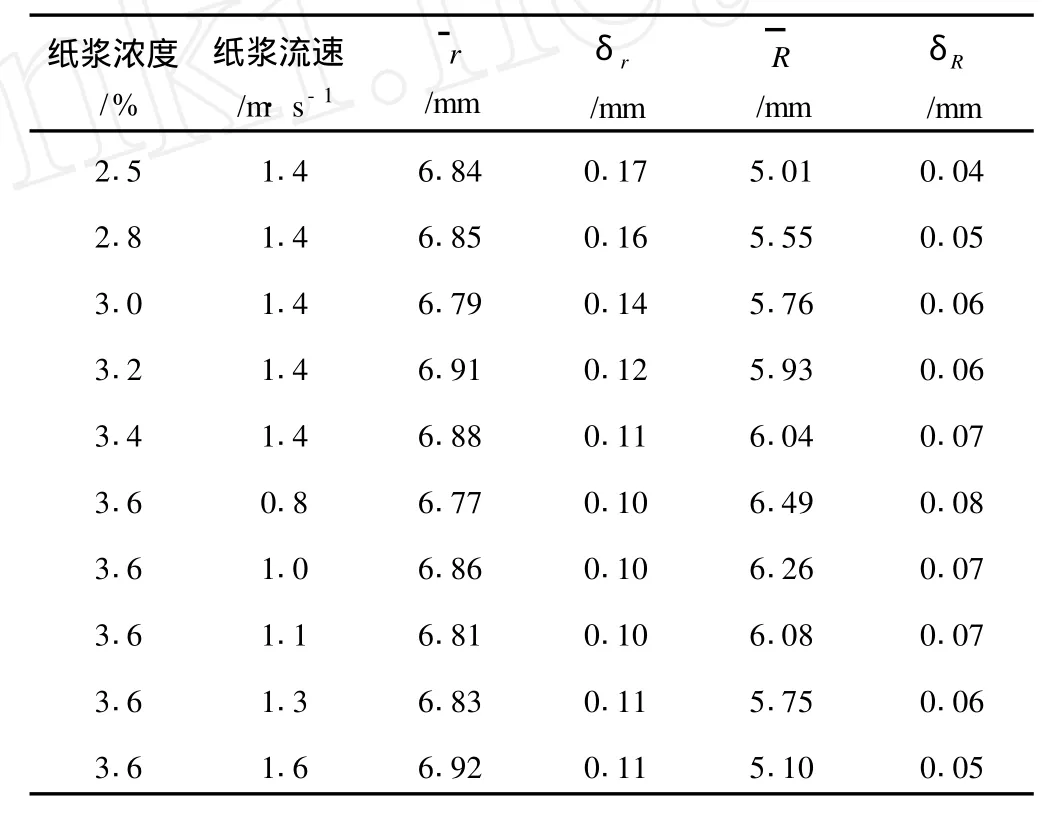
表2 纸浆浓度和流速对纸浆纤维分布的影响

(2)纸浆的流速和浓度均对纸浆纤维分布有显著影响。在纸浆浓度不变的情况下,随着纸浆流速的提高,纸浆纤维团半径r减小,而纤维团之间的平均距离基本不变,纸浆浓度标准差减小,纸浆浓度的波动幅度趋于平缓;在纸浆流速恒定的情况下,随着纸浆浓度增加,纸浆纤维团半径r及平均半径增 大,δR减小,而纤维团之间的平均距离保持恒定。

根据上述第一个结果,可以将纸浆纤维数学模型的概率密度公式(2)确定为:

式(13)反映出纸浆纤维团半径r和中心距离R呈现二维高斯分布。第一个结果还反映出在纸浆流速一定的情况下,纸浆浓度信号的平均频率基本恒定,这个结果对于研究和改善纸浆浓度传感器的性能、分离纸浆浓度中的信号与噪声、大幅度提高纸浆浓度的测量精度均有帮助;并且通过对纸浆浓度信号的时-频分析还可以获得纸浆的流速信息[11]。第二个结果反映出纸浆流速和浓度的波动都会改变纸浆纤维的分布规律,从而影响成纸质量。因此,获得高质量的成品纸张,纸浆纤维的分布将成为一个重要指标。

4 结 语

本文介绍了对纸浆浓度信号进行小波分析从而获得纸浆性质的方法。该方法能够在线获得纸浆纤维结构数学模型的参数,从而确定纸浆的统计概率模型,进而实现实时、定量地描述纸浆纤维的分布规律。不仅为进一步提高纸浆浓度的测量精度带来帮助,也为在线预测造纸生产线上成纸的一些主要物理性能提供依据。

[1] HouraniM.Fiber flocculation in pulp suspension:Part1:Theoretica model[J].Tappi J.,1988,71(3):115.

[2] Cui H,Grace J R.Flow of pulp fibre suspension and slurries:A re view[J].International Journal ofMultiphase Flow,2007,33(1):9.

[3] Xu H J,Aidun C K.Characteristics of fiber suspension flow in a rec tangular channel[J].Int.J.Multiphase Flow,2005,31(9):318.

[4] Arola D F,Powell R L,McCarthyM J,et al.NMR imaging of pulp suspension flowing through an abrupt pipe expansion[J].A IChE J., 1998,44(12):2597.

[5] Kerekes R,Schell C J.Characterization of Fibre Flocculation Re gimes by a Crowding Factor[J].Journal of Pulp and Paper Science, 1992,18(3):167.

[6] 陈克复,杨仁党,侯庆喜.纸浆与漂白剂的混合机理与纸浆流变学[J].中国造纸学报,2001,16(1):23.

[7] Duffy G G.Flow ofMedium Consistency ofWood Pulp Fibre Suspen sions[J].Appita,2003,48(2):51.

[8] Huber P,Roux J C,Mauret E,et al.Suspension Crowding for General Fibre-LengthDistribution:Application to Flocculation ofMix tures of Short and Long Papermaking Fibres[J].Journal of Pulp and Paper Science,2003,29(3):102.

[9] 陆国强,富乃成,郑志受,等.纸浆浓度在线测试方法的研究[J].计量学报,2001(1):74.

[10] 周 强,韩九强.提高力学法纸浆浓度测量精度的研究[J].中国造纸学报,2008,23(2):100.

[11] Zhou Q,Han J Q.Research of Time-frequency AnalysisMethod o Nonstationary Periodic Signal[C]//2008 IEEE International Confer ences on CIS&RAM.Chengdu,2008.

Abstract:On the basis of studying the behaviour of fiber suspensions,mathematical model of pulp suspension is established,and on-lin method to get parameters of the mathematicalmodel is put for ward according to the relationship between the pulp fiber distribution and th pulp consistency.The detailed calculating steps are proposed,firstly,the pulp consistency signal conductswavelet transform,then the radiu of fiber conglomerations and the central distances of adjacent fiber conglomerations are calculated based on the period and peak value of th wavelet,accordingly the parameters of pulp mathematicalmodel can be decided.The corresponding tests show that the precise mathematica model of pulp suspension can be obtained by the method.

Keywords:pulp fiber distribution;pulp suspension mathematical model;radius of conglomeration;central distance of conglomeration; wavelet transfor m

(责任编辑:关 颖)

StatisticalM odeling of Pulp Suspension Structure Based on Wavelet Transform

ZHOU Qiang＊NAN Nan

(School of Electronic and Infor m ation Engineering,Shaanxi University of Science and Technology,Xi'an,Shaanxi Province,710021)
(＊E-mail:zhouqtz@126.com)

TS749

A

1000-6842(2010)02-0067-04

2009-12-29(修改稿)

本项目得到国家科技支撑计划项目(2006BAF02A280)、陕西科技大学科研启动基金项目(BJ10-05)的资助。

周 强,男;博士,副教授;研究方向:智能信息处理及软测量。

E-mail:zhouqtz@126.com