滑坡频度-降雨量的分形关系

李长江，麻土华，李炜，郑爱平，朱兴盛

(1.浙江省国土资源厅信息中心，浙江杭州 310007;2.浙江省国土资源厅地质环境处，浙江杭州 310007; 3.浙江大学地球科学系，浙江杭州 310027)

滑坡频度-降雨量的分形关系

李长江1，麻土华1，李炜2，郑爱平3，朱兴盛1

(1.浙江省国土资源厅信息中心，浙江杭州 310007;2.浙江省国土资源厅地质环境处，浙江杭州 310007; 3.浙江大学地球科学系，浙江杭州 310027)

降雨－滑坡关系是对降雨引发的滑坡进行预报的一个重要基础。本文根据中国浙江省1990～2003年期间有明确日期和坐标记录的1414个滑坡数据和基本覆盖浙江全部陆地区域的1257个雨量站记录的日降雨量数据，研究了滑坡频度－降雨关系。研究结果表明，降雨引发滑坡的频度与降雨量之间遵循分形的幂指数关系，并且在两个尺度的降雨量范围内具有不同的标度指数。按照幂指数关系拟合的两条滑坡累计频度－降雨关系线交点(拐点)处的降雨量(Rin)指出了引发75%左右滑坡的累计降雨阀值的上边界(以THCR表示)。对1d、4d、6d和11d这4个累计降雨时段的研究表明，引发75%左右滑坡的累计降雨阀值分别为205mm(1d)、273mm(4d)、294 mm(6d)、315 mm(11d)。

滑坡频度;降雨阈值;幂指数分布;分形;浙江省

0 引言

滑坡(土体和岩体滑动、也包括泥石流和崩塌等)是山区经常发生的灾害。在各种自然因素引发的各类滑坡中，以降雨引发的滑坡，即降雨型滑坡［1］发生的频度最高，分布的地域最广，造成的灾害最严重，是滑坡预报研究的主要对象。目前一般认为，雨水渗入斜坡岩土体后导致其内部孔隙压力增大及有效应力减小是降雨型滑坡发生的主要机制。

Caine(1980)在全球范围收集了前人报导的73处浅层滑坡(shallow landslides)点附近的降雨记录，他把峰值降雨强度和历时标绘在双对数坐标图上得到了一个滑坡发生的降雨阀值［2］。此后，不少研究者在世界许多地方对这种方法做了进一步的研究［3－10］(如:Wieczorek，1987;Cannon，1988;Larsen和Simon，1993;Wilson和Wieczorek，1995;Glade等，2000;Wieczorek等，2000;Aleotti，2004;Guzzetti等，2007)，提出了各种区域或地方性滑坡发生的降雨阀值。然而，现有确定降雨阀值的各种统计方法一般都没有把降雨与引发的滑坡频度联系起来。

在许多国家和地区，航空照片解译是最主要和应用最广泛的滑坡填图方法。采用航空照片解译进行滑坡填图通常是在较大的滑坡事件之后，甚至是几年以后进行的，按发生年份记录的滑坡数据相当罕见［11］，以至难以确定有关滑坡发生的日期或时间。与滑坡数据相比，在一些建有雨量站的地方通常可以获得较完整的降雨记录。这种情况或许就导致了自Caine(1980)以来，对滑坡－降雨关系的研究几乎主要围绕降雨强度－历时关系进行。只有少数研究者关注到滑坡发生频度和降雨的关系，如Finlay等(1997)曾在香港根据1984～1993年期间的791个数据，使用一次、二次和三次曲线拟合分析了滑坡发生数和降雨的关系［12］。后来，Dai和Lee(2001)使用香港在1984～1997年期间的数据对滑坡和降雨的关系作了进一步分析［13］。

由于地理位置、地质和地形的原因，浙江是中国降雨型滑坡最频发的地区之一，每年都会因降雨引发大量浅层滑坡，对公众生命和经济造成严重危害。本文根据在1990～2003年期间发生的既有发生日期(时间)又有坐标记录的1414个滑坡和1257个雨量站在1990～2003年期间记录日降雨量数据，讨论滑坡频度与降雨分布的关系。

1 研究区和数据

浙江位于中国东南沿海(图1)，陆域面积10.18 ×104km2。浙江地形复杂，地势高低悬殊。标高在300m以上的丘陵和山地约占全省面积的70.6%。整个地势由西南向东北倾斜，呈阶梯状下降。浙西南部为地势高峻，大多为平均海拔800m以上的山区，最高海拔处1929m;中部以丘陵为主，大多为500m以下的低山丘陵，在丘陵山地之间分布一些盆地;东北部是低平的冲积平原，平均高程2～5m。

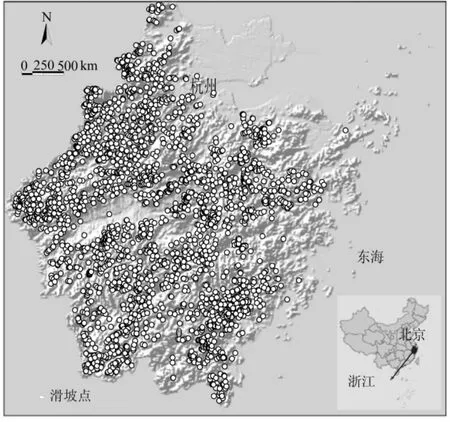
图1 浙江地势。图中白色圆点表示1990-2003年期间发生的有日期和坐标记录的1414个降雨引发的滑坡。Fig.1 Topographic map of Zhejiang Province showing the spatial distribution of rainfall-induced landslides. White dots are the locations of 1414 landslides having the recorded date of occurrence in the 1990-2003 period.Inset shows the location of Zhejiang in southeastern China.

如图2所示，地层的分布大致以北东向的江山─绍兴断裂为界，浙西北区除了少量火山岩层，花岗岩，以及分布在个别断(坳)陷盆地内的白垩纪红色碎屑岩以外，广泛发育元古代、古生代地层，沉积了巨厚的碎屑岩类夹碳酸盐岩。浙西北区地质构造复杂，断裂皱褶发育。浙东南则分布大片的中生火山岩，仅局部夹沉积岩，构造以断裂为主。在一些白垩纪断陷盆地发育红色粉砂岩、砂岩、砾岩等。部分地区为第三纪玄武岩所覆盖。许多规模不等的中酸性岩体侵入于火山岩中。沿江山─绍兴断裂两侧局部出露有前寒武纪变质岩。

地层岩石常被断裂切割，岩石的破碎程度以及风化层厚度等变化很大。几乎所有斜坡都为厚度和组成变化很大的残(坡)积层所覆盖，属于滑坡易发地区。

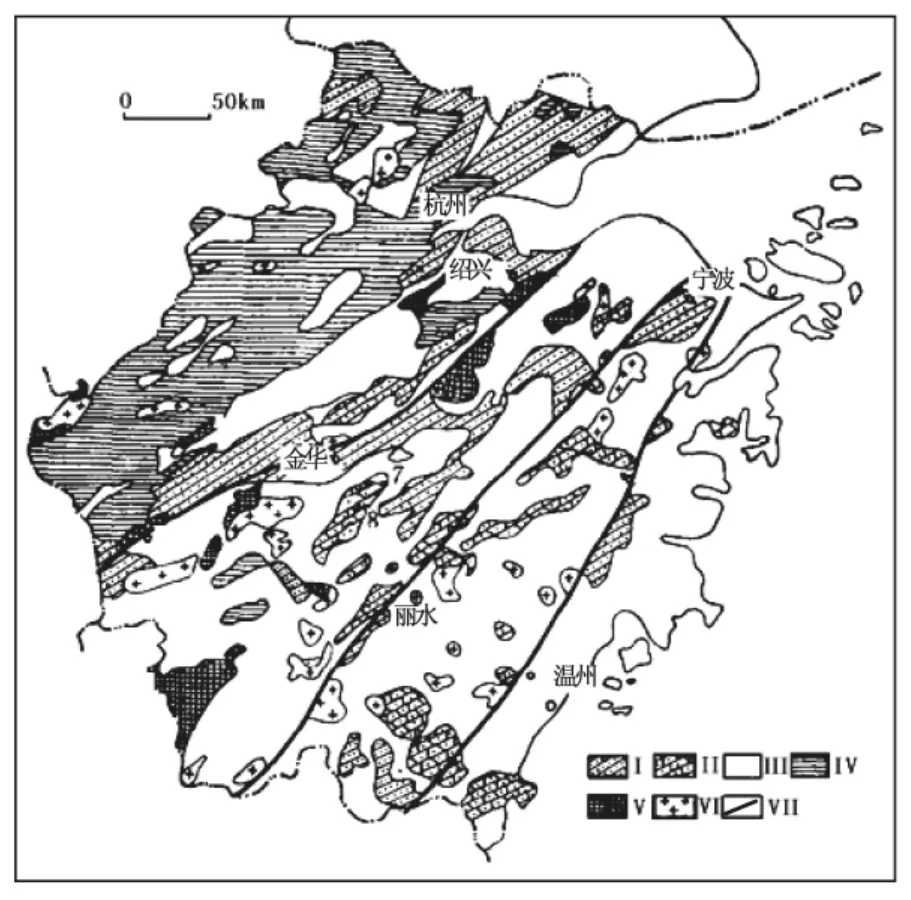
图2 浙江省地质略图。Fig.2 Schematic geological map of Zhejiang Province

浙江省属亚热带季风气候区。平均年降水量在1000～1900mm。但是受季风气候和地形影响，降水量年内分配不均匀，一般在5～9月的降雨量占全年水量的60%以上。特别是在夏季，受热带气旋(台风)影响常发生暴雨，绝大部分暴雨都出现在5～9月期间。由于降雨受到地形的强烈影响，来自一次暴风雨或给定年份内的降水量在很短距离内就变化很大。

由于地理位置、地质和地形的原因，浙江每年都会遭受暴雨袭击。暴雨往往引发大量浅层滑坡，对公众生命和经济造成严重危害。自1990年以来，在每起严重的滑坡之后，浙江省地质矿产厅通常都会立即派遣有经验的地质人员去现场调查，记录下滑坡发生日期和位置、滑坡类型和规模以及造成的经济损失和人员伤亡等情况。特别是在2000～2003年期间，浙江省国土资源厅实施了对全省45个丘陵和山区县的滑坡灾害野外调查计划。在这次调查计划之后建立了滑坡数据库，其中，既有发生日期(时间)又有坐标记录的滑坡为1414个(图1)。

浙江省水文勘测局在浙江设有一个由1257个雨量站组成的监测网，基本覆盖浙江全部陆地区域(图3)。在本次研究中主要使用上述的1414个有明确日期和坐标记录的滑坡数据。从1257个雨量站在1990年至2002年期间的雨量观测记录中均可查询到对应的日降雨量数据。由于滑坡并不一定都发生在雨量观测站点处，对于这种情况，我们采用距离滑坡发生点最近的观测站记录的雨量数据作为该处的降雨量值。

图3 由浙江省水文局管理的雨量站网分布图Fig.3 Location of automatic rain-gauges

2 滑坡发生频度与降雨历时的关系

在这里，我们把降雨事件定义为前、后各24h内降雨小于4 mm的一场连续降雨。按照这个定义，分析了1990～2003年期间不同历时的降雨事件对滑坡发生的影响。观测的降雨事件历时范围从滑坡当天至前15d。如图4所示，在所统计的1414处滑坡中，有71.3%由历时为一天的降雨引发，与2d和3d降雨有关的滑坡分别占总数的6.9%和5.7%，只有不足3%的滑坡与历时超过10d的降雨有关。由此可见，在浙江发生滑坡主要与当日的短历时强降雨有关。

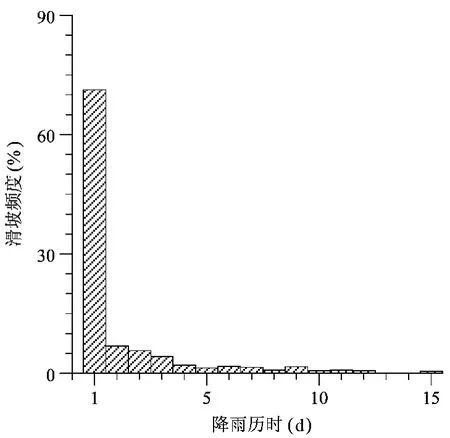
图4 浙江1990～2003年期间发生的1414个滑坡与降雨事件历时(d)的关系Fig.4 Histogram showing the frequency distribution of landslides versus rainfall event with different durations from 1 to15 days during the period 1990 to 2003，Zhejiang，China.

由以上所述可知，在浙江与历时超过10d的降雨事件有关的滑坡很少，因此这里主要考虑滑坡当日和前10d内的降雨情况。我们使用4个时间段的累计降雨来考察滑坡频度与降雨量的关系:(a)滑坡当天降雨(1d);(b)当日降雨加上3天前期降雨(4d); (c)当日降雨加上5天前期降雨(6d);(d)当日降雨加上10天前期降雨(11d)。这里所说的前期降雨是指滑坡发生当日之前一个给定时间段内的累计降雨。图5表示滑坡频度与不同时段累计降雨的关系。该图表明，对于所考虑的4种情况，在累计降雨小于200 mm时发生的滑坡占1414个滑坡的65%以上，有25%左右的滑坡是在累计降雨为200～500 mm时发生的，当累计降雨超过500 mm时只有不足10%的滑坡发生。这种情况似乎是违反直觉的。但是，如果考虑到日降雨量的分布就不难理解了。如图6所示，在1257个雨量站从1990～2003年这14年期间日降雨量记录中，日降雨量超过250mm的天数仅占总降雨天数的0.07%，而日降雨量超过5000mm的天数就更少了(只有16d，占总降雨天数的0.001%)，以至于与这些降雨事件有关的滑坡也不多。另一方面，在一次降雨过程中，在一些有坡积或残积物覆盖的斜坡处，当降雨超过滑坡发生的某个临界雨量时，如果潜在滑坡的大多数都已经发生了，那么即使后续的降雨量增大也可能仅仅引发少量滑坡。

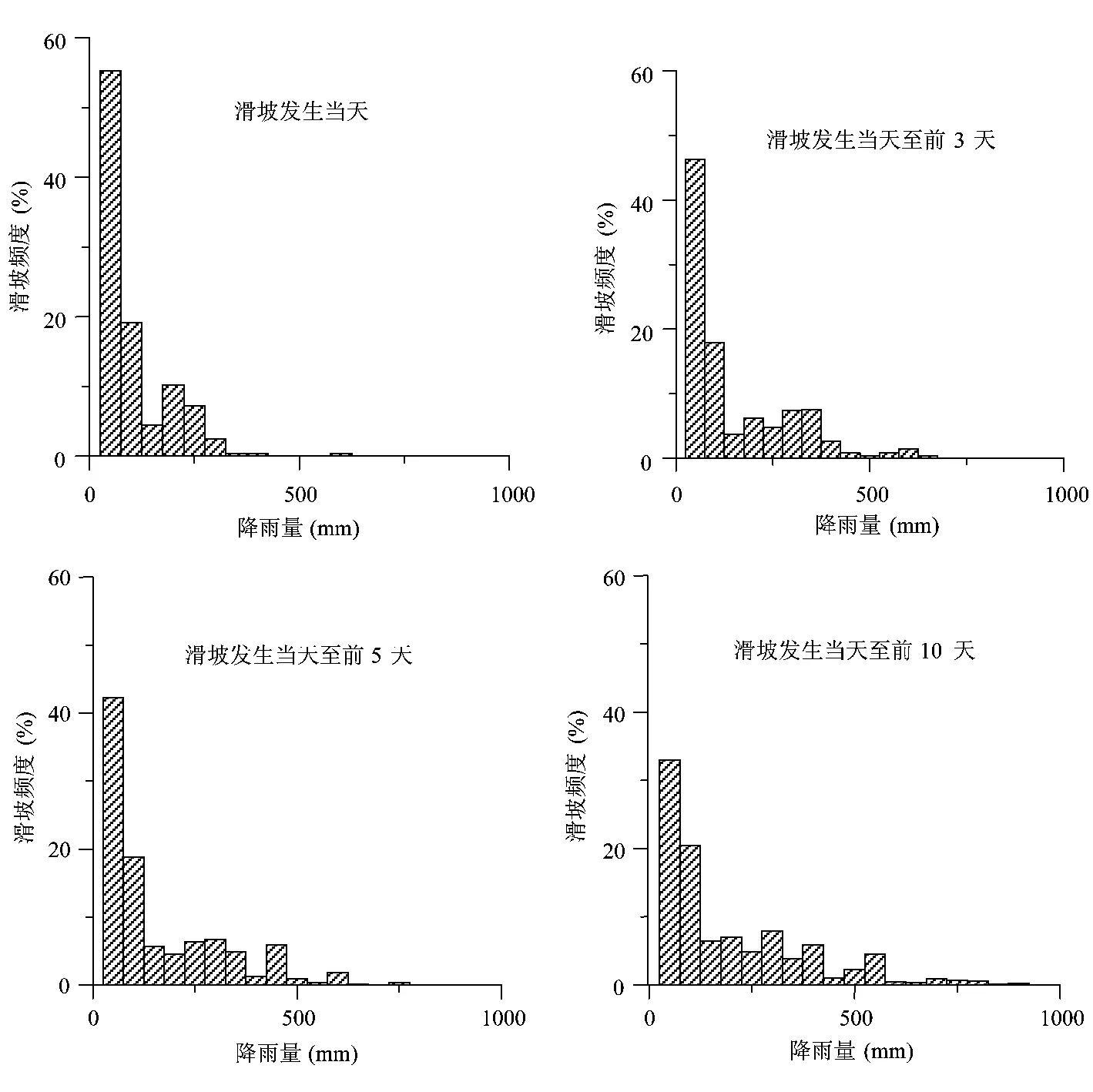
图5 浙江1990～2003年期间在不同时段内累计降雨与滑坡频度分布的关系Fig.5 Histogram showing the frequency distribution of landslides for the cumulative rainfall within different time intervals during the period 1990 to 2003，Zhejiang，China.

3 基于滑坡频度－降雨量分形关系的区域降雨阈值

从图5可以看出，滑坡频度与降雨量之间的关系可能遵循一种分形的幂指数分布。一般，分形分布可以表示为:

式中:p(x)——具有特征线度为x的物体的数目;

C——比例常数，标度指数D可以是分数，在分形几何学中称D为分形维数或分维，它是描述一个分形的最基本的特征量。

对于自然现象，由式(1)定义的分形关系一般只能在一定的尺度范围内成立，这个范围称为无标度区。

式(1)定义的分形分布是将事件发生频度作为它大小的一个函数，即x是对事件大小的度量。如果从一个广义的角度来理解分形分布，则x也可以是对与事件有关的某个变量(例如引发滑坡的降雨量)大小的度量。因此，作为对式(1)应用的一个推广，可以将滑坡发生频度作为引发滑坡的降雨量的一个函数。我们先定义一个概率密度函数l(R)为:

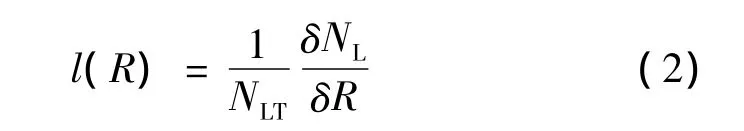
式中:δNL——在降雨量从R到R+δR时发生的滑坡数;

NLT——所考虑的滑坡总数。

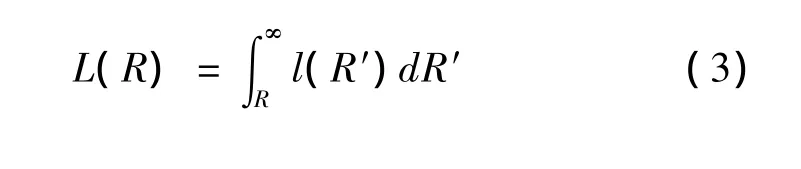
图6 浙江地区1990～2003年期间的日降雨量分布直方图Fig.6 Daily precipitation distribution in Zhejiang during the period 1990 to 2003.The daily rainfall data obtained from the measurements of precipitation at 1257 rain-gauges

对于降雨量大于R时的滑坡发生概率L(R)可以写成:将式(2)代入式(3)并对其积分，可以得到滑坡累计频度与降雨量的分形分布关系

式中:C和β——由观测数据确定的常数。

在1990～2003年期间，浙江已知有明确发生日期和位置(坐标)的滑坡为1414个(即NLT=1414)，把降雨量大于R时的滑坡累计频度Lcf(＞R)和R标绘在双对数坐标图上(图7)，可以清楚看出，在所有4种情况中，滑坡累计频度随降雨量的变化均可以区分出两个不同的无标度区间，分别按照式(4)进行拟合得到两条具有不同斜率(标度指数β)的直线，表明滑坡累计频度作为降雨量的函数遵循两个幂指数分布。

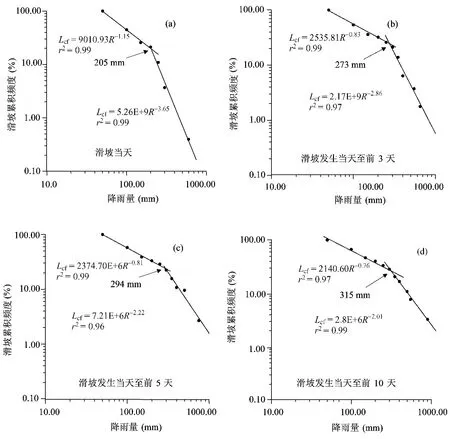
图7 浙江1990～2003年期间在不同时段内累计降雨与滑坡累计频度分布的关系Fig.7 Relationship between the cumulative frequency of landslides(Lcf)and the cumulative rainfall(R)of different time intervals during the period 1990 to 2003，Zhejiang，China.The distributions are well characterized by Lcf(＞R)∝R-βwithin two scale ranges.

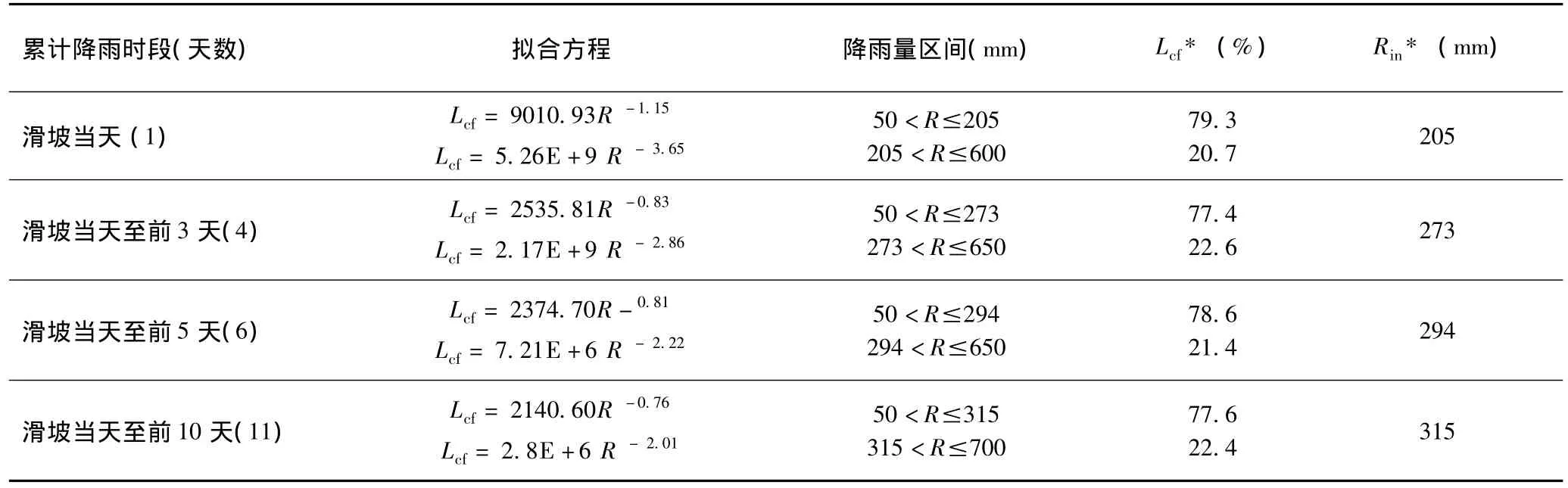
表1 累计滑坡频度-降雨关系的分形分布统计结果Table 1 Results of power-law distribution statistics for rainfall/landslides relationship

对于滑坡发生当天的日降雨(图7a)，在50mm＜R≤205mm范围内拟合直线的斜率为1.15，在205mm＜R≤600mm内拟合直线的斜率为3.65。当考虑的时段为滑坡当天至前3天时(图7b)，在降雨为50mm＜R≤273 mm范围内拟合直线的斜率为0.83，在273mm＜R≤650mm内拟合直线的斜率为2.86。对于滑坡当天至前5天这个时段(图7c)，在降雨为50mm＜R≤294mm范围内拟合直线的斜率为0.81，在294mm＜R≤650mm内拟合直线的斜率为2.22。对于滑坡当天至前10天这个时段(图7d)，在降雨为50mm＜R≤315mm范围内拟合直线的斜率为0.76，在315mm＜R≤700mm范围内拟合直线的斜率为2.01。

由于Lcf是对降雨量大于R时的滑坡累计频度统计，因此对于图7中的4种情况，在两条直线交点处的Lcf值均指示了降雨量在50mm＜R≤Rin时的滑坡累计频度是73.7%～80.4%(这里Rin表示拐点处的降雨量)，平均为76.7%。当降雨量超过Rin后，滑坡的累计频度仅为19.6%～26.3%(平均23.3%)。据此，可以把对应于拐点的降雨量Rin定义为引发滑坡的累计降雨阀值的上边界(以THCR表示)。对于降雨型滑坡，当一地区的累计降雨达到THCR值，就可能在该地区引发大部分滑坡。在浙江，对于1d、4d、6d 和11d这4个时间段的累计降雨情况，引发75%左右滑坡的累计降雨阀值THCR分别为205mm(1d)、273mm(4d)、294 mm(6d)、315 mm(11d)。表1概括了对4种情况的累计滑坡频度－降雨关系的分形分布统计结果。

以上讨论了滑坡频度与日降雨分布的关系，如果考察小时降雨分布(即降雨强度，以mm/h表示)，那么滑坡的频度与降雨强度之间是否仍然遵循分形关系呢?由于有关滑坡发生时间的记录非常少，目前还缺乏足够的样本来做这样的分析。

4 结论

本文研究表明，降雨引发滑坡的累计频度与日降雨量之间遵循分形的幂指数关系，并且在两个尺度的降雨量范围内具有不同的标度指数，对应于拐点的降雨量Rin定义了引发滑坡的累计降雨阀值的上边界(以THCR表示)。对于降雨型滑坡，当一地区的累计降雨达到THCR值，就可能在该地区引发大部分滑坡。对于浙江地区，引发75%以上滑坡的累计降雨阀值分别为205mm(1d)、273mm(4d)、294 mm(6d)、315 mm(11d)。

降雨引发滑坡与降雨下渗导致岩土体内的孔隙压力增大有关，而岩土体中的裂隙和孔隙分布一般是分形的，由此可以推测与降雨有关的孔隙压力的分布可能也是分形的，并由此导致降雨引发的滑坡在空间分布上以及滑坡的频度与降雨量大小之间的关系也遵循分形分布。然而，目前尚不清楚为什么滑坡频度─降雨量分布的分形关系显示两个具有不同标度指数的无标度区间，看来要真正理解隐藏在这种分形关系背后的物理机制还有待于进一步的研究。

［1］李长江，麻土华，朱兴盛.降雨型滑坡预报的理论、方法及应用［M］，北京:地质出版社，2008.

［2］Caine，N.，The rainfall intensity－duration control of shallow landslides and debris flows［J］，Geografiska Annaler，1980，62A(1－2):23–27.

［3］Wieczorek，G.F.，Effect of rainfall intensity and duration on debris flows in central Santa CruzMountains［A］.In:Debris flow/avalanches:process，recognition，and mitigation(Costa，J.E.，Wieczorek，G.F.，eds).Geological Society of America，Reviews in Engineering Geology，1987(7):93–104.

［4］Cannon，S.H.，1988.Regional rainfall－threshold conditions for abundant debris－flow activity［A］.In:Landslides，Floods，and Marine Effects of the Etorm of January 3–5，in the San Francisco Bay Region，California (Ellen SD，Wieczorek GF，eds).US Geological Survey Professional Paper，1982，1434.35–42.

［5］Larsen，M.C.，Simon，A.，A rainfall intensity－duration threshold for landslides in a humid－tropical environment，Puerto Rico［J］.Geogr Ann A，1993，75(1－2):13–23.

［6］Wilson，R，C.，Wieczorek，G.F.，Rainfall thresholds for the initiation of debris flow at La Honda，California ［J］.Environ Eng Geosci，1995，1(1):11–27.

［7Glade，T.，Crozier，M.J.，Smith，P.Applying probability determination to refine landslide－triggering rainfall thresholds using an empirical“Antecedent Daily Rainfall Model”［J］.Pure Appl Geophys，2000，157(6/8):1059– 1079.

［8］Wieczorek，G.F.，Morgan，B.A.，Campbell，R.H.，Debris flow hazards in the Blue Ridge of Central Virginia ［J］.Environ Eng Geosci，2000，6:3–23.

［9］Aleotti，P.A warning system for rainfall－induced shallow failures［J］.Eng Geol，，2004，73:247–265.

［10］Guzzetti F.，Peruccacci S.，Rossi M.＆Stark C.P. Rainfall thresholds for the initiation of landslides［J］.Meteorology and Atmospheric Physics，2007，98(3－4):239 －267.

［11］Casadei，M.，Dietrich，W.E.，and Miller，L.Testing a model for predicting the timing and location of shallow landslide initiation in soil－mantled landscapes［J］，Earth Surface Processes and Landforms，2003，28:925–950.

［12］Finlay，P.J.，Fell，R.，Maguire，P.K.The relationship between the probability of landslide occurrence and rainfall［J］.Canadian Geotechnical Journal，1997，34:811–824.

［13］Dai，F.C.，Lee，C.F.，Frequency－volume relation and prediction of rainfall－induced landslides［J］，Eng.Geol. 2001，59:253–266.

Abstract:This paper studied the relationship between the landslide occurrences and the rainfall level based on 1414 landslides from field survey and daily rainfall data corresponding to the date of the landslide occurrence during 1990－2003 in Zhejiang Province，China.The results showed that the cumulative frequency of the landslide occurrence correlates well with the landslide－triggering rainfall and can be described using two power－law relations with different scaling exponents for two different ranges of the rainfall level.The rainfall level corresponding to the intersection point of two fitted correlation lines may be defined as the cumulative rainfall threshold(THCR)that defines the upper－bound rainfall thresholds for triggering shallow landslides;a large number of landslides may be induced when the amount of cumulative rainfall comes to the THCRvalue.For the cumulative rainfall in four time intervals considered(1，4，6 and 11 days)，the THCRfor triggering about 75%of landslides in the study region is 205mm for 1 day，273mm for 4 days，294 mm for 6 days，and 315 mm for 11 days，respectively.

Key words:landslides;regional rainfall thresholds;power law distributions;fractals

Fractal relation of landslide frequency and rainfall

LI Chang－jiang1，MA Tu－hua1，LI Wei2，ZHENG Ai－ping3，ZHU Xing－sheng1
(1.Zhejiang Information Center of Land and Resources，Hangzhou310007，China; 2.Zhejiang Provincial Department of Land＆Mineral Resources，Hangzhou310007，China; 3.Department of Earth Sciences，Zhejiang University，Hangzhou310027，China)

1003－8035(2010)01－0087－07

P642.2

A

2009－10－30;

2009－12－14

李长江(1951—)，男，重庆人，教授级高级工程师，主要从事矿产地质和灾害地质研究。

E－mail:zjigmr@mail.Hz.zj.cn