基于广义Hoek-Brown准则边坡稳定性分析强度折减法

陈昌富，翁敬良

(湖南大学岩土工程研究所，湖南长沙 410082)

基于广义Hoek-Brown准则边坡稳定性分析强度折减法

陈昌富，翁敬良

(湖南大学岩土工程研究所，湖南长沙 410082)

目前的强度折减法大多基于Mohr－coulomb准则，而较少基于Hoek－Brown准则。为了在Hoek－Brown准则中实施强度折减法，并使其得到的结果与Mohr－coulomb准则中强度折减法得到的结果等效，本文利用Hoek－Brown准则参数m、s、σci与粘结力c和内摩擦角φ之间的关系，在Hoek－Brown准则中同时对m、s实施强度折减，通过理论推导得到m、s折减系数之间的关系;并进一步推导得到m、s折减系数与基于Mohr－coulomb准则强度折减系数之间的关系;最后，由FLAC3D软件建立计算模型，采用所确定的折减方法计算边坡的安全系数，并将该结果与极限平衡法所得到计算结果进行比较，结果表明:本文确定的折减方法与极限平衡法所得到的安全系数的相差仅1.76%，验证了本文所确定的强度折减法的可行性。

Hoek－Brown准则;Mohr－coulomb准则;强度参数;极限平衡法;FLAC3D软件

0 引言

Hoek－Brown强度准则是可以估计完整岩石或节理岩体剪切强度的半经验准则［1］。经过20余年的发展，5次较大的改进［2－7］，它已成为岩体强度预测及稳定性分析领域应用最广泛的准则之一，并在极限平衡法中已经得到广泛应用［8－10］。

强度折减法是一种边坡稳定性分析重要方法，其原理是逐渐折减边坡的强度参数，直到临界失稳状态，此时所对应的折减系数即为边坡的整体安全系数。目前，强度折减法主要针对Mohr－coulomb准则进行实施，即对抗剪强度参数粘结力c、内摩擦角φ进行折减，从而得到边坡的安全系数［11］。但Mohrcoulomb准则对岩体强度的描述有一定局限性，如不能解释低应力区对于岩体的影响，只能反映岩体的线性破坏特征等［12］。Hoek－Brown经验强度准则则能够反映岩体的固有特点和非线性破坏特征，弥补了Mohr－coulomb准则的不足，符合边坡岩体的变形特征和破坏特征［13－14］。文［11］认为在强度折减的过程中，Hoek－Brown强度准则参数m、s、σci的折减系数满足K2m=Ks，Kσ=1。

本文利用Hoek－Brown准则参数m、s、σci与粘结力c和内摩擦角φ之间的关系，在Hoek－Brown准则中同时对m、s实施强度折减，通过理论推导得到m、s的折减系数之间的关系。并进一步推导得到m、s的折减系数与基于Mohr－coulomb准则强度折减系数之间的关系，从而使本文所确定的强度折减法得出的安全系数能够用基于Mohr－coulomb准则强度折减法所定义的安全系数K来表达。最后，在算例中用FLAC3D软件建立计算模型，采用所确定的折减方法计算边坡的安全系数，并将该结果与极限平衡法计算所得到的结果进行比较，验证所确定的折减方法是可行的。

1 Hoek－Brown强度准则

1.1 Hoek-Brown强度准则简介

Hoek－Brown强度准则的特点之一是实现了以一定的数学方式对岩体应力分量进行规则化，并使之与岩体材料属性相联系。同时，广义Hoek－Brown屈服准则既可表示为主应力形式，也可表示为破坏面上的正应力和剪应力形式，因此可以十分方便地用于屈服面的强度估计，比如边坡的潜在破坏面的确定等［15］。

Hoek－Brown屈服准则定义了岩体产生破坏的最大和最小主应力关系，对于完整岩石有［1］:

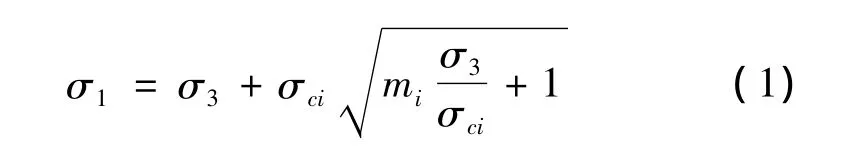
式中:σci——岩石单轴抗压强度;

mi——完整岩石经验常数，与岩石类型有关，主要反映岩石的软硬程度，取值为5～40，岩石越硬取值越大。

岩体破坏时的最大和最小主应力满足［5］

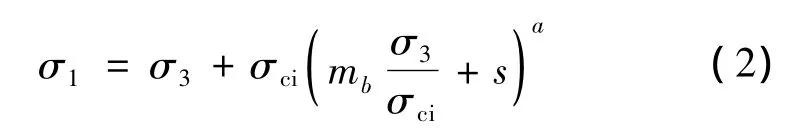
式中:mb、s、a为与岩体节理等不连续面有关的参数，均可表述为如下RMR的函数。

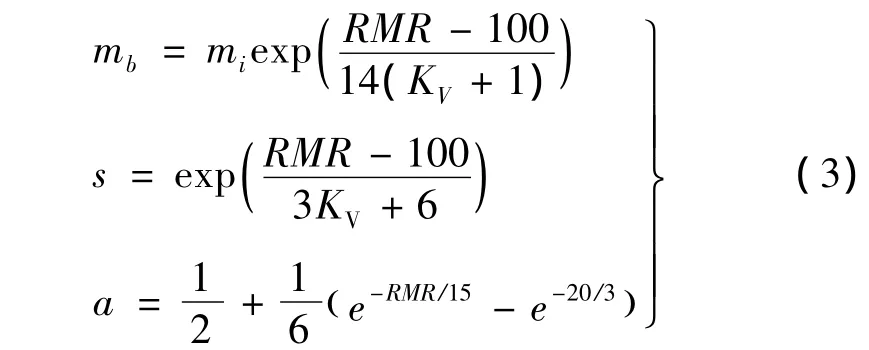
式中:RMR值是根据岩块的单轴抗压强度、岩芯的RQD值、节理间距、节理条件、地下水的作用等5个方面的因素对岩体质量指标进行综合评价来确定的，适合于大多数岩体。KV为岩体完整性系数，一般通过测试岩石和岩体中弹性波速度的办法确定［16］:当KV=1时，岩体未受扰动，Km=28，Ks=9;当KV=0时，岩体受到强烈扰动或比较破碎，Km=14，Ks=6。

1.2 FLAC3D中的Hoek-Brown模型

1.2.1 基本方程

对于Hoek－Brown模型，假设岩体当前的主应力为(σ1，σ2，σ3)，初始试验应力(σt1，σt2，σt3)通过增量弹性理论计算［17］

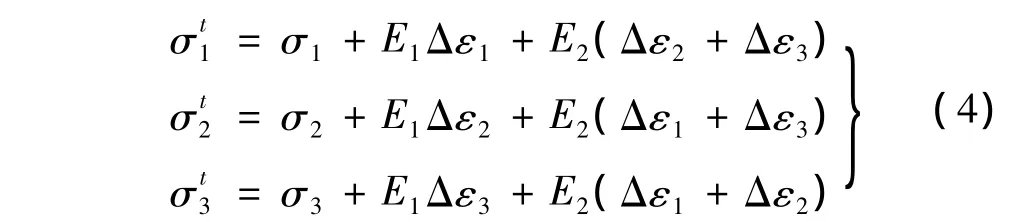
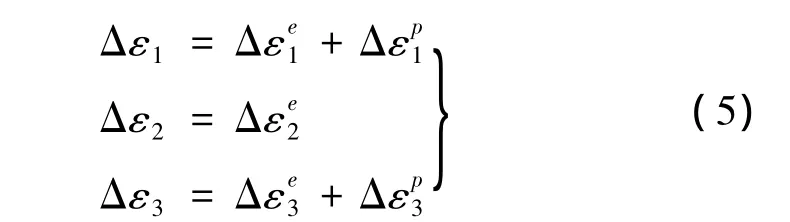
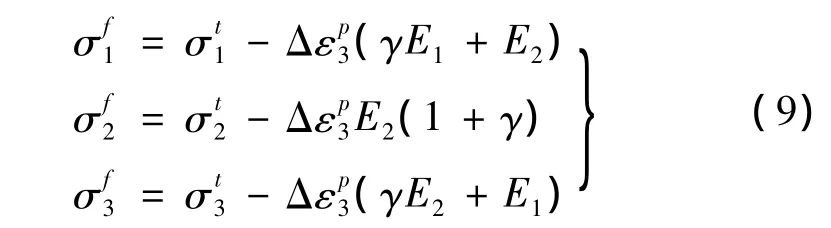
在屈服阶段，式(2)由最终应力满足，即

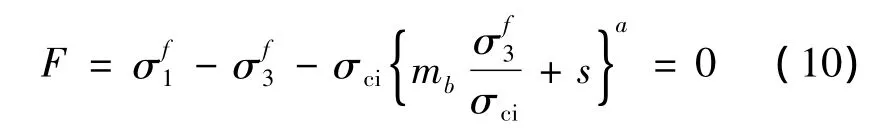
1.2.2 流动法则

需要考虑一个合适的流动法则，它能描述屈服阶段材料的体积特性。通常，流动参数γ将取决于应力，且可能取决于应力历史。在围压很低或拉应力状态下，因为代表性的破坏模式是轴向劈裂而不是剪切，所以提材料的“剪胀角”是没有意义的。尽管体积应变以一种复杂的方式与应力水平相关，有下面几种情况:

(1)相关联的流动法则

许多岩石在无侧限压缩条件下屈服时表现出很大速率的与轴向劈裂及楔形破坏有关的体积膨胀。相关联流动法则提供理论上可以证明的最大体积应变率。此流动法则有望应用于单轴应力状态(σ3= 0)的附近区域。相关联流动法则，其塑性应变率的张量与屈服面正交。因此有:

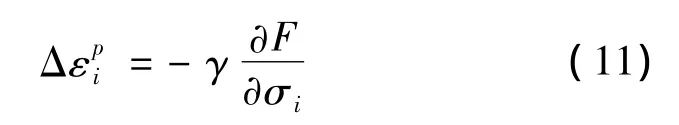
式中下标表示主应力方向上的分量，F由式(10)定义，对该表达式求导数，并用式(8)，有

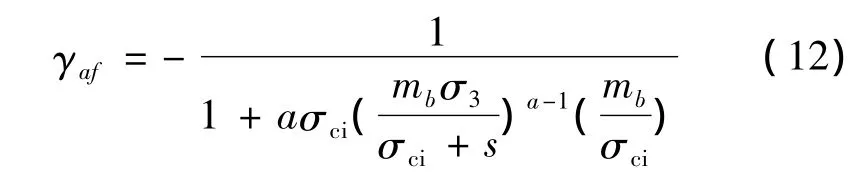
(2)径向流动法则

在单轴拉伸条件下，我们也许期望材料将在拉伸应力方向上发生屈服。如果施加的拉应力是各向同性的，假定材料将各向同性变形。这两种状态通过径向流动法则实现，假定所有主应力都是拉应力时使用径向流动法则。对于一个同主应力张量共轴的流动速率张量，有

(3)恒定体积流动法则

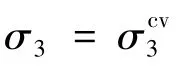
(4)复合流动法则

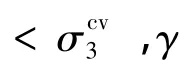
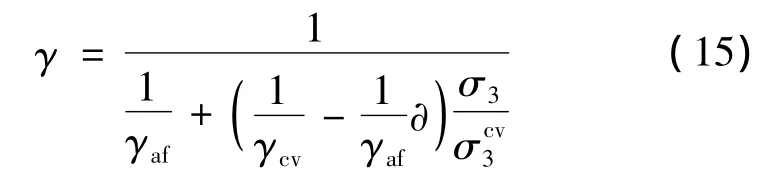
最后，当σ3＞σcv3时，使用体积恒定的值γ=γcv。如果σcv

3为零，则模型状态接近零剪胀角的非关联流动法则。如果σcv3为一个相对σci大得多的值，模型状态接近于相关联流动状态。

2 Hoek－Brown准则中强度折减法

2.1 m、s、σci与c和φ的关系

将Hoek－Brown准则和Mohr－Coulomb准则进行对比。在确定m、s和σci后，可利用式(2)得到岩体力学参数。

岩体单轴抗压强度为:

岩体单轴抗拉强度为:

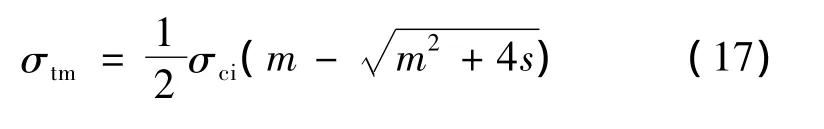
Mohr－Coulomb准则的表达式为:

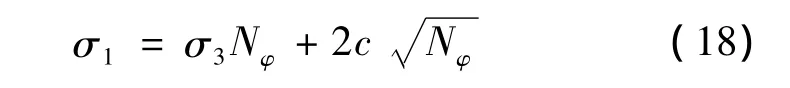
式中:Nφ=1+sinφ/1－sinφ，c和φ分别为粘结力和内摩擦角。

根据与Hoek－Brown准则对应的Mohr－Coulomb准则，可求得岩体的粘结力c和内摩擦角φ［18－19］:

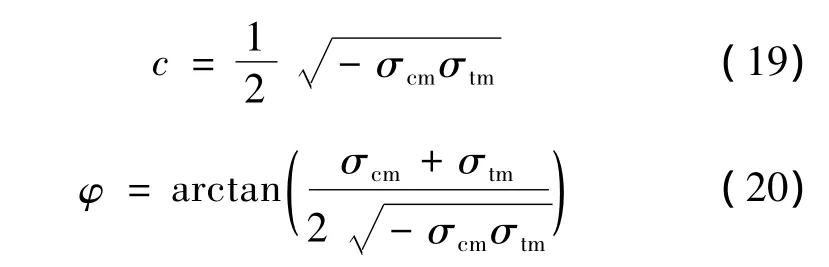
联立式(19)和(20)得m、s、σci与c和φ之间的关系为:

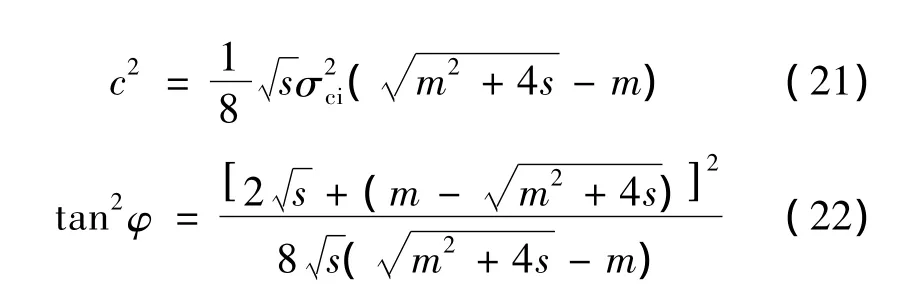
2.2 m和s的折减方法

假设边坡处于原始状态时，其参数为c0、φ0、m0、s0和σci;处于临界失稳状态时，其参数为ccr、φcr、mcr、scr和σci。且假设:

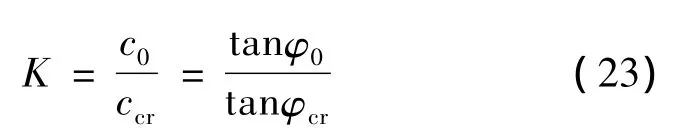
其中K为基于Mohr－coulomb准则的强度折减系数，当边坡达到临界失稳状态时，其K即为边坡整体安全系数。又假设:

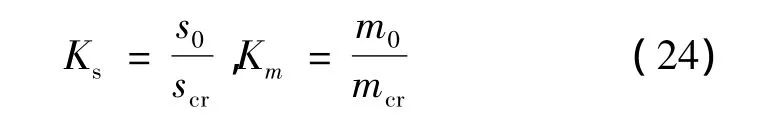
其中Ks、Km分别为基于Hoek－Brown准则的s、m的强度折减系数。

联立式(21)、(22)和(23)得:

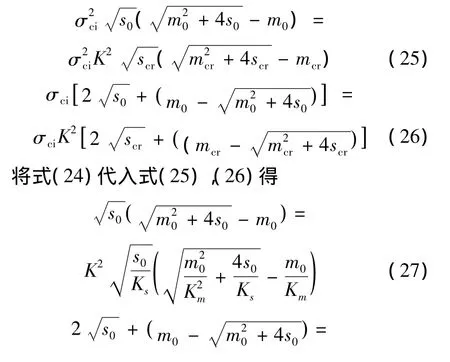
其中R，T为与Ks、Km无关的常数。将式(30)代入式(29)可得

将边坡处于极限平衡状态下的Ks、Km代入到式(27)或(28)即可得到边坡的安全系数K。其计算流程见图1。

3 算例与分析

3.1 算例

某均质软质岩石边坡，高20m，坡角45°，按照平面应变建立计算模型，模型共696个网格，790个节点。单元划分原则:坡面附近网格划分相对较密，周边部分较疏;y方向取一个单元宽度，并对模型中所有节点的y方向速度进行约束，以便等效地进行平面应变分析，计算尺寸如图2所示;边坡参数指标如表1所示:

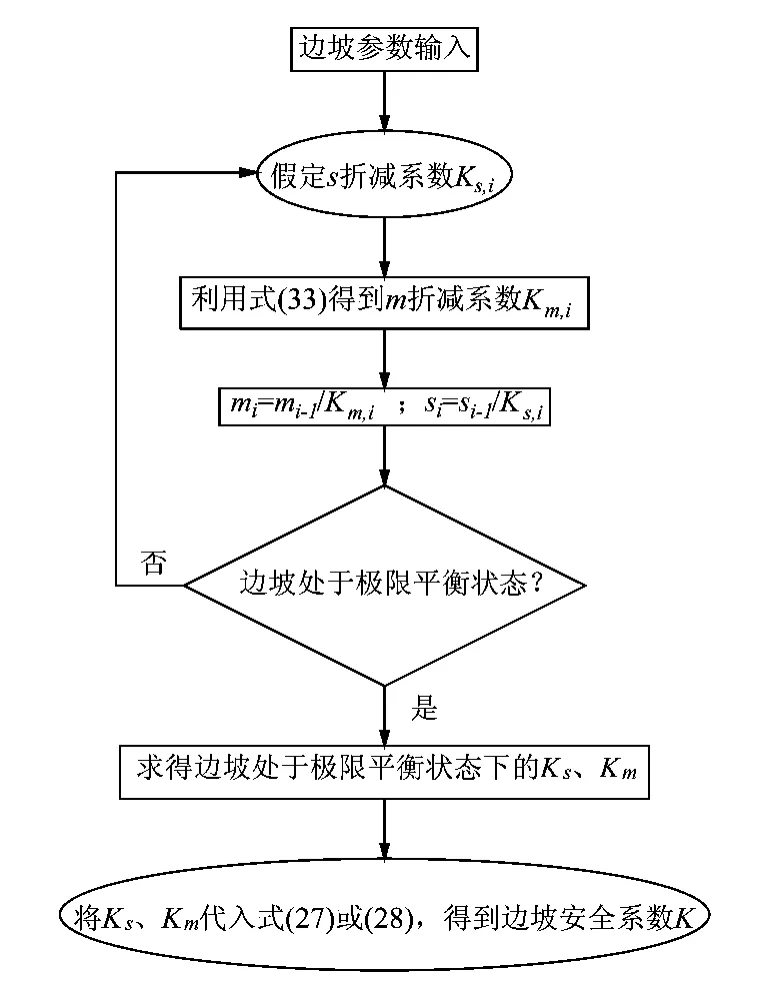
图1 安全系数求解流程Fig.1 Safety factor solving process

图2 岩石边坡几何关系Fig.2 Geometrical configuration of a rock slope

表1 边坡参数指标Table 1 Indexs of slope parameters

按照平面应变建立FLAC3D计算模型，边界条件为下部固定，左右两侧为水平约束，上部为自由边界，计算模型见图3。

3.2 结果分析

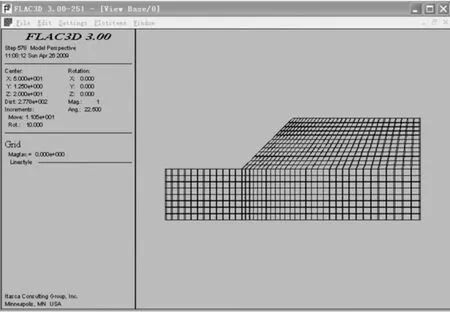
图3 边坡计算模型Fig.3 Slope calculation model

实施强度折减法的一个关键问题就是确定边坡失稳的判据，赵尚毅等［20］认为边坡达到破坏状态时，滑动体上的位移将发生突变，产生很大且无限制的塑性流动，程序无法找到一个既能满足静力平衡，又能满足应力－应变关系和强度准则的解，此时，不管从力的收敛标准判断，还是从位移的收敛标准来判断，计算都不收敛。因此，以静力平衡方程组是否有解、计算是否收敛作为边坡是否失稳的判据是合理的。

本文采用力不平衡比率ra(节点平均内力与最大不平衡力的比值)［21］是否大于10－5作为边坡是否失稳的判据，当ra＞10－5时，认为边坡已产生失稳破坏，否则认为边坡是处于稳定状态的。经计算求出边坡处于临界失稳状态时参数s折减系数Ks后，将Ks代入式(33)后即可得到参数m的折减系数Km，再将Km、Ks代入式(27)或(28)求得边坡的安全系数为:

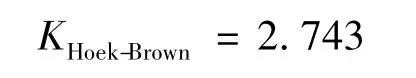
极限平衡法在边坡稳定性分析中已经得到了广泛的应用，在工程实践中已被证实为最有效的边坡稳定性分析方法之一。现将利用本文确定的强度折减法所求得的安全系数与陈祖煜基于Sarma法开发的岩质边坡稳定分析程序EMU所求得的安全系数做一比较，以验证本文所确定的计算方法的可行性。计算结果比较如表2所示:

表2 安全系数计算结果比较Table 2 Safety factors obtained by different methods and their errors

与极限平衡法计算结果相比，边坡安全系数相差不大，表明本文所确定的强度折减法正确可靠，可有效应用于节理岩质边坡的稳定性计算。

4 结语

(1)为了在Hoek－Brown准则中实施强度折减法，并使其得到的结果与Mohr－coulomb准则中强度折减法得到的结果等效，需要在Hoek－Brown准则中同时对m，s实施强度折减，通过理论推导得到了m、s折减系数之间的关系以及m、s折减系数与基于Mohr－coulomb准则强度折减系数之间的关系，从而使本文所确定的强度折减法得出的安全系数能够用基于Mohr－coulomb准则强度折减法所定义的安全系数K来表达。

(2)将本文确定的强度折减法计算出的安全系数与极限平衡法得到的安全系数对比，发现本文确定的折减方法与极限平衡法所得到的安全系数的差别仅1.76%，从而验证了本文所确定的强度折减法是可行的。

［1］HO EK E，Brown E T.Empirical strength criterion for rock masses［J］.J Geotech Engng Div ASCE，1980，106 (GT9):1013－1035.

［2］HOEKE.Strengthofjointedrockmasses［J］. Géotechnique，1983，33(3):187－223.

［3］HOEK E，BROWN E T.The Hoek－Brown failure criterion——a 1988 update［C］Proc 15th Canadian Rock Mech Symp，Toronto，Civil Engineering，University of Toronto，1988，31－38.

［4］HOEK E，WOOD D，SHAH S.A modified Hoek－Brown criterionforjointedrockmasses［C］ProcRock Characterization，Symp Int Soc Rock Mech:Eurock 92. London:Brit Geotech Soc，1992，209－213.

［5］HOEK E.Strength of rock and rock masses［J］.ISRM News Journal，1994，2(2):4－16.

［6］HOEK E，MARINOS P，BENISSI M.Applicability of the geological strength index(GSI)classification for very weak and sheared rock masses［J］.The Case of the Athens Schist Formation Bull Engg Geol Env，1998，57 (2):151－160.

［7］HOEK E，CARRANZA－TORRES C，CORKUM B. Hoek－Brownfailurecriterion－2002edition［C］HAMMAHW，BAWDENJ.CURRAN，＆M. TELESNICKI，Eds.Proceedings of NARMS－TAC 2002，Mining Innovation and Technology.Toronto:University of Toronto，2002，267－273.

［8］ROCSCIENCE Inc.Slide:2D limit equilibrium slope stability for soil and rock slopes，Verification Manual ［M］.Toronto Canada:Rocsience Inc.2003:6－26.

［9］李培勇，杨庆，栾茂田.Hoek－Brown岩石破坏经验判据确定岩石地基承载力的修正［J］.岩土力学，2005，26(4):664－666.

［10］CARRANZA－TORRESC.SomeCommentsonthe application of the Hoek－Brown failure criterion for intact rock and rock masses to the solution of tunnel and slope problems［C］BARLA G，BARLA M Eds.MIR 2004－XConferenceonRockandEngineeringMechanics. Torino.

［11］林杭，曹平，赵延林，等.强度折减法在Hoek－Brown准则中的应用［J］，中南大学学报(自然科学版)，2007，38(6):1219－1224.

［12］宋建波，刘唐生，于远忠.Hoek－Brown准则在主应力平面表示形式的讨论［J］.岩土力学，2001，22(1): 86－113.

［13］巫德斌，徐卫亚.基于Hoek－Brown准则的边坡开挖岩体力学参数研究［J］.河海大学学报，2005，33(1): 89－93.

［14］于远忠，宋建波.经验参数m和s对岩体强度的影响［J］.岩土力学，2005，26(9):1461－1468.

［15］吴顺川，金爱兵，高永涛.基于广义Hoek－Brown准则的边坡稳定性强度折减法数值分析［J］.岩土工程学报，2006，28(11):1976－1980.

［16］闫长斌，徐国元.对Hoek－Brown公式的改进及其工程应用［J］.岩石力学与工程学报，2005，24(22):4030－4035.

［17］刘波，韩彦辉.FLAC原理、实例与应用指南［M］.北京:人民交通出版社，2005，43－45.

［18］罗一忠，叶奥文.大厂91#矿体岩石力学参数工程处理［J］.江西有色金属，1998，12(3):9－12.

［19］Hoek E，Brown E T.Practical estimates of rock mass strength［J］.Int J Rock Mech Min Sci，1998，34(8): 1165－1186.

［20］赵尚毅，郑颖人，张玉芳.有限元强度折减法中边坡失稳的判据探讨［J］.岩土力学，2005，26(2):332－336.

［21］Itasca Consulting Group.Theory and background［M］. Minnesota:Itasca Consulting Group，2002.

Abstract:The present strength reduction method was mostly based on Mohr－Coulomb criterion other than.Hoek－Brown criterion.In order to use the strength reduction method in Hoek－Brown criterion and get a result equivalent to that by Mohr－Coulomb criterion，a new strength reduction method was applied to m and s simultaneously.The relationship between the reduction factors of m and s was obtained by theoretical deduction，based on the relationship among the parameters of m，s，σci and cohesion c，internal friction angle φ in Hoek－Brown criterion.The relationship between the factors of m and s in Hoek－Brown criterion and the reduction factors in Mohr－Coulomb criterion was found.In the end，a calculation model was built using FLAC3D application.The proposed reduction method was used in calculating the safety factor of slope，and the result was compared with that obtained by the limit equilibrium method.It showed the difference between them is mere 1.76%，which proved the feasibility of the reduction method proposed in the paper.

Key words:Hoek－Brown criterion;Mohr－Coulomb criterion;intensional parameter;limit equilibrium method; FLAC3D application

Strength reduction method based on generalized Hoek-Brown criterion for slope stability analysis

CHEN Chang－fu，WENG Jing－liang
(Geotechnical Engineering Institute of Hunan University，Changsha410082，China)

1003－8035(2010)01－0013－06

TU457;P642

A

2009－08－25;

2009－09－29

国家自然科学基金(50878082)

陈昌富(1963—)，男，湖南祁东人，教授，博士生导师，主要从事边坡与支挡结构、地基处理等研究。E－mail:cfchen@163.com