考虑随机时间的重置期权定价模型

刘 莹

(浙江商业职业技术学院基础部,浙江杭州310053)

考虑随机时间的重置期权定价模型

刘 莹

(浙江商业职业技术学院基础部,浙江杭州310053)

利用等价测度和鞅的方法,以外汇市场的波动率为重设点依据的情况下推导了随机时间重置期权中的欧式看涨期权的定价公式.

重置期权;随机时间;违约金

最早的单点重置型卖权由Gray和W haley[1]提出,国内的欧辉、王莉君、张寄洲[2-6]等人也对重置期权进行了一定研究.但是上述的研究始终没有对重设点的随机性进行讨论,都是停留在事先指定好重设点的前提条件下展开的讨论.该文针对传统重置期权模型的缺点,研究一种更具有随机性的期权模式——随机时间的重置期权模型.

1 模型的假设

设(Ω,F,(Ft)t≥0,P)为一个完备的概率空间,(Ft)t≥0是概率空间(Ω,F,P)上的一个对t递增的子σ-域,假设对随机变量的所有叙述几乎处处成立或几乎必然成立.E(X|Ft)表示随机变量X关于到时间t为止可获得的信息的条件期望.下面的随机变量都是定义在这一概率空间上的.同时假设在期权有效期内,市场没有任何交易费用和税收、无套利机会、交易能够连续地进行、允许卖空且标的资产的数量是可分的.

假设到期时间为T,原定履约价为K,期权买卖双方在事先约定:在期权到期日T之前,期权持有者有权利在任意时刻对期权进行重新设置履约价.假设重新设置履约价的时间为τ,τ是一个随机时间,则该期权到期价值X(T)表示如下:

其中D(τ)表示在T时刻期权的持有者还必须付给对方一定的现金作为解除原来约定的违约金(D(τ)是时间的函数).

假设St表示可交易的基本标的资产的价格,满足

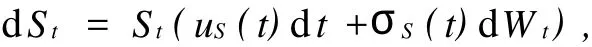
其中uS(t)和σS(t)为相应价格过程在时刻t的期望收益率和瞬时波动率,uS(t)和σS(t)是非随机函数(其中σS(t)大于零).{Wt,0≤t≤T}是P下标准的布朗运动.{Ft,0≤t≤T}是由Wt和W′t产生的自然σ-域,假设Wt与W′t是相互独立的,其中W′t表示一个P测度下另一个和Wt相互独立的标准布朗运动.

下面就以一种特殊的欧式看涨期权为例.设随机时间的重置欧式看涨期权的到期支付为X(T),则

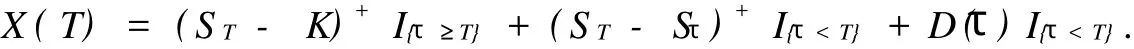
其中第一部分是期权双方不发生重新定价行为时的支付,第二部分为期权双方通过协商发生重新定价行为时的支付,第三部分是期权持有者与对方协商要求重新定价所需支付的违约金.

2 重新点的定义

根据美国芝加哥大学Tsay[7]所建立的随机波动率模型,建立了以随机波动率为依据选择重设点的随机时间的重置期权的定价模型.在此考虑选择债券市场、石油市场或外汇市场等非股票市场的波动率模型,主要的原因有两个.其一,如果直接选择股票市场的波动率作为重设点的依据,就容易给违约行为的发生带来一定的困难.例如在股票明显上涨的时候持有者想提出违约,另一方或者不愿意接受违约或者接受违约但提出更高要求的违约条件.其二,债券市场、石油市场或外汇市场等非股票市场和股票市场的价格波动存在着间接的联系,如上海交通大学管理学院的冯芸和吴冲锋用统计分析的方法说明了外汇市场的波动往往对股票市场的价格产生一种滞后的影响.如果可以从外汇市场的价格波动来预测股票市场的价格波动情况,对于股票的另一方来说就不会因为重设的理由太直接而反对违约或对违约行为提出更苛刻的违约条件.

假设外汇市场的波动率{ε(t)}服从dε(t)=-ε(t)(1-α)d t+σεd W′t,其中σε>0是非随机变量,并且假设|α|<1,使波动率的过程平稳.{W′t,0≤t≤T}是P下标准的布朗运动.则ε(t)=那么就满足一个随机微分方程Langevin方程,即ε(t)～

设τc=inf{t:ε(t)>c}表示波动率首次到达c的时刻,期权的持有者对卖出期权进行重新设置履约价;τd=inf{t:ε(t)≤d}表示波动率首次到达d的时刻,期权持有者就对买入期权进行重新设置履约价;通常投资者会选择组合期权进行投资,所以取τ=τc∧τd表示上述事件只要有一个发生就可以进行重新定价.

为了计算期权的定价公式,下面只研究当τ=τc时(或等价地d=-∞)的重新定价.

3 风险中性概率测度的转换

选择可交易的基本标的资产St,令Zt=e-rtSt.则d Zt=Zt(u-r)d t+Ztσd Wt,记

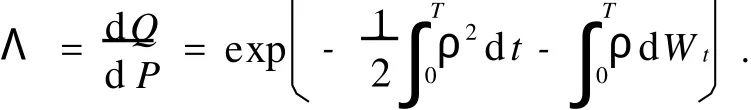
定义测度Q:d Q=Λd P,满足由Girsanov定理,可知PQ是P的等价鞅测度.且WQt=Wt+ρt,WQt是一个PQ测度下的标准布朗运动,在PQ测度下Zt满足:

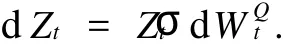
引理1 设在概率P下,X与Y,Ft分别独立,则 EQ(XY|Ft)=EQ(X)EQ(Y|Ft).

4 期权定价公式

定理1 设期权的到期日为T,期权买卖双方协商要重新设置履约价的时间为τ,随机时间的重置期权的欧式看涨期权在t时刻的价格为:

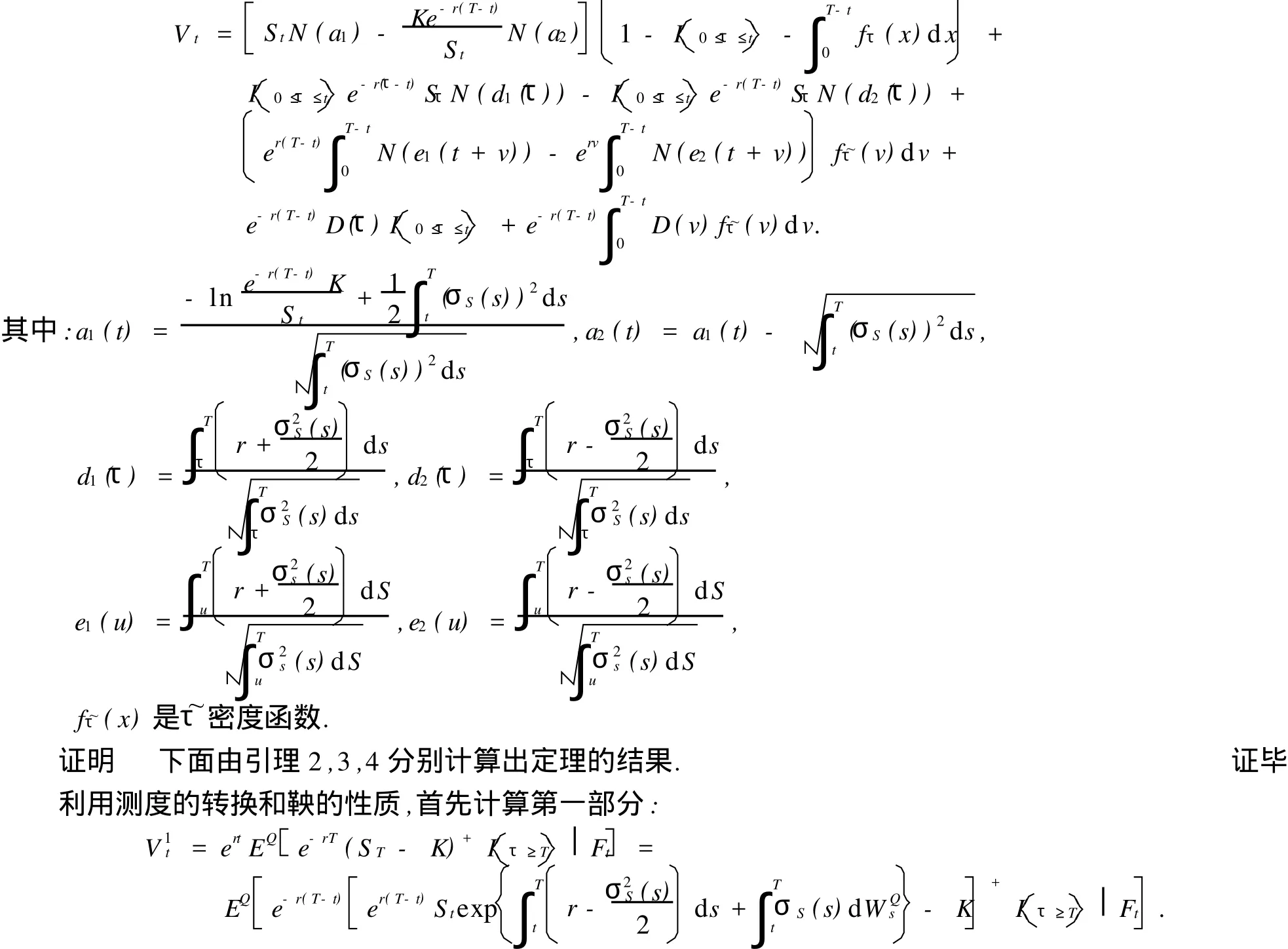
引理2 假设期权的到期日为T,期权买卖双方协商要重新设置履约价的时间为τ,则随机时间的重置欧式看涨期权持有者与对方协商要求重新定价所需支付的违约金的公式为:

由于三部分的求解方法类似,所以重点介绍第一部分的求解过程.下面直接给出第二部分和第三部分的两个引理.

引理3 设期权的到期日为T,期权买卖双方协商要重新设置履约价的时间为τ,则随机时间的重置

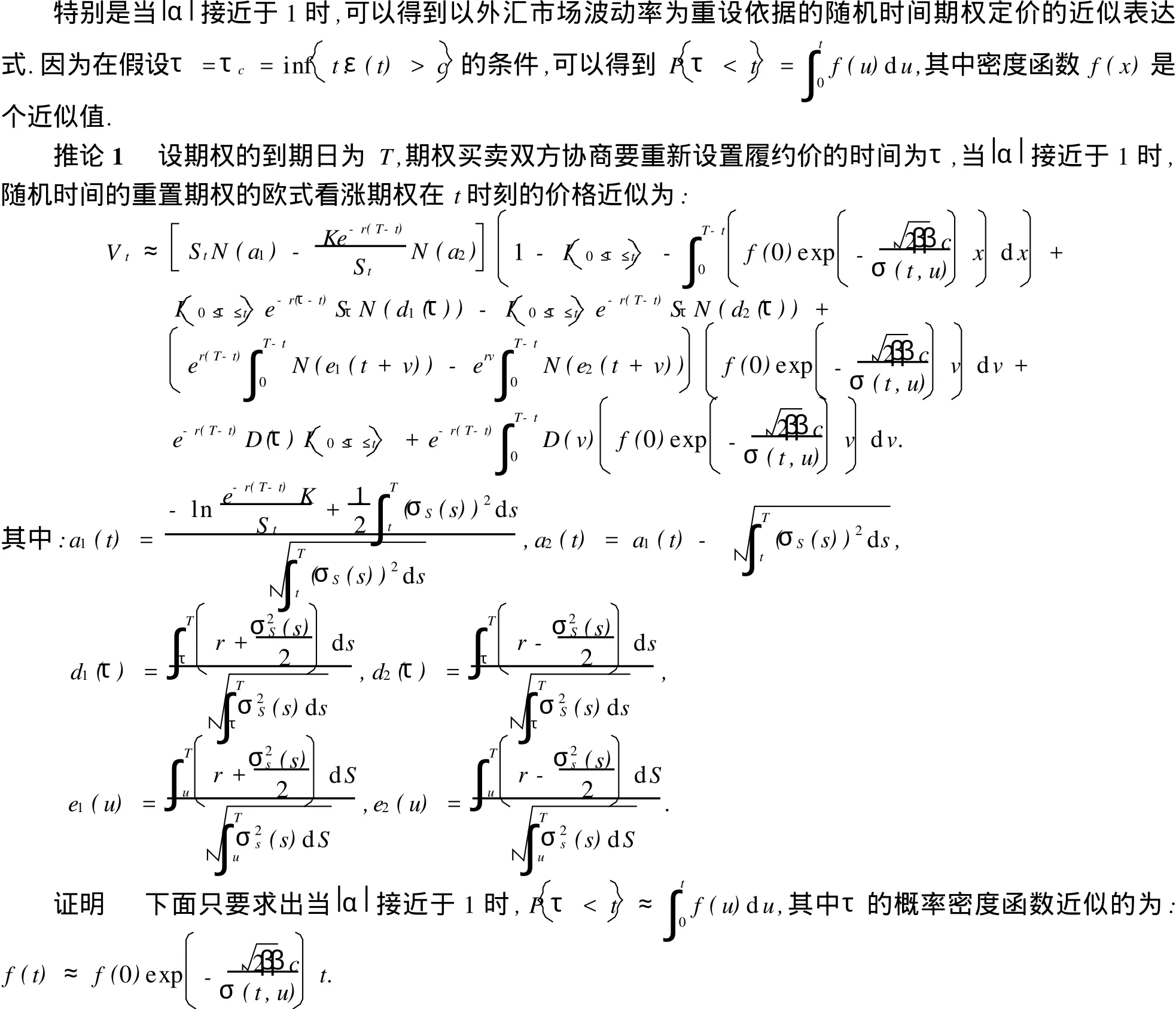
5 期权定价公式的近似解

[1]Gray S F,Whaley R E.Reset put options:valuation,risk characteristics,and an application[J].Australian Journmal of Management, 1999,24(1):1-20.

[2]刘平兵,欧辉.重置期权的一种创新及其定价[J].统计与决策,2006(10):32-34

[3]欧辉,向绪言,杨向群.重置期权的创新及其在随机利率情形下的定价[J].湖南文理学院学报,2004(3):6-10.

[4]王莉君,张曙光.随机利率下重置期权的定价问题[J].高校应用数学学报A辑,2002,17(4):471-478.

[5]朱海燕,张寄洲.随机利率下两类重置期权的定价问题[J].上海师范大学学报:自然科学版,2008,37(5):447.453.

[6]张寄洲,李松芹.重置期权的创新及其定价问题[J].上海师范大学学报:自然科学版,2008,37(5):441-446.

[7]Tsay R S.金融时间序列分析[M].潘家柱,译.北京:机械工业出版社,2006:329.

Reset Options M odel with Random Time

L IU Ying
(Department of Basic,Zhejiang Vocational College of Commerce,Hangzhou 310053,China)

Considering of the volatility of foreign exchange market,the paper derivates the p ricing formula of European call in reset op tions w ith random time by using equivalent measure and martingalemethods.

reset optionsmodel;random time;penalty

O211.6 MSC2000:91B28

A

1674-232X(2010)03-0209-06

DO I:10.3969/j.issn.1674-232X.2010.03.010

2010-02-21

2009年浙江省高校优秀青年教师资助计划(30202003).

刘 莹(1977—),女,浙江温州人,讲师,硕士,主要从事金融数学研究.E-mail:mengmeng0930@126.com