带误差项的广义Halpern-Mann型迭代序列的强收敛定理

余 静,谷 峰

(杭州师范大学理学院,浙江杭州310036)

带误差项的广义Halpern-Mann型迭代序列的强收敛定理

余 静,谷 峰＊

(杭州师范大学理学院,浙江杭州310036)

为证明Φ-伪压缩映象不动点的迭代收敛性,引进了带误差项的广义Halpern-Mann型迭代算法,并利用此迭代算法和一些分析技巧,证明了Φ-伪压缩映象不动点的一个新的强收敛定理.

Banach空间;Mann迭代序列;Halpern迭代序列;广义Halpern-Mann型迭代序列;Φ-伪压缩映象

1 引言和预备知识

定义4 设E为实Banach空间,称T:D(T)⊂E→E是Φ-强伪压缩映象,如果∀x,y∈D(T),存在j(x-y)∈J(x-y)和一个严格递增函数Φ:[0,∞)→[0,∞),Φ(0)=0,使得

近年来,许多学者致力用各种迭代算法去逼近非线性算子不动的研究,得到了许多好的结果[1-9].

1953年,M ann引进了一个迭代格式定义如下:

定义5[1]设E为实Banach空间,K是E的非空子集,T:K→K是一个算子,{αn}是[0,1]中的序列,则如下定义的序列{xn}∞n=0称为Mann迭代序列:

1998年,Xu引进了一个迭代格式定义如下:

定义6[2]设E为实Banach空间,K是E的非空子集,T:K→K是一个算子,{αn},{βn}和{γn}是[0,1]中的3个实数列,满足αn+βn+γn=1.则如下定义的序列{xn}∞n=0称为带有误差项的Mann迭代序列:

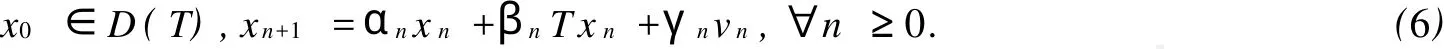
其中{vn}⊂D(T)是一个有界序列.

1967年,Halpern引进了一个迭代格式定义如下:

定义7[3]设E为实Banach空间,K是E的非空子集,T:K→K是一个算子,{αn}是[0,1]中的序列,则如下定义的序列{xn}∞n=0称为Halpern迭代序列:

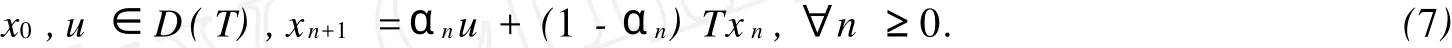
其中u∈D(T)是一个固定的点.

在此分别引进广义Halpern-Mann型迭代序列与带误差的广义的Halpern-Mann型迭代序列如下:

其中{αn′}∞n=0,{βn′}∞n=0,{γn′}∞n=0,{δn′}∞n=0与{αn}∞n=0,{βn}∞n=0,{γn}∞n=0,{δn}∞n=0,{σn}∞n=0分别是[0,1]中的满足一定条件的序列,且αn′+βn′+γn′+δn′=αn+βn+γn+δn+σn=1,{un}∞n=0是E中的有界序列.显然,式(5)是式(6)的特例,式(5)和式(7)都是式(8)的特例,式(5)、(6)、(7)、(8)又都是式(9)的特例.

文献[4]和[5]分别在Banach空间中研究了非扩张非自映象映象和伪压缩映象不动点的迭代收敛定理,文献[6]在半序线性空间中研究了一类非单调映射不动点的存在唯一性及其迭代收敛性.

文章使用带误差项的广义Halpern-M ann型迭代序列(9)去逼近Φ-伪压缩算子的不动点,证明了一个新的强收敛定理,所得结果改进、推广和统一了文献[7]和[8]的相关结果.

引理1[9]设E是实Banach空间,则∀x,y∈E,∀j(x+y)∈J(x+y),有

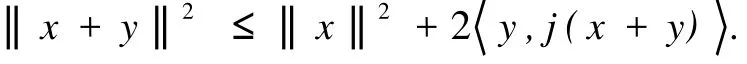
引理2[10]设Φ:[0,+∞)→[0,+∞)为严格递增函数,且Φ(0)=0,{θn},{ρn},{λn}为非负实序列,且满足若有θ2n+1≤θ2n-2λnΦ(θn+1)+ρn,∀n≥1,则lni→m∞θn=0.

2 主要结果

定理1 设E是实Banach空间,D为E的非空凸子集,映象T:D→D为一致连续、值域有界的Φ-伪压缩映象.设T的不动点集为F(T),设q为T的不动点,对任意给定的x0,u∈D,设{xn}∞n=0是由(9)所定义的具误差的广义Halpern-Mann型迭代序列,其中{αn},{βn},{γn},{δn}和{σn}是[0,1]中的5个实数列,且满足:因为{αn},{βn},{γn},{δn},和{σn}是[0,1]中且满足条件αn+βn+γn+δn+σn=1的实数列,所以由条件ii),iii)可知,∃N,当n>N时,有β2n+2βnγn≤1.从而式(14)可化简为

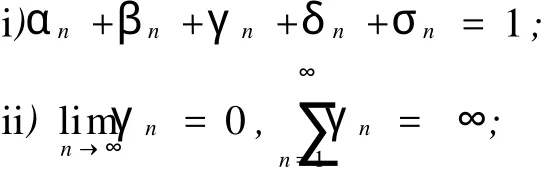
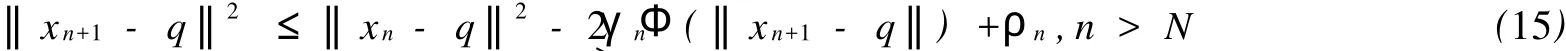
注 由于M ann迭代序列、具误差的M ann迭代序列、Halpern迭代序列和广义Halpern-M ann型迭代序列都是具误差的广义Halpern-Mann型迭代序列的特殊情况,因此文章结果对于迭代格式(5)、(6)、(7)、(8)也都成立.可见,文章结果统一、改进和发展了现有文献的一些相关结果.

[1]Mann W R.Mean valuemethods in iteration[J].Proc Amer Math Soc,1953(4):506-510.

[2]Xu Yuguang.Ishikawa and Mann iterative p rocessesw ith errors for nonlinear strongly accretiveoperator equtions[J].Math Anal Appl, 1998,224:91-101.

[3]Halpern B.Fixed points of nonexpanding maps[J].Bull Amer Math Soc,1967,73:957-961.

[4]傅秋平,谷峰.有限个渐进非扩张非自映象的强收敛定理[J].杭州师范大学学报:自然科学版,2008,7(3):172-176.

[5]陈军民,谷峰,何文明.Banach空间中一族伪压缩映象的收敛性定理[J].杭州师范大学学报:自然科学版,2009,8(3):184-188.

[6]路慧芹.半序线性空间中非单调算子不动点的存在性和唯一性[J].山东师范大学学报:自然科学版,2004,19(4):1-4.

[7]吕桂稳,薛志群.实Banach空间中带误差项的广义Mann迭代序列的收敛定理[J].河北师范大学学报:自然科学版,2009,33(5):585-588.

[8]Rafiq A.Mann iterative scheme for nonlinear equations[J].Mathematical Communications,2007,12:25-31.

[9]Petryshyn W V.A characterization of strict convexity of banach spaces and other use of duality mappings[J].J Funct Anal,1970,6: 282-291.

[10]Moore C,Nnolib V C.Iterative solutionsof nonlinear equations involving set-valued uniform ly accretive operators[J].Comput Math Appl,2001,42:91-105.

Strong Convergence Theorem of Generalized Halpern-Mann Type Iterative Sequence with Errors

YU Jing,GU Feng
(College of Science,Hangzhou No rmal University,Hangzhou 310036,China)

To p rove the iteration convergence ofΦ-pseudocontractive mapping fixed point,the paper has introduced the generalized Halpern-Mann type iterative algorithm w ith erro rs,and taking advantage of this iterative algorithm and some analysis techniques,it has p roved a new strong convergence theo rem ofΦ-pseudocontractivemapping fixed point.

Banach space;Mann iterative sequence;Halpern iterative sequence;generalized Halpern-Mann type iterative sequence;Φ-pseudocontractive mapping

O177.91 MSC2000:47H06;47H10;47H17

A

1674-232X(2010)03-0200-04

DO I:10.3969/j.issn.1674-232X.2010.03.008

2010-02-07

国家自然科学基金资助项目(10771141);浙江省自然科学基金资助项目(Y605191);杭州师范大学研究生教改项目;杭州师范大学研究生创新基金项目.

余 静(1986—),女,浙江慈溪人,应用数学专业硕士研究生,主要从事非线性泛函分析及其应用的研究.

＊通讯作者:谷 峰(1960—),男,辽宁沈阳人,教授,主要从事非线性泛函分析及其应用的研究.E-mail:gufeng99@sohu.com