隧道软弱围岩相似材料的力学性能试验
王抒,张顶立,房倩
(北京交通大学隧道及地下工程教育部工程研究中心,北京100044)
隧道软弱围岩相似材料的力学性能试验
王抒,张顶立,房倩
(北京交通大学隧道及地下工程教育部工程研究中心,北京100044)
基于相似理论和量纲分析法,将弹性模量作为铁路隧道软弱围岩的研究指标,推导出其相似指标.以重晶石、石英砂和凡士林等混合物作为铁路隧道软弱围岩的相似材料,通过应力控制式三轴试验仪进行常规三轴试验.并利用非线性回归分析的方法对实验结果进行分析,得出相似材料配比与弹性模量的变化规律.最后,给出估算这类相似材料中的重晶石等重要组分的含量与弹性模量的函数关系,以用于在实践中确定与隧道软弱围岩相适应的相似材料混合比.
软弱围岩;铁路隧道;弹性模量;相似材料;非线性回归
在隧道的开挖和支护过程中,需要涉及许多岩体强度破坏、变形失稳和加固处理等问题.对诸如此类的复杂问题,除了借助数学等工具进行理论分析外[1],还需借助岩土地质力学模型试验等手段进行解决[2-4].在隧道等模型试验的一些相关研究中,文[5]由相似理论出发,取隧道周围有限区域的岩体作为研究对象,确定了模型试验中的几何相似比和应力相似比.文[6]在各级围岩的众多物理力学指标中,选择弹性模量作为主要的决定因素进行相似材料的选择和配比,并建立材料用量与力学指标之间的规律.文[7-8]将一元非线性回归分析分别应用于铁路隧道监控量测,以及软土隧道拱顶与地表沉降关系研究中.文[9]在对于公路隧道各类围岩稳定性的模型试验研究中,采用了重晶石粉、石英砂(中等粒径)和凡士林的热融混合材料作为不同围岩类别的相似材料.本文以贵广铁路各隧道开挖过程中需要穿越的Ⅳ,Ⅴ级围岩作为研究对象,对铁路隧道软弱围岩的相似材料进行试验研究及回归分析.
1 模型试验的理论基础
相似现象的同一物理量之比,称为相似系数,或称相似比例,用字母C表示.所有相似系数之间,存在着某种关系式,称为相似指标.与此对应,相似现象各物理量之间,也存在某种关系式,称为相似判据.
定义L为长度,γ为重度,E为弹性模量,σ为应力,ε为应变,c为凝聚力,φ为内摩擦角,μ为泊松比.文中所采用的记号和符号与文[10-12]同.根据原型和模型的平衡方程、几何方程、物理方程、应力边界条件和位移边界条件,可推导出如下3个地质力学模型试验的相似关系.
(1)应力相似系数Cσ、弹性模量相似比尺CE和应变相似比尺Cε之间的相似关系为

(2)地质力学模型试验要求所有无量纲物理量(如应变、内摩擦角、泊松比等)的相似比尺等于1,相同量纲物理量的相似比尺相等,即

由式(1),(2)可得

(3)应力相似比尺Cσ、容重相似比尺Cγ和几何相似系数CL之间的相似关系为

相似实验中,几何相似比和应力相似比均取为1∶30,由式(3),(4)可以推出需要进行测定的各弹性模量相似比亦为1∶30.
2 相似材料的选择
规范中规定的铁路隧道Ⅳ,Ⅴ级围岩的物理力学指标,如表1所示.在各个物理力学指标上,铁路隧道V级围岩与公路隧道的Ⅱ类围岩具有较强的相似性.
根据文[9]中对于公路隧道中各类围岩稳定性模型试验研究的成功经验,并经过若干次相似材料试制的基础上,最终采用重晶石粉、石英砂(中等粒径)和凡士林的热融混合材料作为铁路隧道Ⅳ,Ⅴ级围岩的相似材料.试验中,可以通过改变相似材料中各种组分的比例,达到在较大范围内调整相似材料的力学性能的目的,以满足相似指标的要求.

表1 围岩的物理力学指标Tab.1 Mechanical indexes of rock
常规三轴压缩试验一直是认识岩石在复杂环境(如地下水丰富和高地应力)下力学性质的主要手段,本试验在“应力控制式三轴试验仪”中进行.
试验全过程中围压保持为零,轴向压强的加载和卸载速率均为10 kPa·min-1.先加载3~5 min,使轴向压强达到试样峰值抗压强度的1/4左右后,再进行卸载直至轴向压强为零.为减小残余变形对试验结果的影响,将上述过程反复3次;然后,对试样加载直至其达到峰值抗压强度,并取最后一次加载过程开始阶段的应力-应变曲线直线段的斜率作为弹性模量的试验结果.
试验分为3组进行,在每一组试验中,将混合材料中的一种组分的含量作为变量,而将另外两种组分的含量取为常量进行试验.为了提高实验的精确度,对每个相同配方的混合材料重复试验3次,得到3个弹性模量,然后取其平均值作为试验的结果.不同含量热融混合材料组分的弹性模量,如图1所示.图1中:组分重晶石、石英砂、凡士林的混合占比分别用b,q,v表示.
3 试验过程与结果

图1 热融混合材料组分的弹性模量Fig.1 Elastic modulus of components of hotmeltmix material
4 试验结果的回归分析
对以上3个试验的结果进行一元线性(或非线性)回归分析[9],分别得到以下3个函数关系式.
4.1 凡士林含量与弹性模量的函数关系
设弹性模量为y,凡士林含量为x,从图1(a)中可以看到,散点并不接近某一条直线,呈现一个向上递增且下凸的趋势.经过统计软件SPSS进行回归拟合,可以得到回归曲线方程为

因此,可求得式(5)的剩余标准差为s1=9.27.
同理,还可以得到另外一个幂函数型的回归曲线方程为

因此,可求得式(6)的剩余标准差s2=13.97.由于s1 为了获取弹性模量为50.60 M Pa相似材料,根据式(5)选取混合比(b∶q∶v)为10∶4.5∶0.6的混合材料进行试验.将实测弹性模量值(y0)53.28 M Pa(图1(a)中的“o”点)与其相应的回归值(y^0)50. 60 M Pa进行比较,得到实测弹性模量的相对误差 由此可见,回归值与实测值相差不大,该混合材料的构造是可行的. 4.2 石英砂含量与弹性模量的函数关系 设弹性模量为y,石英砂含量为x.类似于凡士林含量与弹性模量的函数关系的求法,得到石英砂含量与弹性模量的函数关系式为 同样,为获取弹性模量为179.24 M Pa的相似材料,根据式(8)选取混合比(b∶q∶v)为10∶6.5∶1的混合材料进行试验.测得弹性模量值为172.61 M Pa(图1(b)的“o”点),相对误差e*q为3.84%. 4.3 重晶石含量与弹性模量的函数关系 设弹性模量为y,重晶石含量为x.从图1(c)可以发现8个点基本在一条直线附近,这说明两个变量之间存在线性关系.因此,用一元线性回归分析得到重晶石含量与弹性模量的函数关系式为 为了检验式(9)的合理性,考虑关于线性回归方程的显著性检验.方差分析的计算结果如表2所示.表2中:总平方和、残差平方和Se=∑(yi-y^i)2. 表2 方差分析表Tab.2 Analysisof variance 若取α=0.01,则F0.99(1,7)=12.25,由于1 197.19>12.25,因此,在显著性水平0.01下的线性回归方程式(9)是非常显著的.从图3也可以看出,其拟合程度是非常高的. 同样,为了获取弹性模量为268.55 M Pa的相似材料,根据式(9)选取混合比(b∶q∶v)为7∶4∶1的混合材料进行试验,可以测得弹性模量值270.27 M Pa(图1(c)的“o”点)及相对误差e*b为0.64%. 通过试验与回归分析,可以得到以下3点结论:(1)凡士林含量与弹性模量服从指数函数的函数关系,拟合程度较强.随着凡士林含量的增加,其弹性模量及弹性模量的增速均呈上升趋势;(2)石英砂含量与弹性模量服从对数函数的函数关系,拟合程度一般.随着石英砂含量的增加,其弹性模量呈上升趋势,但弹性模量的增速呈下降趋势;(3)重晶石含量与弹性模量服从线性函数的函数关系,且两者的相关性极强.随着重晶石含量的增加,其弹性模量呈下降趋势,且弹性模量的增速为常量. 综上所述,采用回归方程式(5),(8),(9),均可在一定范围内构造符合一定弹性模量的相似材料.鉴于在前面的分析中,相似材料的3种主要成分中仅重晶石含量与弹性模量有极强的线性关系,且在3组试验的回代所得的相对误差的比较中,不难发现采用回归方程式(9)所构造的相似材料的弹性模量的实测值与理论值的相对误差最小. 在实践中,可以适当选取石英砂和凡士林的含量作为常量,而取重晶石含量作为变量.经试验可求得重晶石与弹性模量回归方程式;同样,又可通过回归方程式来构造符合一定弹性模量的相似材料. [1] 陈荣淋,曾志兴.地下工程围岩稳定性评价的熵权系数法[J].华侨大学学报:自然科学版,2008,29(3):443-446. [2] 张强勇,李树才,郭小红,等.铁晶砂胶结新型岩土相似材料的研制及其应用[J].岩土力学,2008,29(8):2126-2130. [3] KIM S H,BURD H J.Model testing of closely spaced tunnels in clay[J].Geotechnique,1998,48(3):375-388. [4] SHAHAN IA R.Some p roblems in the antip lane shear defo rmation of bi-material wedges[J].International Journal of Solids and Structures,2005,42(11/12):3093-3113. [5] 刁心宏,刘士雨,官伟.软岩隧道围岩压力模型试验研究[J].华东交通大学学报,2008,25(5):1-7. [6] 范鹤,刘斌,王成,等.高填土涵洞相似材料的试验研究[J].东北大学学报:自然科学版,2007,298(8):1194-1197. [7] 王军保,张乔,包太.一元非线性回归分析在隧道监控中的应用[J].贵州工业大学学报:自然科学版,2007,36(6): 63-66. [8] 黄俊,张顶立.软土隧道拱顶与地表沉降关系研究[J].北京交通大学学报:自然科学版,2005,29(1):36-40. [9] 肖林萍,赵玉光,申玉生.双连拱隧道结构内力样式及围岩稳定性模型试验研究[J].岩石力学与工程学报,2005,24 (23):4346-4351. [10] 茆诗松,丁元,周纪乡,等.回归分析及其试验设计[M].上海:华东师范大学出版社,1984. [11] 李忠献.工程结构实验理论与技术[M].天津:天津大学出版社,2004. [12] 张强勇,李树才,焦玉勇.岩体数值分析方法与地质力学模型试验原理及工程应用[M].北京:中国水利水电出版社,2005. [13] 郭富利,张顶立,苏洁,等.地下水和围压对软岩力学性质影响的试验研究[J].岩石力学与工程学报,2007,26 (11):2324-2332. Mechan ical Properties of Sim ilar Materials for Soft Rock in Tunnel WANG Shu,ZHANG Ding-li,FANG Qian Based on similarity theo ry and dimensional analysis,adop ting elastic modulus as the research index of soft rock in railway tunnel,a similarity index is deduced.Taking the mixture of barites,quartz sand and Vaseline as similar materials fo r soft rock,a similarity simulation test is conducted through conventional stress-controlled triaxial apparatus. Analyzing the experimental results by themethod of non-linear regression,the mixture ratio of similar materials and the variation of elastic modulus are obtained.The function to estimate the relationship between elastic modulus and the content of essential component of similar material such as barites is got,w hich can be used to make the app rop riate similar material in model experiment of tunnel soft rock. soft rock;elastic modulus;similarity theo ry;Similar material;nonlinear regression U 452.1+2 A (责任编辑:黄仲一 英文审校:方德平) 1000-5013(2010)06-0680-04 2010-06-23 张顶立(1963-),男,教授,博士生导师,主要从事隧道及地下工程的研究.E-mail:zhang-dingli@263.net. 国家重点基础研究发展计划(973)项目(2010CB732100);铁道部科技研究开发计划重大项目(2009G005)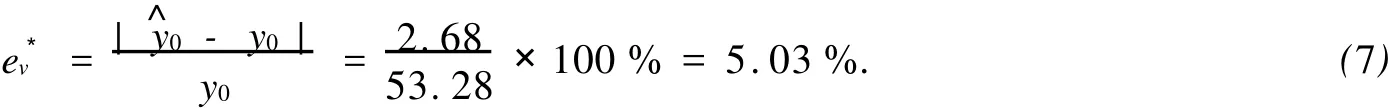



5 结论
(Tunnel and Underground Engineering Research Center of Ministry of Education,Beijing Jiaotong University,Beijing 100044,China)

