基于热传导模型的像素级遥感图像融合

许君一,卢秀山,卿熙宏,姚继锋

1.山东科技大学测绘科学与工程学院,山东青岛266510;2.山东省3S工程技术研究中心,山东青岛266510;3.海岛(礁)测绘技术国家测绘局重点试验室,山东青岛266510;4.山东科技大学资产处,山东青岛266510

基于热传导模型的像素级遥感图像融合

许君一1,2,3,卢秀山1,3,卿熙宏1,4,姚继锋1

1.山东科技大学测绘科学与工程学院,山东青岛266510;2.山东省3S工程技术研究中心,山东青岛266510;3.海岛(礁)测绘技术国家测绘局重点试验室,山东青岛266510;4.山东科技大学资产处,山东青岛266510

通过热传导方程给出一种像素级遥感图像融合模型和方法:①给出空间域内高分辨率图像与低分辨率图像之间的扩散关系,作为特例得到Brovey变换(brovey transform,BT);②给出图像融合与增强的统一表达式并得到基于亮度平衡的融合方法;③低分辨率多光谱图像的方差较小情形,指出基于方差的标准图像融合方法将会丢失高空间分辨率全色图像信息。试验表明,除了图像量化误差以外,所提议的方法不会丢失已知图像的空间分辨率和波谱信息。

图像融合;遥感;HSI;多光谱图像;热传导方程

1 引 言

遥感图像处理中,高空间分辨率全色图像与低空间分辨率多光谱图像的融合技术一直是其研究重点之一。像素级融合方法大体上可分为颜色模型法(HSI、HSB、HSV等)、变换域法(离散小波变换DWT、主分量法 PCA等)、参数估计法[1]。颜色模型法中,HSI变换因其亮度空间与彩色空间的正交性而受到重视。参数估计法中, Bayes法也有比较满意的结果[2]。文献[2]通过引入多个观测模型,增强了待估计图像各个主成分的空间分辨率,并获得了线性最小均方误差意义上的高分辨率多光谱图像Bayes估计。变换域融合方法中最常见的DWT法以适当损失空间分辨率为代价较好地保留了波谱信息[3-4]。也有作者通过DCT变换进行图像融合[5]。有一些作者从波谱保持性角度研究多光谱遥感图像融合问题[6]。从应用角度分析,各种图像融合方法各具特点[7]。方法研究方面,人们不断探索新的图像融合方法使其更具有普遍性和更好的效果。如,偏微分方程理论正逐渐受到重视[8-9]。

现代图像处理中,非线性扩散方程在图像的复原、边缘检测、分割及去噪等问题中有着重要的应用[7-9]。自从1987年Malik和 Perona把非线性传播(扩散)方程引入到图像处理后,人们大量研究了具有对比度不变性、仿射不变性的非线性扩散方程[7-8]。D.A.Socolinsky在他的博士论文中通过偏微分方程研究了图像融合问题[10]。D.A.Socolinsky的研究为图像融合问题提供了新的思路和方法[11-12]。

热传导方程在研究许多扩散问题时起到借鉴作用。用热传导方程来描述图像的多尺度空间分辨率和图像的复原问题已经有丰富的成果[6-7]。笔者通过扩散原理和偏微分方程理论研究了低空间分辨率多光谱波段图像与高空间分辨率全色波段图像的融合问题。试验表明,新方法的理论结果是稳定和正确的。

2 基于扩散模型的多光谱和全色波段图像融合

热扩散过程与图像的多尺度分辨率之间有许多相似或相同之处。下面通过热扩散原理建立多光谱和全色波段图像融合的热传导模型及算法。

2.1 热传导扩散模型

设高空间分辨率多光谱图像在0≤t≤T内发生扩散且满足热传导方程。多光谱图像的多尺度热传导方程与一般热传导方程约束条件有所不同的是,模型中增加了终止条件。为了融合后的图像亮度与多光谱图像亮度保持一致,给出了均值约束条件。作为可选项,给出了表示图像细节反差的方差约束作为候选条件。根据以上假设,多尺度图像热传导方程模型为

其中,k=1,2,3,4分别代表R、G、B三个波段及图像亮度;φ(x)表示高空间分辨率全色图像。作为扩散条件,初始图像φk(x)表示高分辨率图像(若无特别声明以下分辨率均指空间分辨率);终止图像ψk(x)表示低分辨率图像;uk(x,t)为 t尺度图像;E(＊)表示图像平均值;D(＊)表示图像方差。假定ψk(x)是φk(x)经过 T时间尺度扩散的结果。所以,φk(x)的分辨率高于ψk(x)。对于多光谱k=1,2,3情况,式(1)构成求解初始条件φk(x)和热源函数 fk(x,t)的反问题。理论上,式(1)的求解是困难的。

图像亮度一般是各个波段灰度的平均值

所以,多光谱图像亮度 u4(x,t)在也满足式(1)的形式。式(1)的Fourier变换为(ξ=(ξ1,ξ2,ξ3)T)

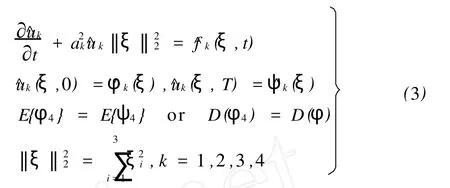
求解式(3)得(k=1,2,3,4)

式(3)中要求满足条件^uk(ξ,T)=^ψk(ξ),即

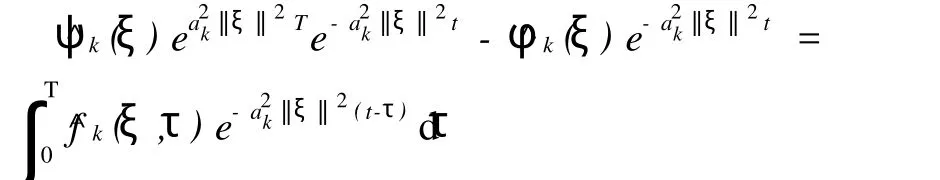
令χ(τ)为特征函数

则

做关于t的Fourier变换得

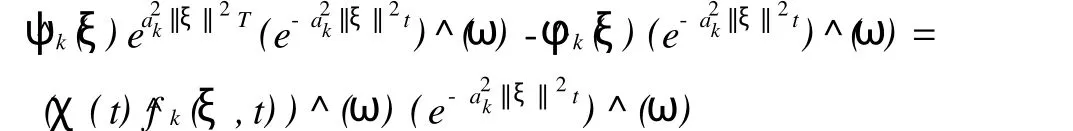
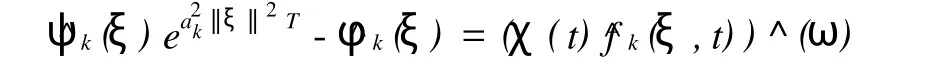
即做逆Fourier变换并求函数^fk(ξ,t)得

其中,δ(t)为Dirac函数,t∈[0,T]。把上式代入下式

得

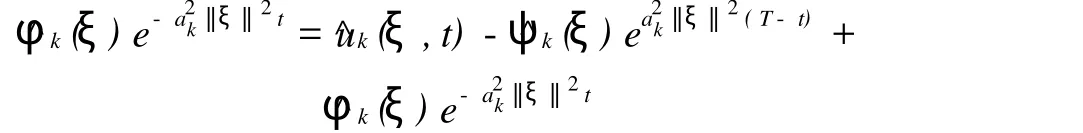
整理和考虑t=0情况,得

2.2 多光谱与全色波段图像融合

根据式(4),有

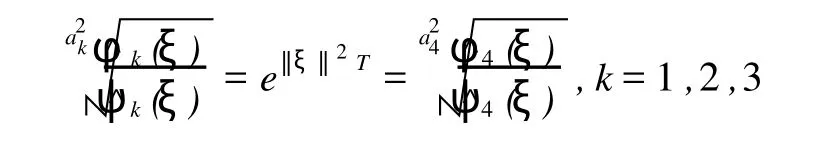
即

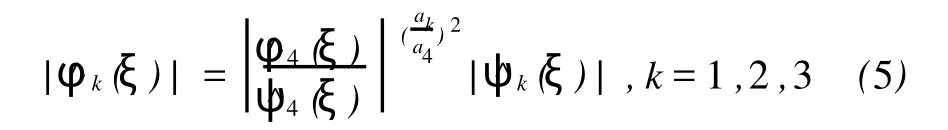
复数模|＊|代表了图像的能量。如果把像素值作为该点的能量,复数模|＊|代表了构成该像素的更小尺度图像的能量。如图1所示,数字图像的获得可看成如下过程:大图像是由子图像拼接得到的。

图1 大图像由子图像拼接得到Fig.1 Sub-image to be large mosaic image

把子图像缩减成一个光栅点构成新的数字图像

根据式(6),式(5)表示低分辨率多光谱子图像、高分辨率全色子图像及高分辨率多光谱子图像之间的能量关系。这种能量关系,对大的图像来说就是像素值之间的关系。通过式(5)、式(6),从子图像频率域转换到大图像空间域

根据式(7),可通过全色图像φ4和低分辨率多光谱图像获得高分辨率的多光谱图像(φ1,φ2,φ3)。理想情况下,高分辨率多光谱图像的亮度φ4和高分辨率全色图像φ完全一致。但从信息获取角度看,φ和φ4的区别是φ为已知量,φ4为未知量。用已知的φ代替未知的φ4得到

若假定 ak=a(k=1,2,3),t∈[0,T],根据式(2),自然有 a4=a。此时直接得到 Brovey变换(Brovey transform,BT)[13]。在热扩散过程中其总能量守恒。所以,扩散过程中可以认定多光谱图像的各个波段平均亮度不变,E{ψk}=E{φk}(k =1,2,3)。但是,遥感图像中常见情况是低分辨率的多光谱图像的亮度与全色图像的亮度不一致。因此,对式(8)进行如下调整

其中,k=1,2,3。式(11)将使得到的高分辨率多光谱图像与低分辨率多光谱图像的亮度保持一致。当ak=a(k=1,2,3),t∈[0,T]时,由式(9)进一步得

经过式(10)给出的高分辨率多光谱图像的亮度方差为(用D(＊)表示方差)

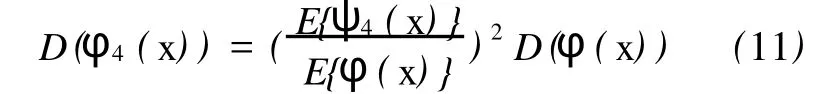
同理,通过式(8)也能得到常用的标准图像融合算法

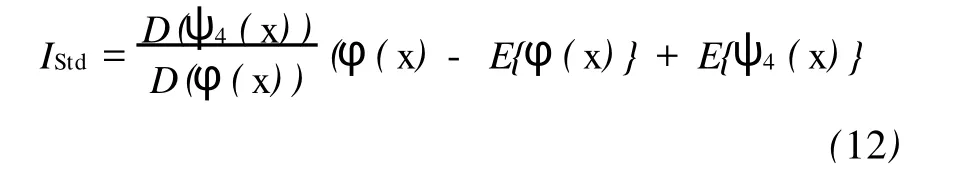
值得注意的是,式(12)的方差 D(IStd)=D(ψ4)而不是D(IStd)=D(φ)。所以,式(12)的分辨率不能很好地代表高分辨率图像的分辨率。另外,当D(ψ4)≈0时出现 D(IStd)≈0,即得到亮度为E{ψ4(x)}的无图像细节的同一色图像。这与事实是不符合的。实际上,多光谱图像方差为0未必全色图像没有细节。在数字图像中均值为0的图像方差一定为0,但反过来未必成立。从这个角度,式(7)～式(9)和式(9)～式(10)更具有普遍意义。从实际应用角度,式(12)也不是完全不可用。当低分辨率光谱图像亮度方差D(ψ4)比较大时,式(12)的效果不仅很好而且表现出对波谱信息的高分辨率特性。所以,更为实际的方案是要依据所获得的图像和应用要求决定采用哪一个。

3 试验与分析

以下试验原始影像均为256×256的低分辨率多光谱图像和高分辨率全色图像。试验中,除了特别指出参数

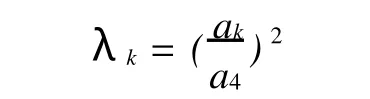
以外,都默认为λk=1(k=1,2,3)。称参数λk为反扩散系数。

试验1 图2为原始影像。图3(a)、(b)通过式(8)、式(9)得到。目视效果上,图3(a)亮度与图2(b)一致,图3(b)亮度与图2(a)一致。这一点同理论分析一致。图4通过式(12)得到。细节反差上,图4不如图3(b)。图4整体亮度相对较低,在高亮度区可分辨部分细节。

图2 低分辨率多光谱图像(a)和高分辨率全色图像(b)Fig.2 The low-resolution multispectral images(a)and the high-resolution panchromatic image(b)

图3 (a)、(b)分别为通过式(8)和式(9)得的结果Fig.3 (a)and(b)are obtained by method(8)and (9),respectively

图4 根据式(12)得的结果Fig.4 The result obtained by method(12)

图5 原图像Fig.5 The original image

试验2 图5、图6为原始影像。图5为高分辨率多光谱图像。图7(a)直接通过式(9)得到,图7(b)通过亮度与彩色空间正交的HSI变换后,对亮度分量用式(12)处理,然后进行HSI反变换得到。表1为均方误差

其中,(si,j)为原始高分辨率多光谱图像,(f usioni,j)为融合后的图像。图8(a)、(b)通过式(9)得到。其中反扩散系数λk=0.2,1.8(k=1,2,3)。

图6 低分辨率多光谱图像和高分辨率全色图像Fig.6 The low-resolution multispectral images(a)and the high-resolution panchromatic image(b)

图7 (a)、(b)分别为通过式(9)和式(12)得的结果Fig.7 (a)and(b)are obtained by method(9)and (12),respectively

图8 (a)、(b)经式(9)得到,λk=0.2,1.8(k=1,2,3)Fig.8 (a)and(b)are obtained by method(9)using parametersλk=0.2,1.8(k=1,2,3),respectively

试验3 原始影像如图9所示。图10(a), (b)通过式(10),式(12)得到。图10(b)没有能够体现出高分辨率全色图像的信息。这与理论分析一致。

图9 低分辨率多光谱图像和高分辨率全色图像Fig.9 The low-resolution multispectral images(a)and the high-resolution panchromatic image(b)

图10 (a)、(b)分别为通过式(9)和式(12)得到的结果Fig.10 (a)and(b)are obtained by method(9)and (12),respectively

表1 试验2的RGB波段均方误差Tab.1 Themeansquared errorofRGB bandin second experiment

试验4 采用试验1的图像数据进行基于4层小波分解的两种融合算法试验。

融合方法1 ①对图2(a)进行HSI变换,获得亮度分量I;②对I和图2(b)进行4层小波分解,小波采用db4(daubechies 4);③在第4层,低频取I的低频分量,高频取I和图2(b)相互对应的高频分量中系数绝对值大的作为新的高频分量,并把这些高低频分量作为图2(b)的第4层小波分解分量;④对图2(b)进行逐层小波重构,其结果作为新多光谱图像的HSI亮度分量I;⑤进行HSI反变换,得到图11(a)。

融合方法2 ①进行融合方法1中的过程①和②;②在第4层,通过I和图2(b)的第4层低通分量进行主成分分析(PCA)得到权值;③对I和图2(b)的第4层分量进行加权求和,并把它作为图2(b)的第4层分量;④对图2(b)进行逐层小波重构和HSI反变换,得到图11(b)。试验中,对应全色和多光谱图像的权值分别为0.376 72和0.623 28。

图11 图像(a)是试验4融合方法1的结果,而图像(b)是融合方法2的结果Fig.11 (a)and(b)are the results of fusion method 1 and 2 in experiment 4,respectively

分析 试验1中,整体上亮度约束效果比方差好。在高亮度区域,由于低分辨率多光谱图像高亮度区的过高亮度和融合图像的量化截断,导致图3(b)在高亮度区域难于分辨空间细节。基于方差的融合图像图4在高亮度区体现了一定的细节。试验2给出了融合图像和原始图像的差别程度。目视效果图7(a)比图7(b)好一些,但差别不明显。表1数据表明,各波段的平均离散程度都很小。由式(9)和式(10)得到图像的均方误差完全一样。这也从另一个方面说明了亮度空间与彩色空间正交的 HSI变换的合理性。图8(a)、(b)表明,融合中扩散条件的不同而表现出图像的逐渐增强。不同的参数代表了不同的扩散程度,所以当加大逆扩散程度时表现出了使图像增强的特点。试验1～试验3表明了理论与试验的一致性,同时指出了用亮度作为约束条件比用方差作为约束条件更有效和合理。试验3直接指出了方差约束在极端情形下的不合理性。试验4给出了两种典型的小波融合试验。目视效果上,图11(a)的波谱信息与图2(a)比较接近。在细节上和清晰程度上,图3(b)的空间分辨率明显好于图11(a)。虽然图11(b)在细节保持性上有一定的改进,但较多地丢失了波谱信息。所以,无论是波谱信息保持性上还是空间分辨率上,图11(b)都不如图3(b)。目前,小波融合算法的多数融合策略是取多光谱的低频和全色波段的高频作为融合策略,其目的是保持多光谱的波谱信息和全色波段的高空间分辨率信息。研究表明,小波融合算法中的分解层数不是越多或越少就越好。因此,许多小波图像融合算法对空间分辨率和波谱信息损失是不可避免的。如何使空间分辨率和波谱信息的损失减少到最少是小波图像融合技术中的一个核心问题。试验4的结果也说明了这个问题。在空间分辨率和波谱信息损失中,不仅有目视效果上可感觉得到的损失,也有感觉不到的损失。这些损失是小波分解下的图像融合策略导致的。这一点上,新方法具有空间分辨率和波谱信息保持性上的优势。

4 结 论

笔者根据热传导方程得到了图像融合算法。根据热传导方程,理论上得到了BT算法和融合与增强统一描述的更一般的算法。试验表明,该算法在波谱保持性和细节保持性上表现出比较好的特性。分析和试验表明,标准图像融合算法在方差比较小时丢失高分辨率全色图像信息。从多光谱波谱信息上,除了调整波谱亮度以外,新方法在不同波谱之间的相对比值关系没有发生变化。所以,从波谱之间的比值角度来说,融合结果没有发生波谱畸变。新方法适合应用于遥感图像目视解译与分析。新方法不需要做 HSI变换,这将有效减少计算量。相对于Bayes法,新方法无需进行迭代计算,也没有像Bayes法中出现的光谱信息和空间细节信息等方面的预测或估计问题。新方法是基于热扩散理论的方法,理论上是严格而精确的算法,无须进行最优性估计。融合原理试验结果表明,新方法在细节保持性上优于多层小波分解方法。

新算法精度在于,不同分辨率的遥感图像融合是否符合扩散原理。作为新方法特例的BT方法文献和本文试验表明,多尺度意义上的扩散模型满足热传导方程在内的扩散方程。所以,新方法不仅具有一定的普适性,更具有进一步进行理论发掘的潜力。多光谱融合图像的波谱真伪与低分辨率的多光谱图像的扩散程度有直接关系。如果扩散程度过大,其光谱不能代表高分辨率空间位置的波谱信息。因此,在适当的波谱空间分辨率下的融合才有实际意义。

根据以上分析和结论,所提议的方法具有较强的理论意义和较好的实际意义。根据本文研究结果和思路,将进一步研究多焦距图像融合的扩散模型和非线性融合模型。

[1] ZHANG Yujin.Image Engineering[M].2nd ed.Beijing: Tsinghua University Press,2007:315-343.(章毓晋.图像工程[M].2版.北京:清华大学出版社,2007:315-343.)

[2] GE Zhirong,WANG Bin,ZHANG Liming.Remote Sensing Image Fusion Based on Bayesian Linear Estimation [J].Science in China:Series F,Information Sciences, 2007,50(2):227-240.(葛志荣,王斌,张立明.基于Bayes线性估计的遥感图像融合[J].中国科学:F辑,信息科学,2007,37(4):501-513.)

[3] LIU Bin,PENGJiaxiong.Fusion Method of Multi-spectral Image and Panchromatic Image Based on Four Channels Non-separable Additive Wavelets[J].Chinese Journal of Computers,2009,32(2):350-356.(刘斌,彭嘉雄.基于四通道不可分加性小波的多光谱图像融合[J].计算机学报,2009,32(2):350-356.)

[4] LIANG Dong,LI Yao,SHEN Min,et al.An Algorithm for Multi-focus Image Fusion Using WaveletBased Contourlet Transform[J].Acta Electronica Sinica,2007, 35(2):320-322.(梁栋,李瑶,沈敏,等.一种基于小波-Contourlet变换的多聚焦图像融合算法[J].电子学报, 2007,35(2):320-322.)

[5] CHU Heng,WANG Ruyan,ZHU Weile.Remote Sensing Image Fusion Algorithm in the DCT Domain[J].Acta Geodaetica et Cartographica Sinica,2008,37(1):70-76.(楚恒,王汝言,朱维乐.DCT域遥感影像融合算法[J].测绘学报,2008,37(1):70-76.)

[6] WU Lianxi,LIANG Bo,LIU Xiaomei,et al.A Spectral Preservation Fusion Technique for Remote Sensing Images [J].Acta Geodaetica et Cartographica Sinica,2005,34 (2):118-128.(吴连喜,梁波,刘晓梅,等.保持光谱信息的遥感图像融合方法研究[J].测绘学报,2005,34(2): 118-128.)

[7] CHENG Yinglei,ZHAO Rongchun,LI Weihua.et al. Overview of Methods of Data Fusion for Images Based on Pixel-level[J].Application Research of Computers,2004, 4(5):169-172.(程英蕾,赵荣椿,李卫华,等.基于像素级的图像融合方法研究[J].计算机应用研究,2004,4 (5):169-172.)

[8] SAPIRO G.Geometric Partial Differential Equations and Image Analysis[M].Cambridge:Cambridge University Press,2001:260-340.

[9] MAITRE H.Le Traitement des Images[M].Translated by SUN Hong.Beijing:Publishing House of Electronics Industry,2006:156-173.(MAITRE H.现代数字图像处理[M].孙红,译.北京:电子工业出版社,2006: 156-173.)

[10] SOCOLINSKY D A.A Variational Aproach to Image Fusion[D].Baltimore:Johns Hopkins University,2000.

[11] SOCOLINSKY D A.Dynamic Range Constraints in Image Fusion and Visualization[C]∥Proceedings of Signal and Image Processing 2000.Las Vegas:[s.n.],2000: 349-354.

[12] SOCOLINSKY D A,WOLFF L B.A New Visualization Paradigm for Multispectral Imagery and Data Fusion[C]∥Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition:Vol 1.Fort Collins:IEEE,1999:319-324.

[13] POHL C.Tools and Methods for Fusion of Images of Different Spatial Resolution[C]∥International Archives ofPhotogrammetry and Remote Sensing:Vol32. Valladolid:[s.n.],1999:76-82.

(责任编辑:丛树平)

Pixel-level Remote Sensing Images Fusion Based on Heat Conduction Model

XU J unyi1,2,3,LU Xiushan1,3,QING Xihong3,YAO Jifeng1
1.College of Geomatics,Shandong University of Science and Technology,Qingdao 266510,China;2.“3S”Research Center of Engineering and Technology,Qingdao 266510,China;3.KeyLaboratory of Surveying and Mapping Technology on Island and Reef, State Bureau of Surveying and Mapping,Qingdao 266510,China;4.Assets Division,Shandong University of Science and Technology, Qingdao 266510,China

A novel pixel-level remote sensing image fusion based on heat conduction equation is proposed.The main contributions are as follows:①the diffusion relationship between the high-resolution image and the low-resolution image are obtained in the space domain,where Brovey transform(BT)is one of its special cases;②a unified expression of pixel-level image fusion and image enhancement is obtained,and a brightness balanced-based image fusion is obtained by using the expression;③the disadvantage that the standard variance-based image fusion method will result in the loss of high spatial resolution panchromatic image information,for smaller variance of lowresolution multispectral images is pointed out.Experimental results show that this approach does not lose the image spatial resolution and spectral information and outperforms the existing method.

image fusion;remote sensing;HSI;multispectral image;heat conduction equation

XU J unyi(1960—),male,PhD,professor,majors in the image processing,pattern recognition,digital watermarking,digital photogrametry and marine charting.

E-mail:xjyxxl@yahoo.com.cn

1001-1595(2010)06-0566-06

P237

A

国家自然科学基金(30700107)

2009-08-01

2009-09-28

许君一(1960—),男,博士,教授,主要研究方向为图像处理、模式识别、数字水印、数字摄影测量和海洋测绘。