曲线系方程的应用反思与课堂生成资源的利用*

方雷

(楚雄第一中学，云南 楚雄 675000)

曲线系方程的应用反思与课堂生成资源的利用*

方雷

(楚雄第一中学，云南 楚雄 675000)

在课堂教学中，抓住课堂生成资源，引导学生自主探究，让学生从提出问题到探索结论的过程中，获得自主学习的体验和成功的快乐，从而激发学生学习兴趣，培养学生的探究意识和创新精神。经验型和专家型的教师更要重新审视自己已经熟悉甚至麻木的教学内容，对可能产生课堂生成资源的内容做必要的引导和启发，并对已经产生或者可能产生的课堂生成资源，提出了教师应有的知识准备和策略预设。

教学反思;自主探究;课堂生成资源;策略预设

0.引言

人教版高中数学(必修)第二册(上)复习参考题七B组第四题有以下结论:两条曲线的方程是C1:f1(x，y)=0和C2:f2(x，y)=0，它们的交点是P(x0，y0)，求证方程f1(x，y)+λf2(x，y)=0的曲线C也经过点P(λ是任意实数)。

以上结论在很多教辅资料中都有收录，并被广泛应用于解决直线系和圆系的问题。在教学中，我也会在适当的时候介绍该结论，并引导学生应用该结论解决相关问题，但多年来也仅仅停留在模仿应用的层面，未作深入的研究。

1.正文

2009年12月7日，在我所教的理科实验班的一节复习课上，我复习了这一结论。在对结论进行简单证明之后，一名学生提出了以下问题:“已知曲线C1:f1(x，y)=0和C2:f2(x，y)=0，当曲线C1和C2无公共点时，方程f(x，y)+λf2(x，y)=0(λ是任意实数)的曲线C与曲线C1、C2有何关系?”面对这一突如其来的问题，我意识到这是一个鼓励学生自主探究的极好切入点。于是，我先让学生凭直觉或经验猜测这一问题的结果。课堂经过短暂的沉默之后，有学生说:这样的方程不表示任何曲线;而有的则说如果该方程能表示一条曲线，则这条曲线和C1、C2都相交;也有人说如果该方程能表示一条曲线，则这条曲线和C1、C2都不相交。在这一过程中，我让学生充分发挥其想象力，不对他们的猜想进行评论，只对学生的猜测进行规范化的表达和复述。为了降低问题的难度，让学生对问题的理解更具体，在学生充分发表意见之后，我建议学生从C1:f1(x，y)=0和C2:f2(x，y)=0都表示圆或者都表示直线且λ=±1的特殊情况入手，先用特例进行探究检验，再从所拥有的教辅资料中查找相关的题目作为例证，并鼓励学生尽量从理论上对自己的结论进行论证。课下，我进行了思考，同时关注学生的探究过程，两天后，学生得出了以下一组结果或例证:

(1)对于直线C1:Ax+By+C1=0和C2:Ax+By+C2=0(C1≠C2)，则当λ≠－1时，方程Ax+By+C1+λ(Ax+By+C2)=0表示与C1、C2平行的直线，且该直线分C1、C2间的垂线段(有向线段)的比为λ;当λ=－1时，方程Ax+By+C1+λ(Ax+By+C2)=0不表示任何曲线。

(2)对于圆C1:x2+y2+D1x+E1y+F1=0和C2:x2+y2+D2x+E2y+F2=0(C1、C2无公共点)，则方程x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0不表示任何曲线或所表示的曲线与C1、C2也没有公共点。

例如:对于曲线C1:x2+y2－1=0与C2:x2+y2－4=0，当λ=1时，方程方程f1(x，y)，所表示的曲线与C1、C2都没有公共点;λ=－1时，方程f1(x，y)+λf2(x，y)=0不表示任何曲线(仅为学生所举例证，该结论不具备一般性)。

(3)对于圆C1:x2+y2+D1x+E1y+F1=0和C2:x2+y2+D2x+E2y+F2=0，当C1、C2相切时，则方程x2+y2+D1x+E1y+F1－(x2+y2+D2x+E2y+F2)=0表示过切点的公切线。

例如C1:x2+(y－4)2－36=0与C2:(x－3)2+y2－1=0，当λ=－1时，方程f(x，y) +λf2(x，y)=0化为3x－4y－14=0，该方程表示过C1、C2切点的公切线。

(4)已知C1:f1(x，y)=0和C2:f2(x，y)=0，当曲线C1和C2无公共点时，方程f1(x，y)+ λf2(x，y)=0(λ是任意实数)如果能表示某一曲线，则该曲线与曲线C1、C2都没有公共点。

例如:(2005江苏)如下图，⊙O1和⊙O2的半径都等于1，|O1O2|=4，过动点P作⊙O1和⊙O2的切线PM、 PN(M、N为切点)，使得，试建立平面直角坐标系，，并求动点P的轨迹轨迹方程。

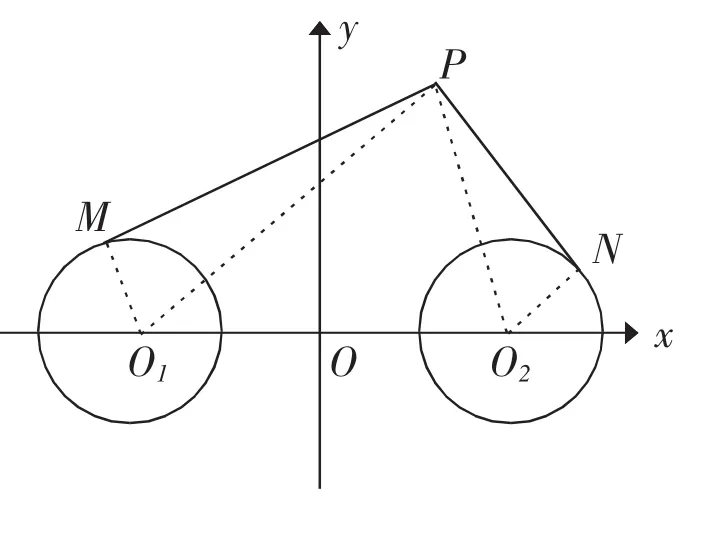
略解:建立如图所示直角坐标系，设P(x，y)，

则(x+2)2+y2－1=2［(x－2)2+y2－1］，化简得(x－6)2+y2=33就是所求的轨迹方程。

以上解答中的(x+2)2+y2－1=2［(x－2)2+y2－1］，即相当于问题中λ=－2的情形。曲线(x－6)2+y2=33与⊙O1、⊙O2都没有公共点。

一般地，若C1:f1(x，y)=0和C2:f2(x，y)=0无公共点，则方程组无解，所以都无解，结论4得证。

这次教学中的“意外”，使我对多年来感觉熟悉而从不质疑的内容，产生了一些批判性的思考;对学生的探究和创新能力，有了进一步的认识;对如何激发和利用课堂生成资源，培养学生的探究意识和学习兴趣等教学方法及策略，有了新的感悟。吸取以上教训，在基本完成“椭圆的几何性质”教学内容之后，我对所教的理科实验班给出了以下问题，为学生进行探究埋下伏笔。

已知直线l:y=2x+3与坐标轴相交于A、B两点，动点Q在线段AB上移动，求点Q到椭的右焦点和右准线的距离之比的最小值。

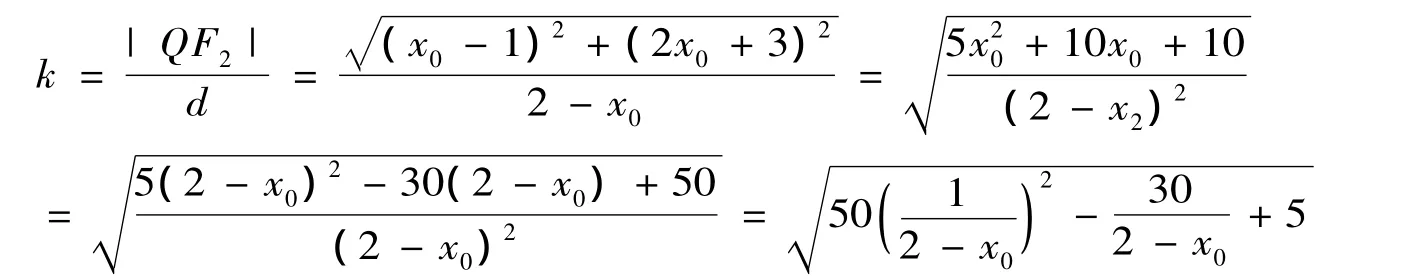
大多数学生都能在课后完成以上解答，而且让我欣慰的是，有学生验证了点是直线l与椭圆C的切点，发现了线段AB上其它的点都在椭圆的外部，并结合椭圆的第二定义，提出了以下猜想:椭圆上的点到焦点和对应准线的距离之比等于离心率;椭圆外的点到焦点和对应准线的距离之比大于离心率;椭圆内的点到焦点和对应准线的距离之比小于离心率。此时，我对学生的猜想给出了充分的肯定，并鼓励学生自己判断猜想的真假。第二天，学生就给了我以下的证明:

设点Q(x0，y0)是椭圆

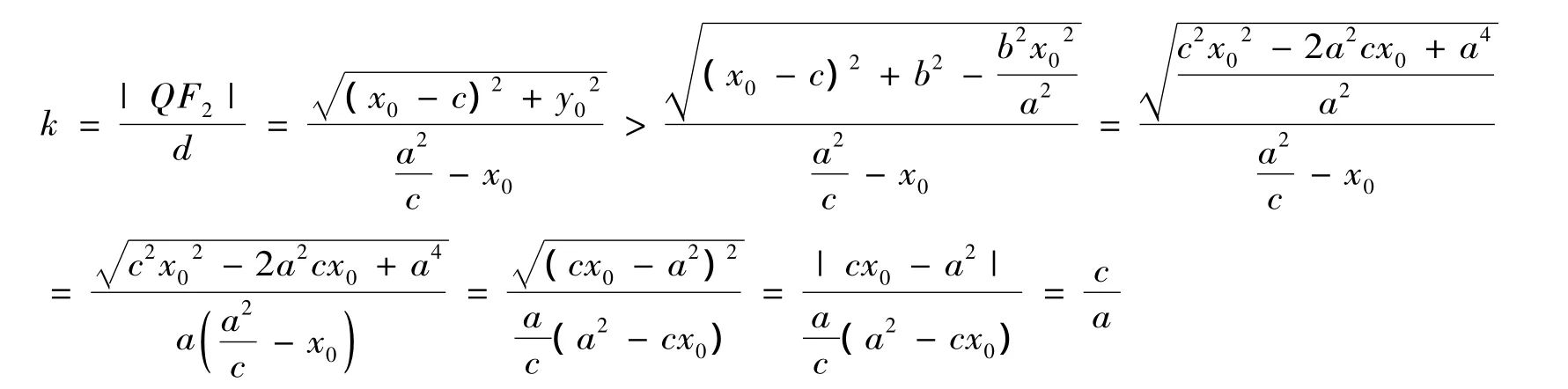
有了以上两次学习经历，部分学生的创新意识和探究精神有了一定的提高，在完成了双曲线和抛物线的学习后，多数学生又针对双曲线和抛物线，重新研究了以上问题;而且对以下问题:“过抛物线y2=px(p＞0)的焦点，作直线与抛物线交于A、B两点，求证，以AB为直径的圆与抛物线的准线相切。”学生在解决该问题之后，有更多学生自然的就提出了“对于椭圆和双曲线，是否有类似的结论?”这样的问题，也有学生提出了以下问题:“已知直线l过点M(m，0)，与抛物线y2=2px(p＞0)交于A、B两点，当0时，判断以AB为直径的圆与抛物线的准线的位置关系。”在我的鼓励和指导下，提出这些问题的学生最终都自主解决了这些问题。

上述由学生提出的系列问题，的确显得稚嫩，学生对有些结论也还不能完成严密的论证，但他们从提出问题到探索结论的过程中，获得了自主学习的体验和成功的快乐。对激发学生学习兴趣以及培养学生的探究意识和创新精神有很大的促进作用。

2.结论

通过对以上几次教学过程的反思，我认为，经验型和专家型的教师更要重新审视自己已经熟悉甚至麻木的教学内容，对可能产生课堂生成资源的内容做必要的引导和启发，并对已经产生或者可能产生的课堂生成资源，教师要有以下的知识准备和策略预设:

(1)有坚实的专业功底。面对学生可能产生的各种“稀奇古怪”的问题，教师要能从专业的角度及从理论的高度进行探究，成为学生创新思维和研究性学习的参与者、引领者和评价者。

(2)有承认“我不会”的气度。学生的思维火花，总会照到老师的认知盲区，面对突发状态，教师不能用“这个问题太难，不适合你”或“这种问题太偏，没有什么实际意义;高考从来不考，不用管它”之类的话来敷衍学生，而是要有承认我不会的气度，引导及参与学生的主动探索和研究，激发和保护学生的探究意识和创新精神。这样，才能更好的把握住教学的契机，化被动为主动，增强教学效果，提升教师的人格魅力。

(3)必要时有“我不会”的糊涂。对一个功底扎实的教师来说，学生的大多数问题，都是教师能完全掌控和把握的问题，此时教师要是每问必答，固然能树立教师的良好形象，但也可能让学生对教师产生高山仰止不可超越的心态，使学生失去主动探索的机会和发现的快乐，久而久之，也不利于学生探究意识和创新精神的培养。所以，对于一些适合学生自主学习的问题，教师即使成竹在胸，也可以有“我不会”的糊涂，给学生留出探究的空间。

(4)鼓励学生“反弹琵琶”。教师经常会有这样的困扰:对于某类问题，老师已经给出了最简解法，但学生却经常别出心裁，对老师推荐的方法置若罔闻，自己搞出一个舍近求远费时费力的解法，面对这样的情况，教师不应该有白费力气的愤慨，更不应该责怪学生“离经叛道”，而是要为学生的行为感到高兴，学生的解法虽然不是最优解法，但对他来说，却是一个自主创新的过程。所以，教师要允许甚至鼓励学生怀疑结论、反叛经典。这往往是学生创新意识的萌芽和自主探究的开始。

(责任编辑 刘洪基)

Reflection for the Curvilinear Equation Application and Utilization of the Classroom Generic Resources

FANG Lei
(Chuxiong First Middle School of Yunnan Province，Chuxiong 675000，China)

Based on the reflection of teaching process，the author hold that the teachers must re－examine their numbing teaching contents.Teachers must give necessary guidance and inspiration to students on the potential classroom generic resources contents.The author puts forward the knowledge preparation and strategy preferences to point against produced or may generation classroom resources.

teaching reflection;experience task;classroom generic resources;strategy preferences

G633.6

A

1671－7406(2010)06－0105－04

2010－04－17

方 雷 (1966—)，男，云南南华县人，中学高级教师，主要从事中学数学教学与研究。