朱昌河特大桥桥墩边坡稳定性分析与治理

徐宗苏,吴凯峰,隆 然

(中交第二公路勘察设计研究院有限公司,湖北武汉 430056)

朱昌河特大桥桥墩边坡稳定性分析与治理

徐宗苏,吴凯峰,隆 然

(中交第二公路勘察设计研究院有限公司,湖北武汉 430056)

岩质边坡问题是中国20世纪80年代以来出现的最具特色的工程地质问题之一。由于岩质边坡是一个非线性的、不确定的动态系统,边坡稳定性分析与评价较为复杂,需要对其不断地进行深入研究。以朱昌河特大桥4号桥墩所在边坡为例,利用极限平衡法和有限元法计算,模拟边坡的稳定性,根据计算、模拟结果采用预应力锚索、锚杆进行了边坡加固,为今后同类边坡的稳定性分析提供了有益参考。

边坡稳定性;极限平衡法;有限元法

0 引言

高边坡是一个复杂的、受多因素影响的动态系统,具有非线性和不确定性特征[1]。边坡稳定性分析与安全评价是边坡工程研究的重要核心内容,贯穿于边坡工程发展研究的始终。由于稳定性评价方法的不确定性,使得边坡稳定性评价成为一个相当复杂的问题[2]。虽然人们在高边坡研究方面已取得了很大的进展,但仍存在大量的未解决的问题,高边坡工程仍作为一种特殊设计而无章可循,所以需要对其不断地进行研究。本文以朱昌河4号主墩所在的岩质边坡为研究对象,对4号桥墩所在岩质边坡的稳定性进行综合分析,并根据分析结果采用预应力锚索及锚杆对其进行加固处理。

1 工程概况

朱昌河特大桥位于沪瑞国道主干线(贵州境)镇胜高速公路K 132+546.443处。桥址区地形为深切“V”型河谷,东西两侧为陡坡地形,东坡坡度35°,西坡坡度40°,相对高差约241 m。桥梁结构形式为(106+200+106 m)预应力混凝土连续刚构桥,4号主墩高达137 m(桥址区位见图1,桥址地形地貌见图2)。

大桥桥址位于旧普安向斜东部,单斜向南缓倾斜,岩层产状165°～200°∠60°～75°,地面裂隙纵横交错,呈网状发育,岩溶发育强烈,突出表现在溶隙、小溶孔及溶洞或落水洞等岩溶状态。地下水的赋存形式以孔隙水、裂隙水为主,水的补给源为大气降水,出露形式以泉点及分散型排泄于朱昌河。岩层岩性主要为三叠系下统永宁针组薄—中厚层状灰岩夹泥质灰岩和钙质泥岩(Tlyn)。

图1 朱昌河特大桥区位图Fig.1 Location of Zhuchanghe grand bridge

图2 桥址区地形地貌图Fig.2 Topography of the bridge site

2 稳定性极限平衡分析

2.1 地质模型概化

朱昌河特大桥4号墩基础地层岩性主要为薄—中厚层状灰岩夹泥质灰岩和钙质泥岩,岩层倾向为165°～200°,倾角60°～75°,岩层走向与坡面走向大角度相交,有利于斜坡的稳定。墩址区主要发育有三组节理裂隙,产状分别为63°～90°∠45°～65°、303°～310°∠12°～45°和265°～285°∠55°～80°[3]。边坡结构面特征及其对稳定性影响情况见表1。

表1 结构面性质及其对边坡稳定性影响Table 1 Structural plane properties and impact on slope stability

根据结构面对边坡的稳定性影响分析,由于层面CM为陡倾角,概化时作为两侧切割面,概化模型简化为沿倾向坡面的缓倾角结构面滑动,倾向坡面的高倾角结构面P2倾角大于坡角,构成后缘拉裂面,倾角取平均值68°;倾向坡面的缓倾角结构面(6°～25°)平均倾角为16°,考虑桥墩桩底高程与坡底位置(两者连线与水平面夹角18°);而倾角越陡,边坡局部岩体稳定性越低,综合考虑倾角取18°(底滑面通过桩底时最大倾角)和25°(底滑面切桩时最大倾角)进行分析。

2.2 岩体力学参数

根据有关岩石力学试验资料以及《工程岩体分级标准》(G B 50218—94),选取岩体力学参数以及对桥基工程岩体进行分级;按照《公路路基设计规范》JTG D 30—2004表4.5.1进行底滑面参数取值;其他参数类比确定。

2.3 边坡稳定性计算

根据大桥结构计算,桥墩承台底处的最不利荷载组合见表2,计算时采取最大弯矩组合:水平力3 561.2 kN,竖向力542 379.1 kN。

表2 承台底处最不利荷载组合Table 2 The worst load combination of the bottom cap

朱昌河特大桥桥基础为一级边坡,按《公路路基设计规范》(JTGD 30—2004),边坡稳定性安全系数正常工况下取Kc=1.20～1.30,暴雨工况下取Kc=1.10～1.20[4]。综合考虑大桥基础的有关地质条件及《公路路基设计规范》(JTGD 30—2004)技术要求,考虑两种可能的滑面(底滑面倾角18°和25°),分别采用极限平衡分析法中的三维极限平衡分析法和不平衡推力法,计算4号桥墩所在边坡在自然状况、加桥荷载、暴雨条件自然边坡、暴雨条件加桥荷载等工况条件下的边坡稳定性系数。桥址区平面图及桩基布置状况见图3。

图3 桥址区平面图Fig.3 Locations of the bridge sites

2.3.1 三维极限平衡方法

运用三维极限平衡方法,模型概化为后缘裂隙贯通,竖向载荷全部作用在底滑面上。在非正常工况(边坡处于暴雨或连续降雨状态下的工况)下,滑面出露处水压力为零,两滑面交点处水压力最大,滑面上水压呈线性分布。由于坡体在自然暴雨状况时是稳定的,故该条件下边坡安全系数取为1.05,进行等效地下水位反算。其中最大水压力P=α γH(α为折减系数)。边坡Ⅱ-Ⅱ′剖面模型及受力示意图见图4。

计算过程中综合参数c、φ值采用加权平均方法确定。

从受力分析可知:

图4 边坡受力示意图Fig.4 Force diagram of the slope

式中:W——边坡岩体重力;Q——竖向桥荷载;T——水平向桥荷载;θ——底滑面倾角;α——侧面水推力与底滑面夹角;P水1——侧滑面水推力,P水1=1/2·P·l1·42;P水2——侧滑面水推力,P水底=1/2·P·l2·42。

根据上述计算公式,可算得桥墩所在边坡在各种荷载组合作用下的稳定性系数及稳定性治理所需的设计加固力。

2.3.2 不平衡推力法

采用《公路路基设计规范》(JTGD 30—2004)提供的不平衡推力法进行计算稳定安全系数和加固力。结合本工程的实际情况,可将桥墩基础划分为2个条块进行计算(如图5所示)。

图5 桥址区Ⅱ-Ⅱ′剖面推力传递法计算图Fig.5 Thrust transfermethod ofⅡ-Ⅱ′profile

稳定安全系数由下式计算所得:

式中:WQi——第I土条的重力与外加竖向荷载之和;α1,αi-1——第I土条底滑面的倾角;ci,φi——第I土条底滑面的粘结力和内摩擦角;li——第I土条底滑面的长度;Ei-1——第I-1土条传递给第I土条的下滑力。

根据上式逐条计算,直到最后一条的剩余推力为零,由此确定稳定安全系数。其中E0=0,迭代算出E2=0,即可求得桥墩基础的稳定安全系数以及满足规范安全要求稳定性系数所需要的加固力。

在推力传递法计算中,滑面综合参数c、φ取值采用加权平均确定。

由上述分析可知,计算公式如下:

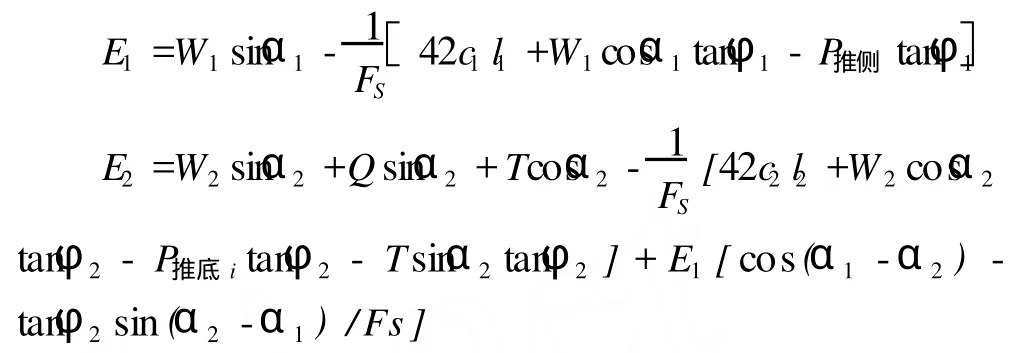
式中:Q——桥竖向荷载;T——桥水平向荷载;α1,α2——滑面倾角。

由给定的参数和计算模型,采用剩余推力法计算滑坡的稳定系数。在计算过程中,首先在剖面条分图上计算出各滑块的面积,滑块滑面长度及各滑块滑面与水平面的夹角;再由各滑块的面积及滑体土的重度求算出各滑块的重量,然后把各已知数据代入相应的计算公式,即可求算出滑坡的稳定性系数。根据上述方法,求得朱昌河特大桥4号桥墩所在岩质边坡在不同工况条件下的稳定性系数。

2.4 稳定性计算结果分析

将三维极限平衡法和不平衡推力法的稳定性计算结果综合分析,分析结果见表3～4。

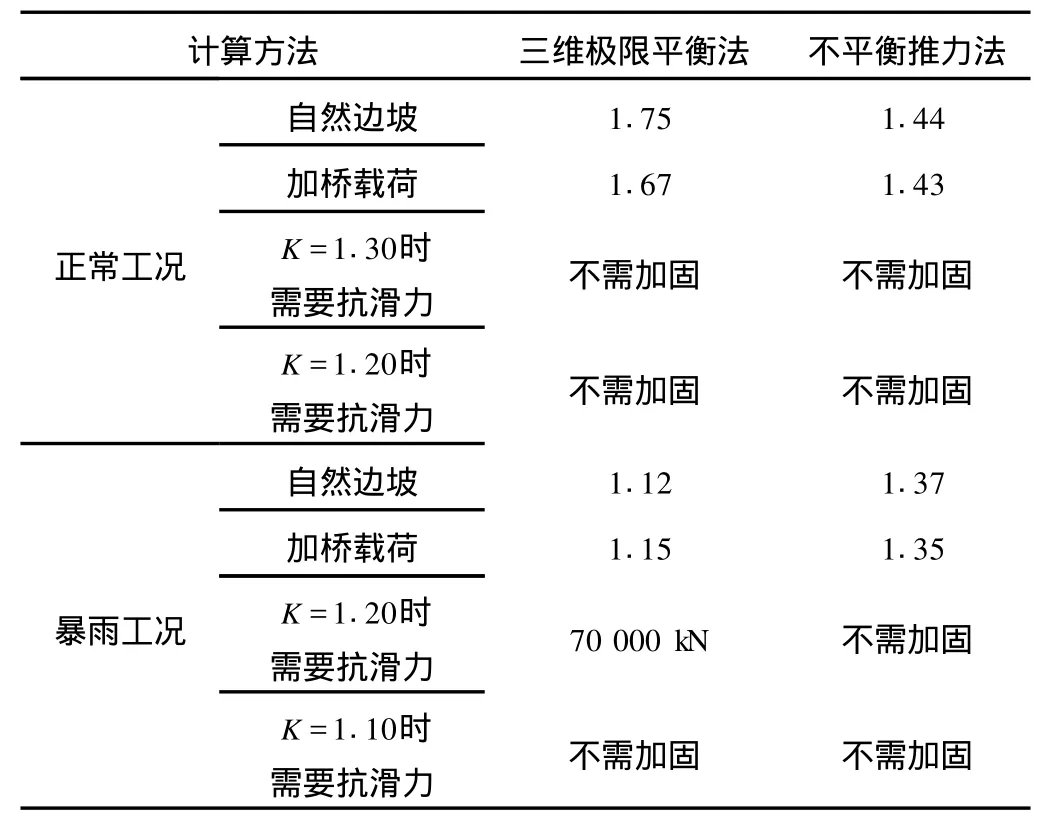
表3 底滑面倾角18°时安全系数和加固力计算成果Table 3 Calculation of the safety factor and the outcome of reinforcement force when the dip angle slipping surface was 18°

表4 底滑面倾角25°时安全系数和加固力计算成果Table 4 Calculation of the safety factor and the outcome of reinforcement force when the dip angle slipping surface was 25°

3 边坡加固设计

通过稳定性计算成果比较分析,朱昌河特大桥4号桥墩所在边坡底滑面倾角为25°时,安全系数取边坡稳定设计标准高值(正常工况取Kc=1.30,暴雨工况取Kc=1.20),需提供220 000 kN的抗滑力,才能保证边坡稳定性达到安全要求;安全系数取边坡稳定设计标准低值(正常工况取Kc=1.20,暴雨工况取Kc=1.10),需提供125 000 kN的抗滑力,才能保证边坡稳定性达到安全要求。

根据稳定性计算结果及桥址区地质条件,安全系数取边坡稳定设计标准低值作为加固设计依据。

底滑面倾角为25°时,设计桥墩桩基穿过滑动面约12 m,因此桩基可以提供部分抗滑力。

根据计算结果,初步拟定承台下部采用压力分散型预应力锚索、坡脚采用锚杆的联合加固方案。

通过计算,结合施工要求,得出预应力锚索的最优安设角为31.5°,设计取30°作为预应力锚索施工安设角。

经计算,在桥墩承台下部边坡设置3排预应力锚索,每根锚索施加预应力1 000 kN,并在坡脚适当设置32锚杆,所提供的加固力能满足边坡加固的需要。由于安全系数取边坡稳定设计标准低值,在施工过程中和大桥运行期间应加强监测工作。

4 边坡稳定性有限元分析

在稳定性计算及加固设计完成后,采用ANSYS软件对本边坡稳定性进行有限元数值模拟分析,对稳定性计算及加固设计的合理性进行验证。

4.1 模拟工况

依据计算模型、计算参数和边界条件等,综合实际工程开挖、加载情况,对边坡在三种工况下的稳定性进行计算模拟:

(1)天然状态 此时边坡处于自然稳定状态,此时只受自重应力作用;

(2)荷载工况 在此工况下,对自然边坡进行了开挖,并施加了桥墩荷载,模拟时采取最大弯矩组合,即水平力取3 561.2 kN,竖向力542 379.1 kN;

(3)支护工况 经极限平衡分析法计算可知,在桥墩荷载下,边坡稳定性达不到安全要求,因此要对边坡进行加固处理。加固方案采取上部锚索、下部锚杆的联合方案进行加固。

图6 天然状态下边坡竖直应力图Fig.6 Vertical stress of the slope in the natural state

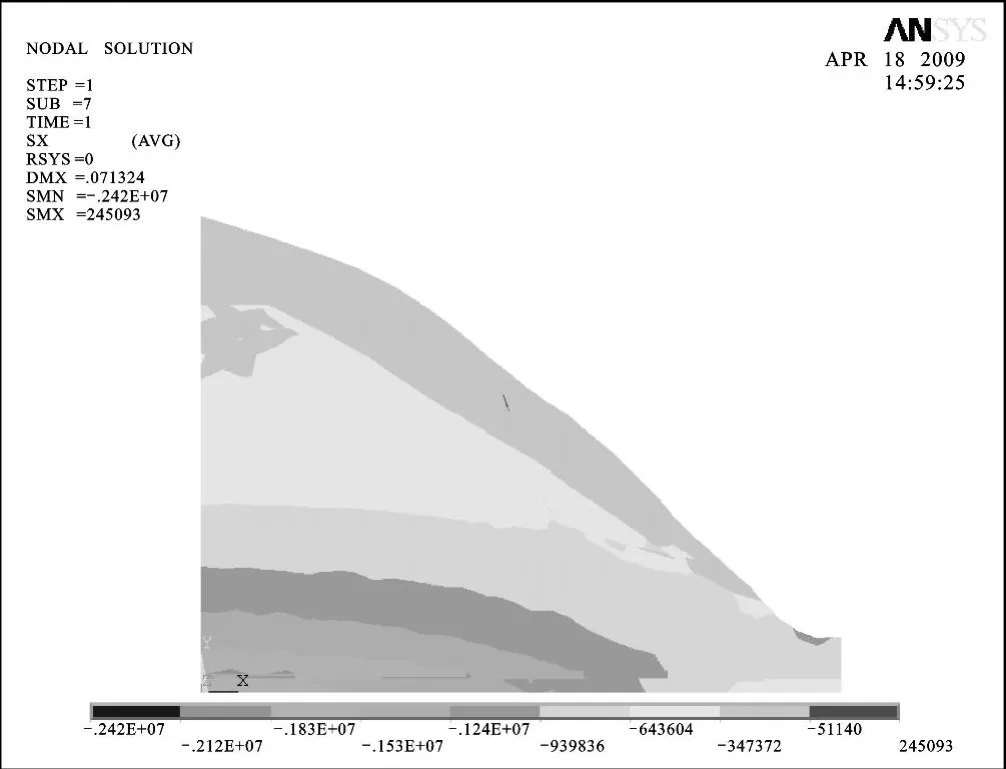
图7 天然状态下边坡水平应力图Fig.7 Horizontal stress of the slope in the natural state

4.2 边坡稳定性模拟

(1)天然状态下边坡稳定性模拟 天然状态下,地应力自地表往深部递增,以压应力为主,坡面卸荷带有一定的拉应力。最大竖直应力和最大主应力水平相当,达5 MPa左右;最大水平应力和最小主应力水平相当,达2 MPa左右。此外,受自重应力作用,后缘拉裂面存在轻微的应力松弛,局部处于受拉状态。天然状态下边坡应力场见图6～7。

按照弹塑性模型计算,天然状态下围岩塑性区主要分布在后缘拉裂面上部和底滑面中下部,其中底滑面塑性程度较深,为潜在主滑面。由于塑性区范围不大,尚未贯通,因此边坡基本处于稳定状态。天然状态下边坡岩体塑性区分布见图8。

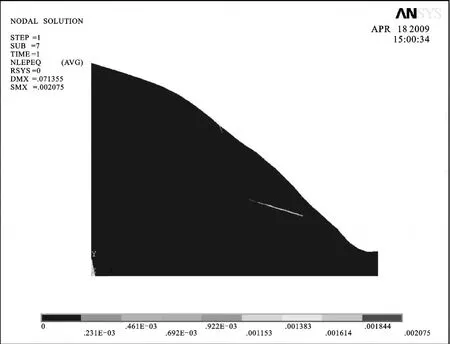
图8 天然状态下边坡等效塑性应变图Fig.8 Equivalent plastic strain of the slope in the natural state

图9 荷载工况下边坡竖直应力图Fig.9 Vertical stress of the slope under load case

(2)荷载工况下边坡稳定性模拟 施加桥墩荷载后,岩体整体应力场变化不大,只在桥墩和桩作用范围附近有局部调整。桩周岩体应力集中明显,而桩下部靠近底滑面范围出现局部应力松弛现象。对比天然状态下的应力分布图可知,由于桥荷载的作用,坡面一定范围内的岩体应力松弛状况有所改善,对坡面岩体稳定有利,但却使后缘拉裂面应力松弛加剧,不利于边坡稳定。荷载工况下边坡应力分布状况见图9～10。

图10 荷载工况下边坡水平应力图Fig.10 Horizontal stress of the slope under load case

根据塑性区计算结果可知,桥荷载施加后,与天然状态相比,后缘拉裂面和底滑面的塑性区范围均有明显扩大,尤以底滑面较突出,几乎沿整个底滑面长度都有塑性区分布,而且越靠近坡脚塑性程度越大,对边坡稳定极为不利。模拟过程中可知,在荷载工况下计算收敛速度很慢,基本处于不收敛边缘,由此可以初步判断,施加桥荷载后,如果没有及时和有效的支护加固手段,边坡极有可能沿底滑面发生滑动,导致边坡失稳。荷载工况下边坡岩体塑性区分布见图11。

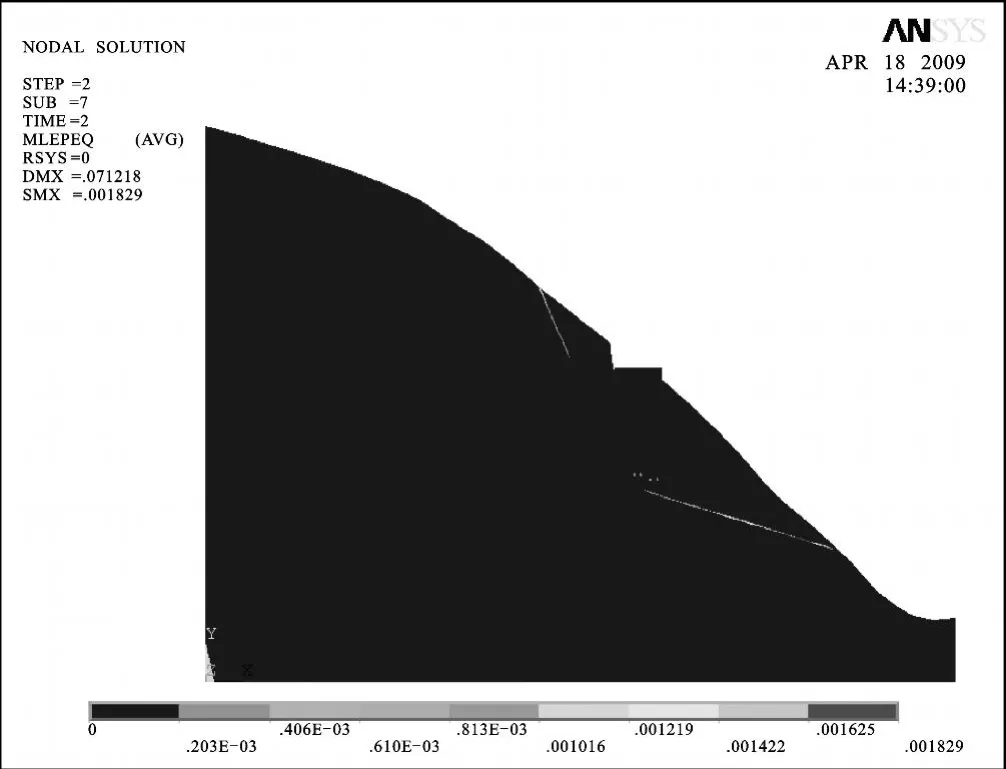
图11 荷载工况下边坡等效塑性应变图Fig.11 Equivalent plastic strain of the slope under load case

(3)支护工况下边坡稳定性模拟 按照上述支护方案对边坡进行加固,所以在模拟过程中可以概化为施加预应力锚索和锚杆后再施加桥荷载。该工况下,与上述荷载工况相比,重分布应力状态相对较为有利,应力分异程度降低,尤其是坡面和后缘拉裂面应力松弛状态显著改善。支护工况下边坡应力场见图12～13。

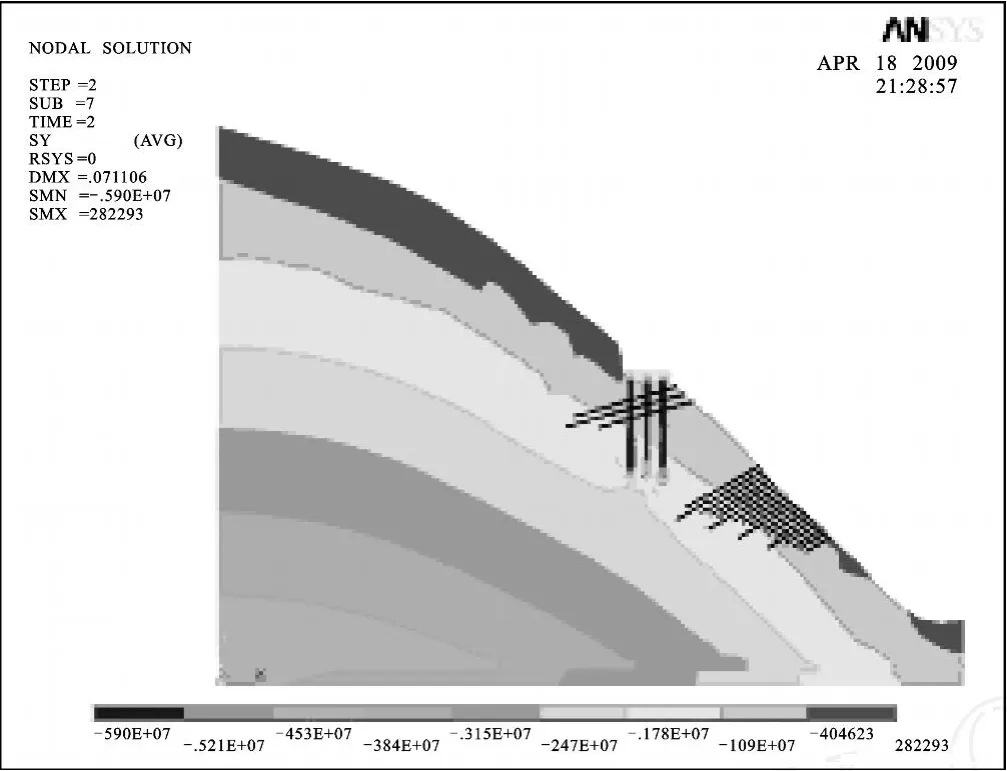
图12 支护工况下边坡竖直应力图Fig.12 Vertical stress of the slope under supporting condition

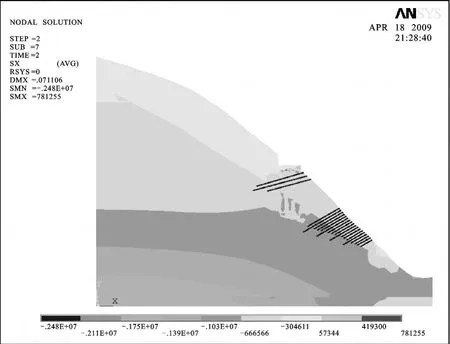
图13 支护工况下边坡水平应力图Fig.13 Horizontal stress of the slope under supporting condition

由边坡等效塑性应变图可以看出,在支护工况下,塑性区比荷载工况下明显减小,且从等效塑性应变图例可知塑性发展程度也明显降低,充分体现了锚索(杆)加固的必要性。综合上述应力、塑性区分布特征,可以判断,采取必要的加固措施后,边坡处于稳定状态。支护工况下的等效塑性应变图见图14。

4.3 数值模拟结果分析

通过对以上三种不同工况下边坡稳定性计算模拟、分析,可以看出:

(1)天然工况下,边坡整体处于稳定状态;

(2)施加设计荷载后,边坡极有可能沿底滑面发生滑动,导致边坡失稳;

(3)施加锚索及锚杆等加固措施后,边坡稳定性得到很大的改善,加固效果明显,边坡处于稳定状态。

计算结果与极限平衡分析法求得的边坡稳定性状态基本一致。

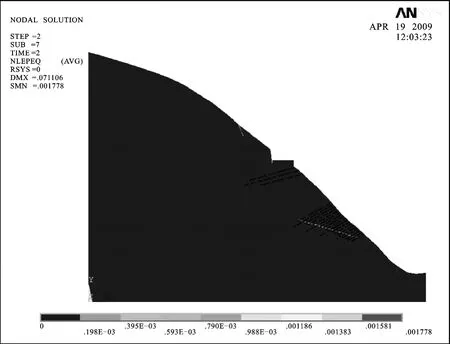
图14 支护工况下边坡等效塑性应变图Fig.14 Equivalent plastic strain of the slope under supporting condition

5 结语

本文以朱昌河特大桥4号桥墩所在边坡为研究对象,通过使用极限平衡方法和有限元分析方法对边坡稳定性进行分析;桥墩所在边坡稳定性主要受地层岩性、地质构造、边坡周边地形地貌等诸多因素的影响;此外大桥施工及运营过程中的附加荷载影响是导致边坡稳定性降低的诱发因素。

通过计算,桥墩所在的边坡在天然工况下整体处于稳定状态,这与现实的情况相符。在边坡开挖及施加桥荷载后,边坡稳定性达不到安全要求;因此,边坡需要进行加固处理。以计算所需的抗滑力作为加固设计的依据,采取上部加锚索、下部加锚杆的联合加固方案进行边坡加固。经验算,加固后的边坡稳定性满足安全要求,边坡由不稳定状态或者极限状态转变为稳定状态,这说明治理方案是有效的。

4号桥墩所在边坡采用上部加锚索、下部加锚杆的联合加固方案进行边坡加固后,自2008年1月通车至今,通过观测,边坡未出现变形、破坏,保证了桥梁运营的安全。

极限平衡分析方法较为成熟,计算结果可信度较高,但运用此法计算边坡稳定性时,边坡的局部位移、塑性区的分布状况不易掌握;而运用有限元数值模拟的方法,边坡位移的大小及应力、塑性区的分布状况非常直观,一目了然。因此,在边坡稳定性计算时,如果将两种方法相结合,不仅能保证计算结果的可靠性,而且能直观地认识到坡体内应力应变的分布状况,在加固设计时可以有的放矢,保证加固方案的合理、经济。

[1] 孙玉科,牟会宠,姚宝魁.边坡岩体稳定性分析[M].北京:科学出版社,1988.

[2] 崔政权.系统工程地质导论[M].北京:水利电力出版社,1992.

[3] 吕江松.朱昌河特大桥4号桥墩补充勘察报告[R].武汉:中交第二公路勘察设计研究院有限公司,2005.

[4] JTGD 30—2004,公路路基设计规范[S].

(责任编辑:胡立智)

Analysis of Slope Stability and Treatment of Zhuchanghe Grand Bridge

XU Zongsu,WU Kaifeng,LONG Ran
(Second Highway Consultants Co.L td.,Wuhan,Hubei430056)

Rock slope is one of the most characteristic engineering geological problems since the 1980s.It’s a non-linear and incertitude dynamic system,so the slope stability analysis and evaluation are complex,further study is needed.Based on the example of the slope near Pier 4 of Zhu Changhe grand bridge,the paper simulates the slope stability using the limit equilibrium method and the finite element method,and adopts prestressed cable anchors and anchors in slope reinforcement.It can also provide a reference for stability analysis of the similar slopes.

slope stability;limit equilibrium method;finite elementmethod

U416.1+4

A

1671-1211(2010)04-0383-07

2010-07-06;改回日期:2010-07-16

徐宗苏(1950-),男,工程师,路桥专业,从事工程地质方面的工作。E-mail:zongsu_xu@163.com