动量及能量转换和守恒的互动式教学＊

朱长军 翟学军 薛 兵

(西安工程大学理学院物理系,陕西西安 710048)

动量及能量转换和守恒的互动式教学＊

朱长军 翟学军 薛 兵

(西安工程大学理学院物理系,陕西西安 710048)

本文通过子弹与木块的碰撞过程中作用力和反作用力做功不相等的例子,详细分析了该力学系统在整个过程中动量及能量的转换和守恒.同时,针对这个问题课堂上采用互动式的讨论,使学生更加深入理解动量及能量转换和守恒的本质,收到了良好的教学效果.

做功;动量;能量;转换和守恒

1 引言

动量和能量守恒是自然界最普遍、最基本的重要规律,无论宇观、宏观、介观和微观系统,动量和能量守恒定律都普遍适用[1].因此,使学生深入理解和掌握动量和能量守恒定律对学生分析和解决与之相关的问题具有极大的促进作用.本文通过一道子弹与木块的碰撞过程中作用力和反作用力做功不相等的例题,详细分析了该力学系统在整个过程中动量及能量的转换和守恒.同时,在课堂上针对这个问题采用互动式的讨论,从而达到使学生更加深入理解动量及能量转换和守恒定律的目的,显著地提高了教学效果.

2 例题及详解

例题 设质量为 m=5.6g的子弹A以 v0=501m/s的速度水平射入一静止在水平面上的质量为M=2kg的木块B内,A射入B后,B向前移动了S=50cm后而停止,求:(1)B与水平面间的摩擦系数;(2)木块对子弹所做的功W1;(3)子弹对木块所做的功W2.

首先,让我们分析整个过程.以子弹和木块组成的系统作为研究对象,整个过程可以分为两个过程,第一个过程是完全非弹性碰撞过程,从碰撞开始直至子弹和木块达到相同速度为止;第二个过程是子弹和木块以相同的速度运动直至停止.图1给出了三个特定的运动状态.状态1到状态2为第一个过程,状态2到状态3为第二个过程.

图1 三个特定的运动状态

第一个过程中,子弹和木块发生完全非弹性碰撞,子弹和木块组成的系统受到的外力是:重力、水平面的支持力以及水平面的摩擦力.系统受到沿竖直方向的合外力为零.水平面的摩擦力在此成为净合外力.但是,此摩擦力远远小于子弹和木块之间的作用力,同时,碰撞过程的作用时间非常短,所以,我们能够近似地认为在这一过程中以子弹和木块组成的系统在水平方向动量守恒[2].第二个过程中,以子弹和木块组成的系统受到的净合外力是水平面的摩擦力.摩擦力是恒力,因此,这一过程是匀减速直线运动过程.

解题的第一步,求B与水平面间的摩擦系数.

设状态2中子弹和木块的共同速度为V2,对第一个过程,根据动量守恒定律,有

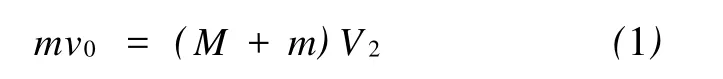
解得V2=1.4(m/s).在这一过程中,子弹的速度急剧减小,木块的速度增大,二者的加速度都不是恒量.

设 f为木块与水平面间的摩擦力;μ为水平面和木块之间的摩擦系数,对第二个过程运用动能定理,有

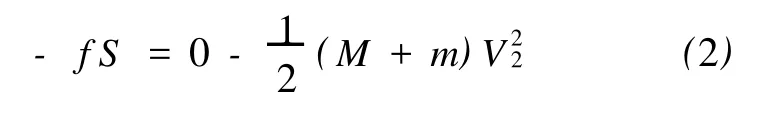
根据摩擦系数的定义

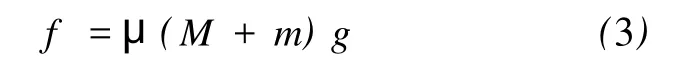
联立式(1)、(2)、(3)解得

解题的第二步,求木块对子弹所做的功W1,有两种方法可以求解.

第一种方法,将子弹作为研究对象,在整个过程中只有木块对子弹做功,根据动能定理,有

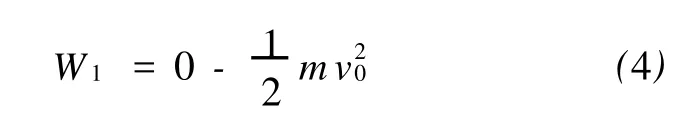
代入数据计算得到W1=-703(J).

第二种方法,仍将子弹作为研究对象,利用动能定理,在两个过程中分别计算木块对子弹做功代入数据计算得到W1=-703(J).

解题的第三步,求子弹对木块所做的功W2.

第一种方法,子弹和木块之间的相互作用力是一对作用力和反作用力.如果子弹和木块发生的位移相同,那么子弹对木块所做的功和木块对子弹所做的功大小相等、符号相反.在本例的第一个过程中,子弹和木块发生的位移不相同,所以必须在两个过程中分别计算子弹对木块做的功.将木块作为研究对象,其在水平方向受到子弹的推力和水平面的摩擦力.第一个过程中,由于子弹的推力远远大于水平面的摩擦力,水平面的摩擦力忽略不计.因此,木块在水平方向受到的合外力可以近似地认为是子弹的推力.根据动能定理,有

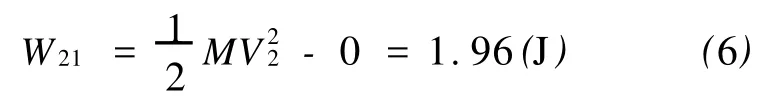
在第二个过程中,子弹和木块发生的位移相同,子弹对木块所做的功和木块对子弹所做的功大小相等、符号相反.所以

整个过程中子弹对木块所做的功为

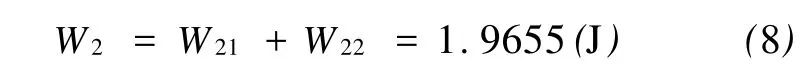
第二种方法,仍将木块作为研究对象,在整个过程中,其初动能和末动能都为零,动能的增量为零.其受到的合外力为子弹的推力和水平面的摩擦力,二者方向相反,二者对木块做的功大小相等、符号相反.第一个过程中,水平面摩擦力的功忽略不计,第二个过程中,根据式(2),摩擦力的功为

此即整个过程中摩擦力对木块做的功,所以子弹对木块做的功为

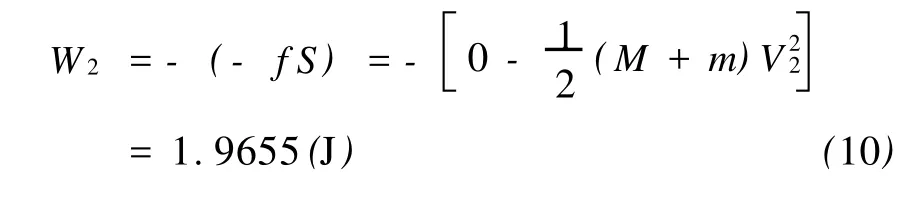
3 课堂上互动式教学

1)学生之间师生之间互动过程.在课堂上,首先复习功的概念及计算方法,接下来复习动能定理,然后给出上述例题.第一步,让三位同学依次分析并求解例题的三个问题,其他同学补充.课堂上发现,同学们对例题的前两问基本能够正确理解和回答,但对第三问,相当多的同学忽略了第一个过程中子弹和木块发生的位移不相同.因此,认为在整个过程中子弹对木块所做的功和木块对子弹所做的功大小相等、符号相反.针对这一现象,给学生举出了一些作用力和反作用力做功大小不等的例子.如,水平面上叠放的两个木块,下面的木块受外力作用,它们在水平面运动,如果两木块之间相对静止,那么它们之间的一对摩擦力(作用力和反作用力)做功相等;如果两木块之间相对运动,那么它们之间的一对摩擦力做功不相等.具体到这一道例题,第一个过程中子弹和木块发生的位移不相同,所以子弹对木块所做的功和木块对子弹所做的功大小不相等.但在第二个过程中,子弹和木块发生的位移相同,因此,子弹对木块所做的功和木块对子弹所做的功大小相等、符号相反.第二步,请学生提问.学生的问题是:是否能够求出第一个过程中子弹和木块发生的位移.对这一问题,给出如下的解答.一般情况下,碰撞过程是一个非常复杂的过程,碰撞体之间的作用力是变力,而且没有一个统一表达式.针对具体的碰撞体的材料以及碰撞体的初速度,经过研究能够得到作用力随时间(或速度、位移)的变化关系,进一步就能够求解碰撞体在碰撞过程中发生的位移.碰撞体之间的作用力随时间的变化关系通常不能用解析函数表示,实际过程中,常常将这种变化关系拟合为某种解析函数,进而求解.

2)教师在课堂的点评与课后的反思

在详细讲解了上述的解题过程后,在课堂上对该力学系统在整个过程中动量及能量的转换和守恒进行分析和总结.

(1)动量及动量守恒.第一,将子弹作为研究对象.在整个过程中,它只受到木块的冲量,因而子弹动量不守恒.第二,将木块作为研究对象.在整个过程中,其初、末动量都为零,说明在整个过程中木块受到子弹和水平面摩擦力的冲量大小相等,方向相反,合冲量为零.但是整个过程木块动量不是恒量,因而整个过程中木块动量不守恒.第三,将子弹和木块作为一个系统.在第一个过程中,木块和水平面之间的摩擦力远远小于子弹和木块之间的作用力,作用时间又非常短,因此摩擦力的冲量忽略不计.在这种情况下,外力的冲量为零,系统动量守恒.在第二个过程中,子弹和木块成为一体,受到摩擦力的冲量(摩擦力的作用时间较长,其冲量已不能忽略),系统动量不守恒.因此,在整个过程中,子弹和木块构成的系统动量不守恒.

(2)能量及能量守恒.第一,将子弹作为研究对象.在整个过程中,合外力为木块的阻力.木块的阻力对其做负功,因而动能不守恒(减少),子弹势能不变,因而整个过程中子弹机械能不守恒.第二,将木块作为究对象.在第一个过程中,摩擦力远远小于子弹对木块的作用力,位移又非常短,因此摩擦力的功忽略不计,子弹的推力对其做正功,木块动能增加.在第二个过程中,子弹的推力和摩擦力分别对其做正功和负功,但大小不相等.但是,整个过程中,子弹的推力和摩擦力对木块做功大小相等、符号相反,最初态和最末态的动能都为零,但是,整个过程木块势能不变,动能不是恒量,因而整个过程中木块机械能守恒.第三,将子弹和木块作为一个系统.在第一个过程中,摩擦力远远小于子弹对木块的作用力,位移又非常短,因此摩擦力的功忽略不计.在第一个过程中,虽然系统的势能不变,但是,由于非保守力(子弹和木块之间的作用力)做功,系统的机械能不守恒.在第二个过程中,系统的势能不变,摩擦力做负功,动能减小.所以.整个过程中,子弹和木块构成的系统的机械能不守恒.那么,机械能哪里去了呢?系统的机械能(动能)通过以上过程中所有非保守力做功全部转化为热能.

(3)动量守恒及能量守恒定律的适用范围.动量守恒定律是牛顿定律的推论,它只在惯性参照系中成立.应用动量守恒定律解决问题时,所有的动量必须都对应于同一个惯性参照系.虽然动量守恒定律是由牛顿定律导出的,但动量守恒定律是比牛顿运动定律更普遍、更基本的定律,它在宏观或微观领域范围内、低速或高速情况下均适用[3].机械能守恒的条件是力学系统外力的功与系统内非保守力的功的代数和为零.但是,能量守恒定律则指明了孤立系统能量的转移和转化,而系统总的各种形式的能量的总和守恒.因而,它比机械能守恒的应用范围更加广泛.

课后的反思.互动式教学应将以下几个方面有机地结合起来:基本理论知识的传授、互动选材的给出、学生之间师生之间互动、教师的点评.在以上几个方面中,至为重要的最能显现课堂教学特征的是学生之间、师生之间的课堂互动行程.在互动式教学过程中,既要考虑学生的理解和接受能力,又要考虑选材的展开深度与广度,同时还要兼顾学生参与课堂互动过程的积极性和主动性.总之,量体裁衣地选用互动模式才能确保教学互动流程的顺畅,才能激发学生积极地思考问题,才能提高学生的学习效果.

4 结论

采用互动式教学讲授碰撞过程中作用力和反作用力做功、动量及能量转换和守恒定律的应用.用一道例题说明在两个物体位移不相等时,它们之间的作用力和反作用力做功不相等.同时,使学生理解动量守恒定律在系统外力的冲量非常小时也能够近似成立.用能量守恒定律分析了系统机械能和热能之间的转换.加深了学生对动量守恒及能量守恒定律的理解,收到了非常好的教学效果.

[1] 马文蔚,解系顺,谈漱梅.物理学[M] 第四版.北京:高等教育出版社,1999.63～64

[2] 吴百诗,焦兆焕,张孝林.大学物理基础[M].北京:科学出版社,2007.110～112

[3] 高景,李铜忠,董占海.大学物理学[M] 第四版.上海:上海交通大学出版社,2009.76～80

2009-06-10)

西安工程大学大学物理精品课程基金项目.