基于模糊滑模的卫星姿态控制系统故障诊断
樊 雯 程月华,2 姜 斌
(1南京航空航天大学自动化学院,南京210016)(2南京航空航天大学高新技术研究院,南京210016)
基于模糊滑模的卫星姿态控制系统故障诊断
樊 雯1程月华1,2姜 斌1
(1南京航空航天大学自动化学院,南京210016)(2南京航空航天大学高新技术研究院,南京210016)
针对卫星姿态控制系统的执行机构故障,提出了一种基于T-S模糊方法和滑模观测器的故障诊断方法.首先,建立了基于T-S模糊模型的卫星姿态控制系统模型,并在此基础上,设计了一种用于状态检测的模糊滑模观测器.该观测器在执行机构发生故障的情况下,仍然保持滑模模态,可以利用等效输出注入实现故障的直接估计.在故障和干扰上界未知的情况下,采用迭代学习算法在线计算并调节滑模项的切换增益大小,避免了不必要的高频抖振现象;同时利用H∞思想,通过求解LMI获得观测器参数,将干扰对故障估计的影响最小化.计算机仿真结果表明,该故障诊断方法能够对执行机构故障进行较为精确的估计,从而验证了方法的有效性.
卫星;姿态控制;故障诊断;T-S模糊模型;滑模观测器
近年来,随着空间技术的发展,对卫星姿态控制系统的可靠性和自主运行能力有了更高的要求.卫星姿态控制系统的故障诊断技术研究,对切实保障其可靠性与安全性具有重要意义.作为故障诊断方法的一种,基于模型的故障诊断方法应用较多,但需要以精确的数学模型为基础,构造观测器产生残差,继而进行故障的评价与决策.大多基于模型的故障诊断方法都是针对线性系统的,对于非线性系统,缺乏统一可行的方法.
由于正交试验结果中的最佳因素水平组合未在试验中出现,我们在上述条件下进行了验证试验,结果见图5。试验组的颜色评分为91.2,优于前期的各组试验,表明正交试验的结果正确。此外,通过对最优方案组的赖氨酸含量和还原糖含量显著高于企业原始配方组,但蛋白质、脂肪和总糖等主要营养物质的含量无显著差异。
Takagi等[1]提出的T-S模糊建模方法,利用多个局部线性模型模糊逼近非线性系统模型,既考虑了系统本身的非线性特征,又降低了观测器设计问题的困难性与复杂性.该方法已被用于解决许多非线性系统故障观测器的设计问题[2].
滑模观测器因其对系统中的干扰、未建模动态等不确定因素具有鲁棒性而被越来越多地应用于故障诊断中[3~6].Edwards等[3]提出了一种基于滑模观测器的故障诊断策略:在故障发生时,观测器仍然保持滑动模态,故障信号可通过构造等效输出注入项得到重构.这一方法避免了产生评价残差的复杂性.使用这种策略时,需要已知故障与外部干扰的上界.在实际应用中,过大的切换增益会引起不必要的高频抖振.减小抖振的方法有2种:①采用饱和函数代替滑模项中的符号函数[7];②自适应地估计系统干扰和故障的上界[8]或者构造一个自适应的切换增益[9],这样就不必已知干扰和故障的上界.
本文基于T-S模糊模型,设计了一种滑模观测器,用于研究卫星姿态控制系统反作用飞轮的故障诊断问题.利用等效输出注入直接对故障进行估计,并通过LMI求解合适的设计参数来最小化干扰对故障估计的影响.在系统干扰和故障上界未知的情况下,采用迭代学习算法,对滑模项切换增益进行在线计算与调节,同时可避免不必要的高频抖振.
各种影像中有关大运河的记录,也不过百年,但这些记录,却写满了沿岸人民的回忆……今天,我们就走进运河岸边的江北水城——聊城,听一听她的运河故事。
1 系统描述
1.1 卫星姿态的动力学和运动学方程
三轴配置反作用飞轮的刚体卫星姿态动力学方程可表示为
学校、企业各方要有主人翁的姿态,要充分认识到自身在产教融合中的重要作用,应整合自身的优势资源,明确各自的身份、任务和使命,共同培养学生的职业核心能力,使学生能更快、更好地掌握烹饪技能,为将来快速适应工作环境打下坚实基础。
爱茉莉太平洋财报显示,2018年第二季度化妆品营业利润为8.9亿元,同比增长43.5%,以雪花秀、赫妍为代表的高端品牌及海外市场的增长被认为是拉动业绩的重要引擎。另据欧睿调查显示,爱茉莉太平洋旗下的洗发品牌“吕”2018年1-4月在中国市场销售额同比增长了约45%,2014—2017年其在中国的销售额增幅达到了9 521%,年均激增358%。

式中,J为卫星的惯量矩阵;ω={ωx,ωy,ωz}T为星体相对与惯性空间的角速度在本体坐标系中的投影矢量;hω为飞轮角动量;Lc为飞轮控制力矩;Ld为各种干扰力矩总和.
式中,k表示t时刻的迭代次数;Φ表示决定了迭代收敛速率的正定增益矩阵表示对向量的每一个元素取绝对值,2个向量之间的点乘仍为一个向量,其元素为2个向量对应元素的乘积.

令ωr={ω1,ω2,ω3}T为卫星姿态相对轨道坐标系的转动角速度在星体坐标系下的投影.ω与ωr的关系为为轨道坐标系到星体坐标系的转换矩阵,ωo为轨道角速度.
定义状态变量 x={φ,ωx,θ,ωy,ψ,ωz}T,输出 y={ωx,θ,ωy,ωz}T.根据式(1)和(2),可定义如下的系统方程:
如图1所示,目标区域是一个L×W的矩形区域,网格法将目标区域用平行于x轴和平行于y轴的一系列等间距直线划分成一个个的网格,网格间的距离称为粒度d,由期望的覆盖判断精度所决定。

式中,u为控制力矩.
1.2 T-S 模糊模型
T-S模糊模型通过一系列IF-THEN规则下的多个局部线性模型模糊逼近非线性系统,本文给出的T-S模糊模型描述如下:
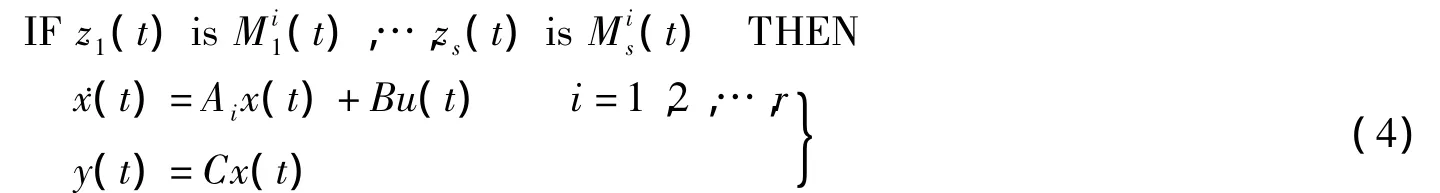
式中,Gli和Gni为适维增益矩阵;vi为引起滑模运动的滑模切换项.
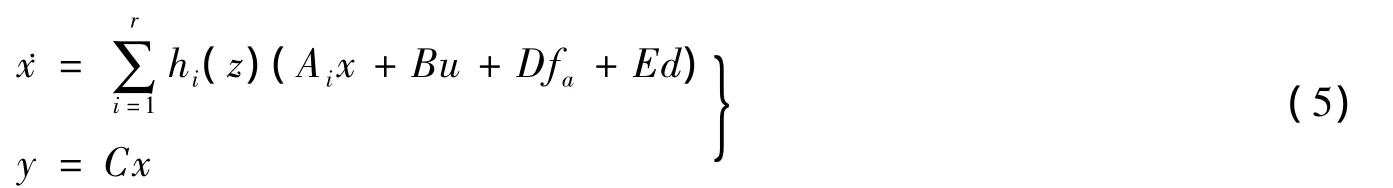
式中,fa为执行机构故障;d为外部干扰其中
2 模糊滑模观测器设计
2.1 观测器设计
考虑式(5)所示的不确定动态系统,其中,B∈Rn×q;C∈Rp×n;E∈Rn×k;n >p > q.
对于此系统,假设满足:① (Ai,C)可观测,且i=1,2,…,r;② 存在已知函数α(t,u)和已知常数β,使得‖fa(x,t)‖≤α(t,u),‖d‖≤β;③ rank(CD)=rank(D),且(Ai,D,C)的任意不变零点都位于左半平面.
根据PDC原则,提出如下形式的滑模观测器:
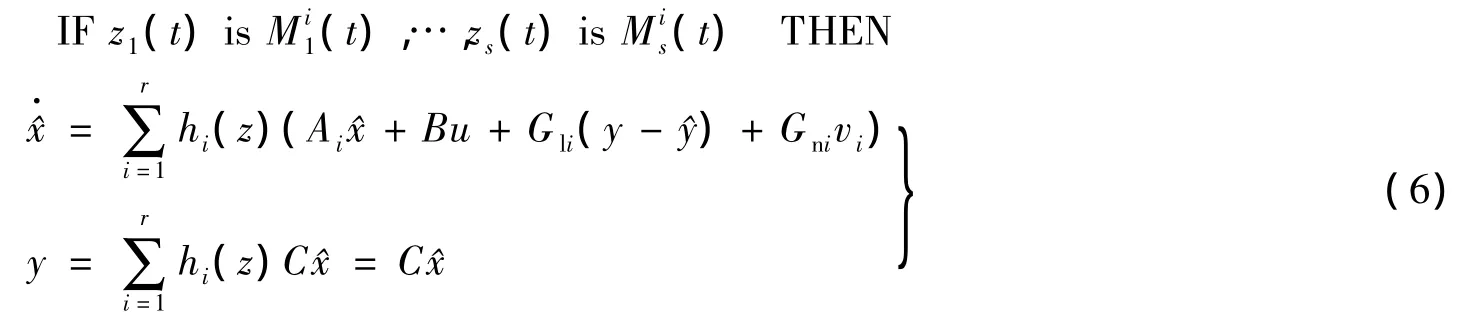
式中,z1,z2,…,zs为先验变量为隶属度函数;r为模糊规则数;s为先验变量数;Ai通过对式(3)在工作点线性化得到.考虑执行机构故障,整个系统的状态方程可表示为
根据文献[10]的描述,存在一个线性非奇异坐标变换T0,使得系统具有如下的结构:
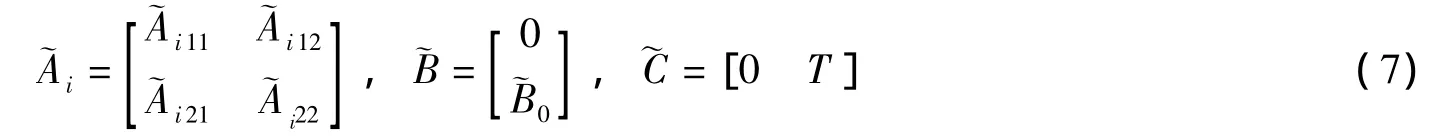
由定理2可知,系统产生滑模运动,则ey=˙ey=0.在式(7)所示的坐标系下将式(11)改写为
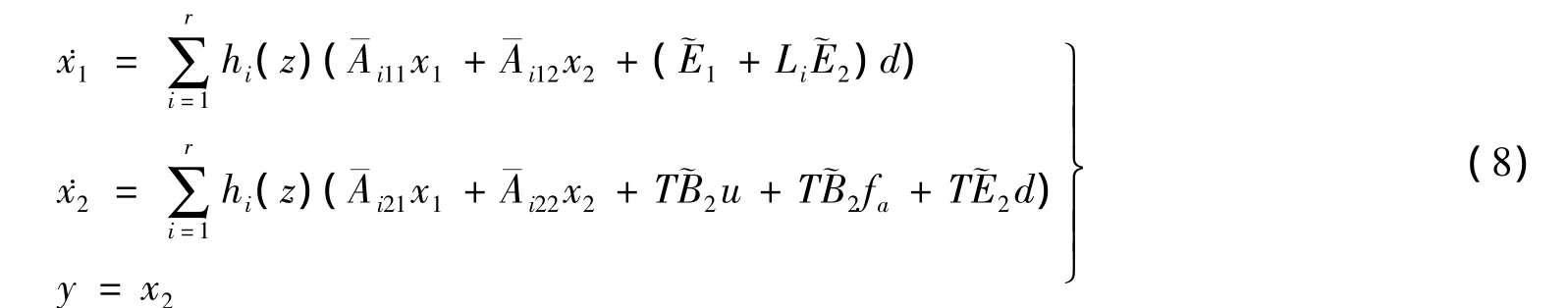
定义ey=-y,则矩阵为稳定的设计矩阵,P2i为其Lyapunov矩阵.切换函数vi定义为
在此坐标系下,设如下的计滑模观测器:
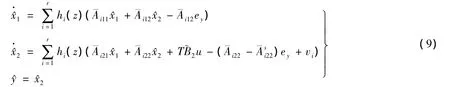

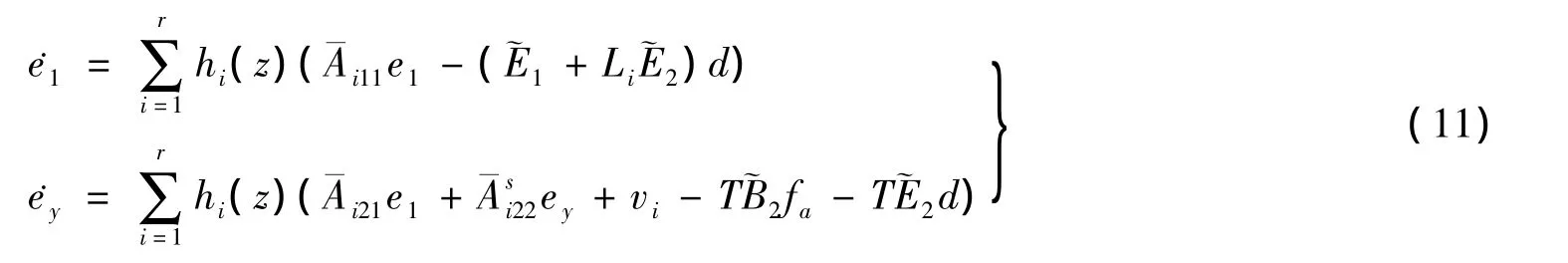
定理1 设P1i为满足的正定Lyapunov矩阵,定义正数,则状态误差e1最终被限制在集合中,其中 ε >0 为任意小的正数.
证明 参见文献[10].
由定理1知,‖e1‖<2μ1β/μ0+ε.根据ρ的定义,有.这就证明了输出估计误差将在有限时间内达到0,产生滑模运动.于是有增益矩阵
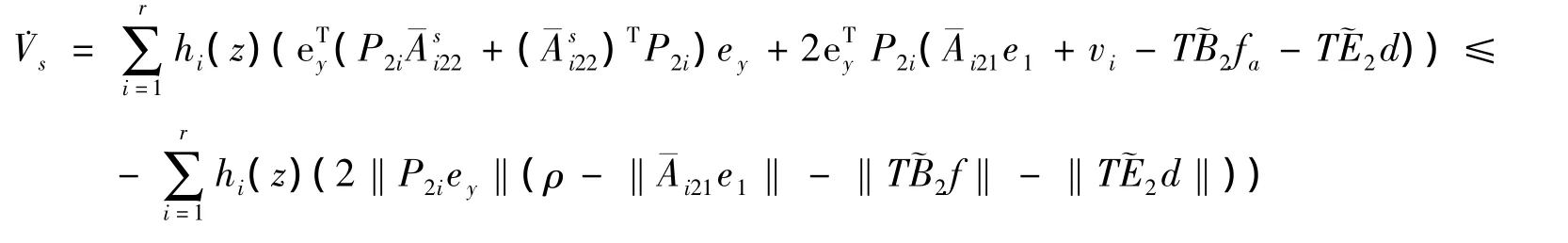
2.2 滑模项切换增益的优化
上述滑模观测器是在已知系统干扰与故障上界(在实际应用中往往并不已知)时进行设计的,其切换增益ρ对应了最坏的情况,从而保证观测器在故障发生时仍然保持滑动模态.但这样可能会导致切换增益过大而引起不必要的高频抖振.故考虑寻找一个时变的滑模项切换增益,既不是太大也不至于过小(切换增益太小可能会导致无法到达滑模面),且无需提前已知干扰与故障的上界值.下面给出一个切换增益的迭代学习算法,即
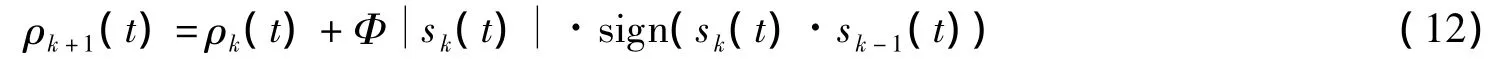
北运河流域全境共划分为346条小流域,其中山区37条,平原286条,山区—平原21条。按照北京市水土保持类型区划分,北运河流域地跨北京市全部4个类型区,其中城市径流控制区 2 434km2,含224个小流域;地下水源涵养区757km2,含72个小流域;地表水源涵养区735km2,含34个小流域;土壤侵蚀控制区320km2,含 16 个小流域(见图1)。
1.1.2 科室管理 开展经尿道前列腺等离子电切术应由具备外科手术资质的临床科室承担。多数医院由独立建制的泌尿外科开展。没有按照系统分科的医院,需要外科中从事泌尿外科方向的医师团队承担。掌握该项技术需要一定的学习曲线,因此,科室应该选派专人前往已经熟练掌握该技术并具备培训或质量控制资质的区域医疗中心进修学习。
根据算法(12)可以看出,如果系统没有到达滑模面,此时希望增益大一些;当sign(sk(t)·sk-1(t))的元素为+1时,切换增益就会增大.如果系统穿过了滑模面,此时希望增益小一些;当sign(sk(t)·sk-1(t))的元素为-1时,切换增益就会相应地减小.在理想状况下,通过迭代更新切换项增益,获得每个时刻t的最优切换增益,使得sk(t)到达滑模面上.在实际计算中,为了防止计算时间过长,可设定一个k的最大值.可以证明,当Φ选择合适时,该迭代算法的收敛性可以得到保证[11].
教师的教育信念是教师专业发展的重要内容,是教师专业结构的有机组成部分,在教师专业结构中位于较高层次,统领着教师专业结构中的其他方面[1]。
3 故障估计

式中,vieq为等效输出误差注入项,可近似表示为vieq=-ρ(P2iey/‖P2iey‖+δ),其中δ是一个很小的正数.
水煎300 ml,1/日剂,分服2次。10天一个疗程,疗程间隔3天,继续下一疗程。6个疗程后评估疗效。
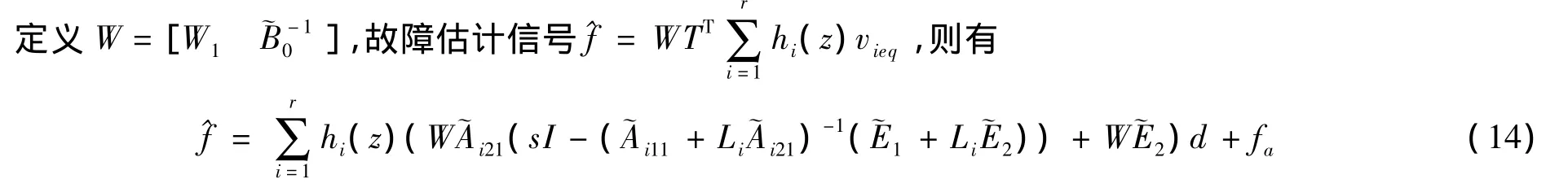
参照文献[10],如果
奴婢不吵你了便是。云梦善解人意地说,我和妈看电视时,尽量不出声,让你早成大师……真是的,在自己家,竟还不允许放开笑了。
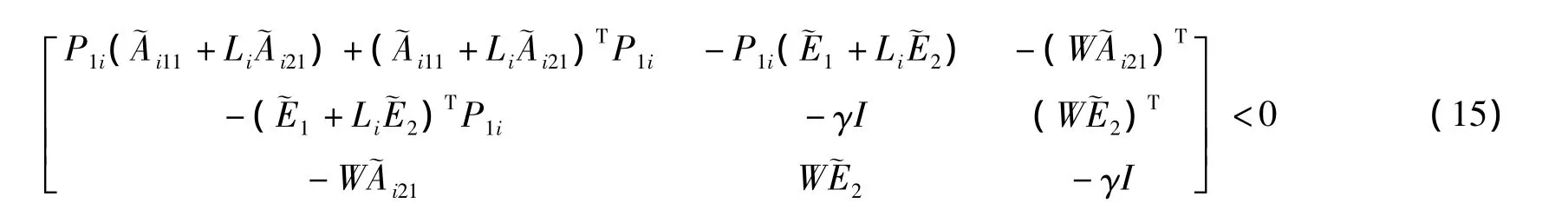
4 仿真结果
对卫星姿控系统的反作用飞轮故障进行仿真研究,验证本文提出的故障诊断方法的有效性.卫星转动惯量J和干扰前的分布阵E可分别表示为
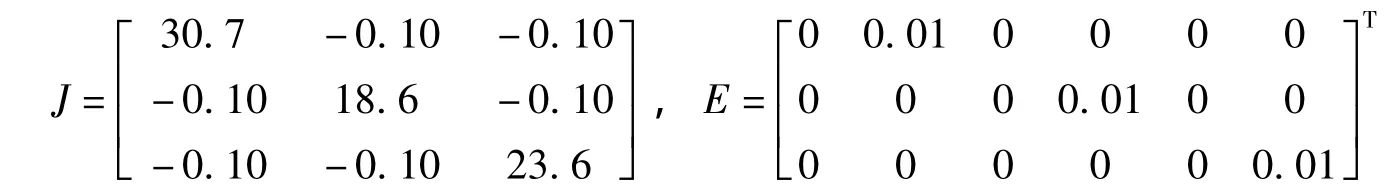
干扰为 d(t)={A0(3cos(ωot)+1),A0(3cos(ωot)+1.5sin(ωot)),A0(3sin(ωot)+1)}T,其中 A0=1.5×10-5,ωo=0.001 1为轨道角速度(rad/s).
令 ωx,ωy,ωz为先验变量,选择如下9 个工作点:xo0={5,0,5,0,5,0}T, xo1={5,0.02,5,0.02,5,0.02}T, xo2={5,0.02,5-0.02,5,0.02}T, xo3={5-0.02,5-0.02,5,0.02}T,xo4={5-0.02,5,0.02,5,0.02}T, xo5={5,0.02,5,0.02,5-0.02}T,xo6={5,0.02,5-0.02,5-0.02}T, xo7={5-0.02,5-0.02,5-0.02}T,xo8={5-0.02,5,0.02,5-0.02}T.
随着资源和环境的约束不断增强,能源和劳动力等要素成本不断上升,高投入、高耗能、低技术含量的传统发展模式逐步退出了工业发展的舞台。科技日新月异的发展,助推智能化工厂发展的步伐,通过信息化,智能化改造现有的工作模式,变粗放生产为集约式精益生产,实现设备之间的互联互通,由传统生产线向数字化、智能化生产线升级是未来工厂发展的必然趋势。
在上述条件下,求得γ最小为0.307,切换增益迭代次数上限为250.图2为飞轮三轴故障的实际值与估计值.三轴故障可分别表示为
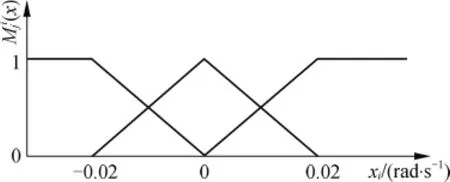
图1 隶属度函数
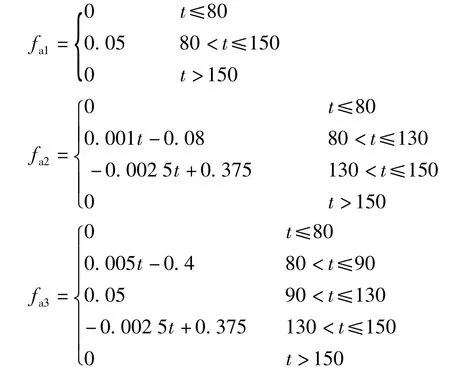

图2 飞轮三轴故障的实际值与估计值
从仿真结果可以看出,对于飞轮的恒偏差故障和恒增益故障,滑模观测器可以做出精确的估计.在初始时刻附近,估计信号与故障信号有较大的初始误差,这是因为在观测器跟踪系统过程中滑模项主要用于抵消状态误差.
5 结语
本文针对卫星姿态控制系统执行器故障,提出了一种基于T-S模型的滑模观测器,通过等效输出注入直接对故障进行估计.通过迭代学习算法在线调节滑模项切换增益大小,避免必须已知故障与干扰上界的要求;利用H∞的思想求解观测器参数,最小化干扰对故障估计的影响.仿真结果表明,该故障诊断方法能够实现故障的检测与估计,将来还可以在此基础上设计容错控制.
References)
[1]Takagi T,Sugeno M.Fuzzy identification of systems and its applications to modeling and control[J].IEEE Trans Syst Man Cybern,1985,15(1):116-132.
[2]Chen W T,Saif M.Design of a TS based fuzzy nonlinear unknown input observer with fault diagnosis applications[C]//Proceedings of the 2007 American Control Conference.Washington,DC,USA,2007:2545-2550.
[3]Edwards C,Spurgeon S K,Patton R J.Sliding mode observers for fault detection and isolation[J].Automatica,2000,36(4):541-553.
[4]Jiang B,Staroswiecki M,Cocquempot V.Fault estimation in nonlinear uncertain systems using robust sliding-mode observers[J].IEE Proc Control Theory Appl,2004,151(1):29-37.
[5]陈茂银,周东华.一类非线性系统的故障诊断[J].自动化学报,2004,30(6):1011-1016.Chen Maoyin,Zhou Donghua.Fault detection and isolation in a class of nonlinear systems[J].Acta Automatica Sinica,2004,30(6):1011-1016.(in Chinese)
[6]刘京津,姜斌.基于滑模观测器的故障诊断技术在飞控系统中的应用[C]//2007年中国控制与决策学术年会论文集.苏州,2007:605-610.Liu Jingjin,Jiang Bin.Sliding mode observers-based fault detection and isolation in flight control systems[C]//Proceedings of 2007 Chinese Control and Decision Conference.Suzhou,2007:605-610.(in Chinese)
[7]张娴,程月华,姜斌.滑模观测器和变结构控制的小卫星姿态控制系统设计[C]//第27届中国控制会议论文集.昆明,2008:141-144.Zhang Xian,Cheng Yuehua,Jiang Bin.Sliding mode observer based variable-structure control in attitude control system of small satellite[C]//Proceedings of the 27th Chinese Control Conference.Kunming,2008:141-144.(in Chinese)
[8]Wheeler G,Su C Y,Stepanenko Y.A sliding mode controller with improved adaptation laws for the upper bounds on the norm of uncertainties[C]//Proceedings of the 1997 American Control Conference.Albuquerque,New Mexico,USA,1997:2133-2137.
[9]Monsees G,Scherpen J M A.Adaptive switching gain for a discrete-time sliding mode controller[C]//Proceedings of the 2000 American Control Conference.Chicago,Illinois,USA,2000:1639-1643.
[10]Tan C P,Edwards C.Sliding mode observers for robust detection and reconstruction of actuator and sensor faults[J].Int J Robust Nonlinear Control,2003,13(5):443-463.
[11]Wu Q,Saif M.Robust fault diagnosis for a satellite system using a neural sliding mode observer[C]//Proceedings of the 44th IEEE Conference on Decision and Control and European Control Conference ECC.Seville,Spain,2005:7668-7673.
Fault diagnosis in attitude control system of satellite based on fuzzy sliding mode
Fan Wen1Cheng Yuehua1,2Jiang Bin1
(1College of Automation Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)(2Academy of Frontier Science,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
A fault diagnosis approach based on the Takagi-Sugeno(T-S)fuzzy and the sliding mode observer is proposed for actuator faults in the attitude control systems of a satellite.First,an attitude control system model of the satellite is constructed based on the T-S fuzzy and a sliding mode observer is proposed for state detection.The observer can maintain a sliding motion even in the presence of actuator faults;thus,the estimation of the faults can be directly achieved by equivalent output injection.When the upper bounds of the faults and disturbances are unknown,an iterative learning algorithm is used to calculate and update the switching gain of the sliding mode term,avoiding unnecessary chattering.And by using the concepts of H∞,a linear matrix inequality(LMI)is calculated to minimize the effects of disturbances on the estimation of the faults.The results of the numerical simulation show that the accurate estimation of the actuator faults can be obtained,which proves the effectiveness of this approach.
satellite;attitude control;fault diagnosis;Takagi-Sugeno(T-S)fuzzy model;sliding mode observer
TB277
A
1001-0505(2010)增刊(I)-0238-06
2010-05-10. 作者简介:樊雯(1989—),女,硕士生;姜斌(联系人),男,博士,教授,博士生导师,binjiang@nuaa.edu.cn.
江苏省自然科学基金重点资助项目(BK2010072)、南京航空航天大学研究生创新实验室基金资助项目、南京航空航天大学大学生创新基金资助项目.

