基于多观测器的无人机切换式故障诊断与调节
陆玲莉 姜 斌 杨 浩
(南京航空航天大学自动化学院,南京210016)
基于多观测器的无人机切换式故障诊断与调节
陆玲莉 姜 斌 杨 浩
(南京航空航天大学自动化学院,南京210016)
基于无人机的非线性模型,提出了一种新颖的切换式故障诊断与调节方案,构造出一组带有不同故障估计初始值的故障诊断机制及其切换律,以提高系统的故障估计和容错控制性能.该方法在单个自适应观测器的思想上,设计出多个自适应观测器以进行故障估计,并根据实际故障范围划分成多个故障区域,针对每个故障区域设置不同的故障估计初始值;同时根据不同的性能要求,设计出相应的控制切换律,使系统在该切换律的作用下,通过输出误差最小原则切换到最优的故障诊断机制.选择该最优故障诊断机制产生的状态观测值和故障估计值,用于设计容错控制器中的反馈控制量.该方法提高了故障诊断的快速性和容错控制过程中的状态性能.最后,对一个无人机系统进行仿真研究,结果验证了该方法的有效性.
无人机;切换式故障诊断与调节;容错控制
无人机成本低,无人员伤亡风险,生存能力强,机动性能好,在现代战争中有极其重要的作用,主要执行战略侦察、监视、空中预警、通信中继和电子干扰等任务;在民用领域更有广阔的应用前景.然而,以往的低可靠性记录以及缺乏明确的规章制度,使得无人机的整体性能下降.近期研究表明,无人机飞行控制系统中易发生故障的部位包括航空电子设备、大气数据系统、伺服作动器、控制舵面、机载软件、导航系统和其他相关子系统[1].因此,如何提高无人机的耐用性、可靠性是该研究领域的热点,在早期阶段引入故障诊断和故障调节策略是保证无人机可靠飞行的关键.然而,由于无人机的重量、大小和成本的限制,多重硬件冗余的方法不能很好地满足该要求,只有结合主动容错控制的思想才能很好地解决上述问题[2-3].
本文考虑无人机执行器故障,采用基于自适应观测器的方法,对无人机非线性模型进行故障估计,并设计了容错控制器.由于传统的故障估计初值一般设置为0,当该值偏离故障真实值不大时,其估计效果是较好的;当该值偏离故障真实值很大时,所需的估计时间也会增大,这与系统对估计快速性的要求是相悖的.因此,本文将传统的故障诊断机制进行扩展,构造出一组带有不同故障估计初始值的故障诊断机制及其切换律,系统在该切换律下,选择当前输出误差最小的诊断机制产生的状态和故障估计值,作为最优反馈量,用于构造容错控制器,从而有效地提高了故障诊断的快速性和容错控制过程中的状态性能.
1 系统描述
无人机非线性动态模型如下[4]:

2 自适应故障估计
故障调节的依据是故障估计值.假设故障发生后在t0时刻被检测出来,具体工作参见文献[5].在故障检测后[5],只有得到快速准确的估计项才能得到有效的附加控制律,因此故障估计是故障调节的一个难点.
假设1 存在一个矩阵K,使得G(s)=C[sI-(A-KC)-1E]满足严格正实条件,即

该假设成立的一个必要条件是(A,C)可观,且rank(CE)=q.
推论1[6]基于假设1,对于任意给定的矩阵Qn×n>0,标量ε >0,存在2 个矩阵Pn×n>0,Rr×q>0,使得
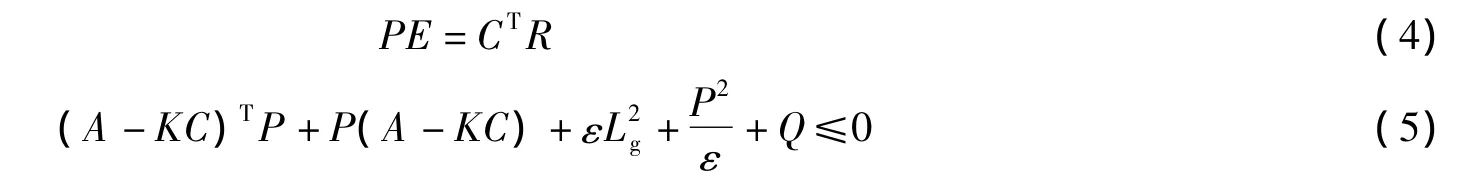
得到上述参数K和R后,对系统(2)设计如下的自适应观测器:
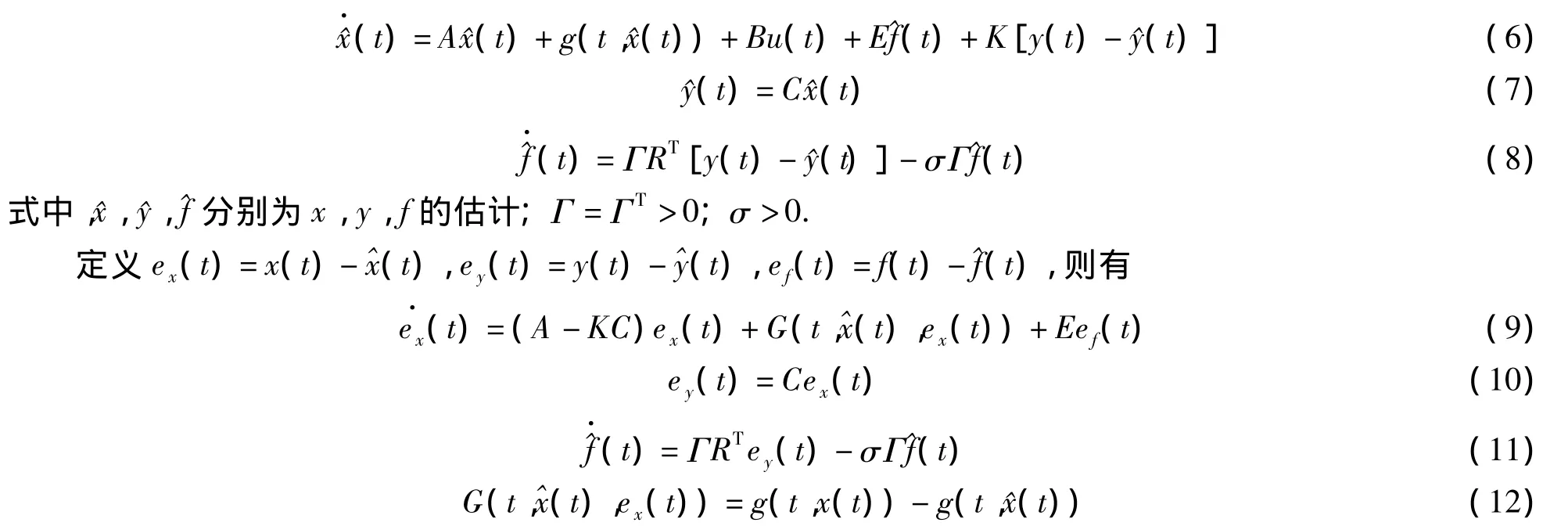
定理1[7]如果系统(2)满足假设1,则自适应观测器(6)~(8)能保证(ey(t),^f)指数收敛到S,且收敛速度大于 e-αt.
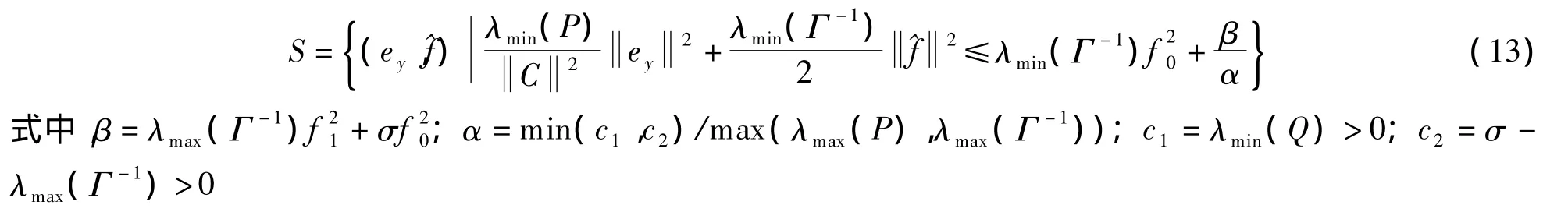
定理1表明,通过选择相关参数,能使需要的故障估计和状态估计值收敛到尽可能小的域内.但是由于故障估计的初始值一般选为0,一旦遇到故障值较大的情况,收敛时间会相对较长.因此,基于这种情况,需要提出一组故障诊断和容错控制机制及其切换律,以进一步提高故障估计的快速性和容错控制品质.
3 自适应故障切换与容错控制
引理1 对于任一常数μ>0和任一对称正定阵M,2uTMv≤uTMu/μ+μvTMv.
该引理为本文的证明提供理论依据.下面通过定义1和引理2给出ex和ef的关系.
定义1[8]一个系统x˙=f(x,u)被称作在[0,t)上对u输入状态实稳定(ISPS),如果存在β∈κl,α,γ∈κ∞以及一常数>0,使得对于任一有界输入u和初始状态x(0),都有时,称为输入状态稳定(ISS)[9].其中,κ为一系列单调递增的连续函数[0,∞)→[0,∞);κ∞为 κ 的一个子集,是无界函数的集合.如果 β∈κl,β:[0,∞)×[0,∞)→[0,∞),则对任意固定的 t≥0,β(·,t)∈κ;对任一固定的 s≥0,当 t→∞时 β(s,t)→0.
引理2 在假设1成立的条件下,故障诊断算法(6)~(8)能保证ex对ef输入状态稳定,即存在βe∈κl,αe,γe∈κ∞,使得
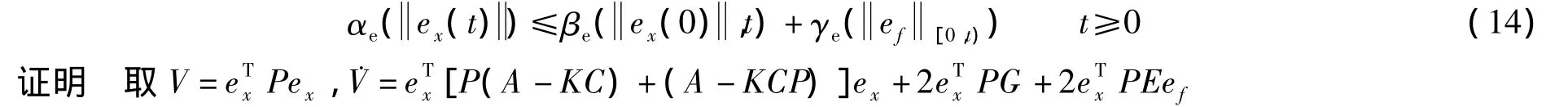
由引理1和Lipschitz条件可知
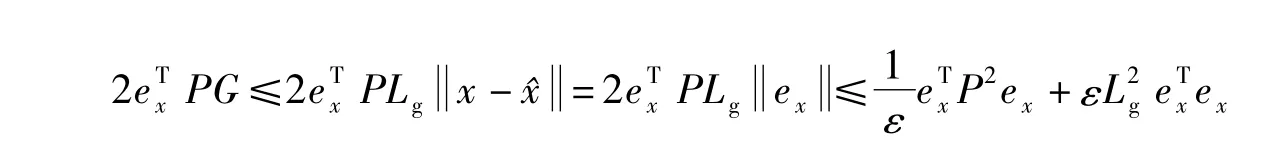
则当 ε1>0,且 -λmin(Q)+ε1<0时,有
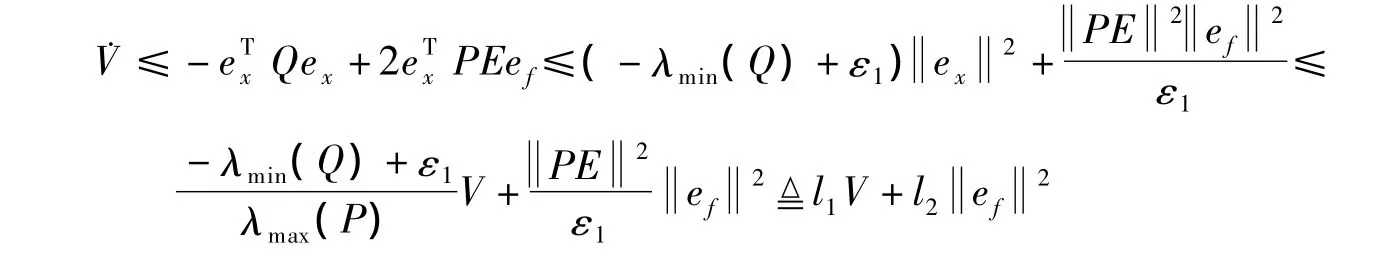
进而可得
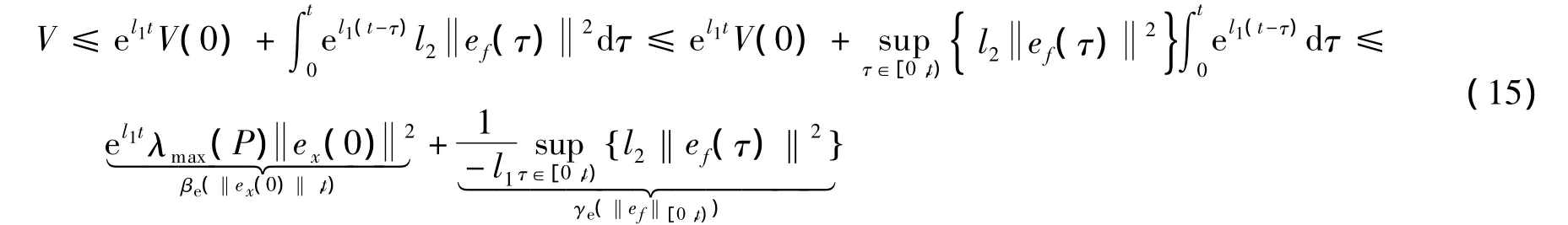
定义αe(·)=λmin(P)(·)2,则由式(15)可知,式(14)成立.证毕.引理2说明,如果切换系统初始状态误差ex(tj)固定,则由式(14)可得
由此可知,βe一定时,小的估计误差ef意味着小的状态误差ex,即通过减小ef可以提高故障估计的快速性.将故障的范围分成若干块,针对每一块,分别设计一个故障诊断机制,该机制的故障估计初始值选在该块内(见图1).当实际故障发生后,在故障估计初始值距离实际故障值最近的一组中,故障诊断机制可提供更小的ef,因此其估计速度比其他机制快.
下面,在给出具体的算法流程之前,先给出如下的观测器形式:

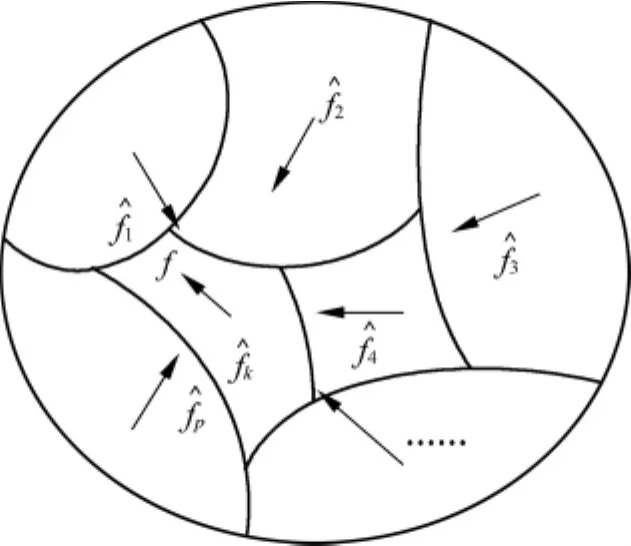
图1 故障范围分布图
详细的算法流程如下:
①设计多个自适应观测器,观测器状态初值相同,故障估计初值不同,如式(16)~(19)所示.
②令j=0.
③ 在tj=jΔT时(ΔT为一个切换周期),令Cexk=C(x-k).将得到的k*(t)与(t)作为附加控制律u的反馈参量,并且使切换时刻t+j时多个自适应观测器的初始状态误差ex(tj)相同,即k(tj)=k*(tj),k≠k*,k∈N.
由步骤③可知,该算法选择的是具有最小输出误差的观测器的估计值.这是因为在切换时刻各个子系统的状态误差保持一致,ex,ef能更快收敛(见图2).图2中有2个观测器,且只为更好说明,并非实际轨迹.
下面将具体叙述算法流程中附加控制律u的设计问题.
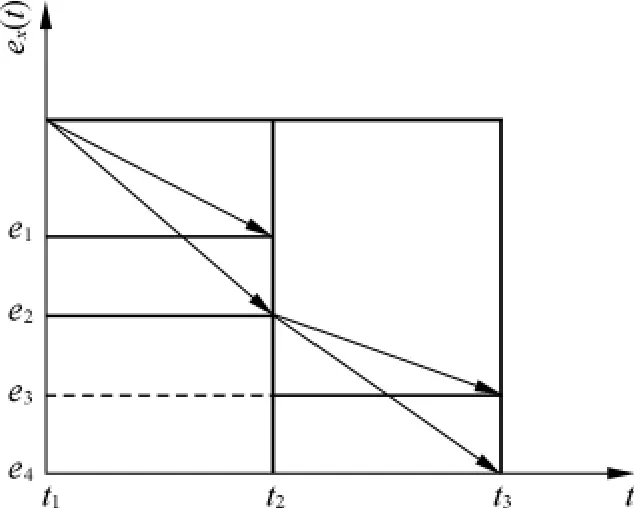
图2 状态误差变化趋势图
由于(A,B)可控,给定一正定对称阵W,求解得到一对称正定阵H,使下式成立:

假设2 对于系统(2),存在一对称正定阵H和一个连续有界函数η(x,t)>0,使得H是式(20)的解,且

假设3 rank(B,E)=rank(B),即等价于存在B*,使得(I-BB*)E=0.
由此可知,附加控制律设计为

引理 3[9]如果存在 α1,α2,α3,γ1∈κ∞,1>0和一光滑函数V:Rn→R≥0,使得
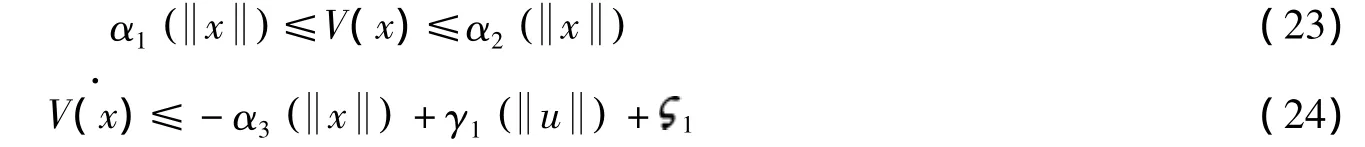
则系统x˙=f(x,u)在[0,t)上对u输入状态实稳定.
证明 将反馈控制律(22)代入式(2)中,得到如下的闭环动态方程:
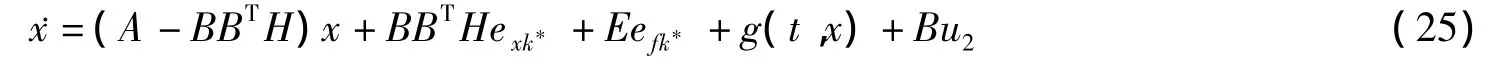
令 Φ =xTHx,则
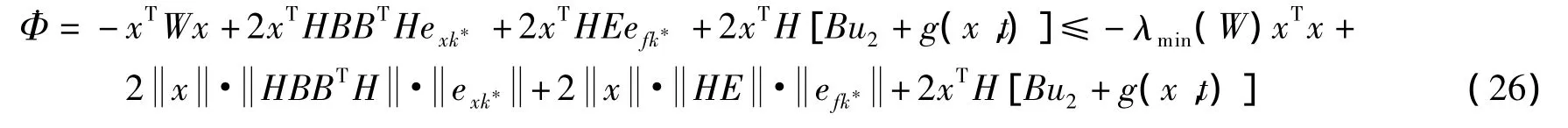
由式(21)和(22)得
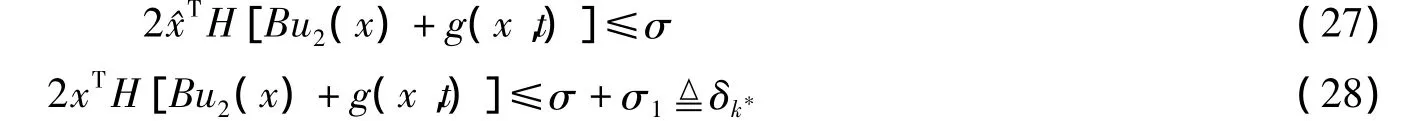
式中,σ1表示由x直接代替^x带来的微小误差.由此可见,假设2保证了u2连续且局部有界.另外由引理1可得
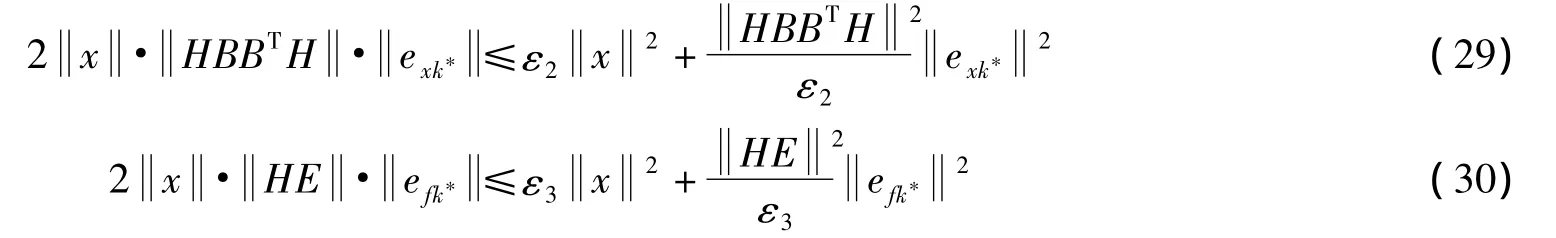
式中,ε2,ε3>0;-λmin(W)+ε2+ε3<0.
将式(28)~(30)代入式(26)中,可得
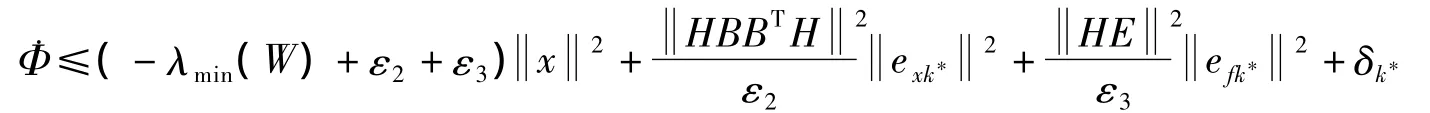
显然,由引理3可知,系统(2)在[t0,t)上对exk*,efk*和一常数k*>0输入状态实稳定.证毕.
综合考虑水功能区水质状况、当地技术经济条件和经济社会发展水平,以从严控制水功能区入河污染物总量为指导,按照以下原则确定水功能区限制排污总量。
4 仿真实例
引入一无人机纵向模型[10],取E=B,Q=W=I4,第1通道非线性项为 g1(t,x)= -9.780 7sinθ,其他通道为0.计算得到各参数阵如下:


选取2组自适应观测器进行仿真实验,其故障估计初值分别设置为0和1,且为了便于比较,学习率选择较小.诊断切换机制选择输出误差较小的观测器所产生的状态和故障估计值.图3为故障估计效果图,表示在3 s时发生了2个定值故障,大小分别为4和2.虚线是加切换系统后的估计曲线,实验表明比传统单一估计逼近更快.
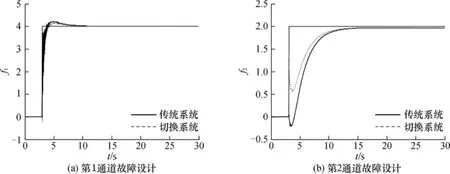
图3 故障估计效果图
图4是状态变量效果图,分别是4个状态变量的收敛情况,虚线是加入切换系统后的控制效果曲线,可见状态收敛比单一估计时更快.
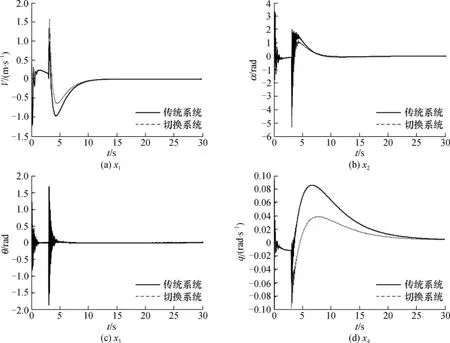
图4 状态变量效果图
5 结语
本文针对无人机非线性系统进行故障调节,并引入无人机纵向模型进行仿真验证.其关键在于故障估计的切换,即基于原先单个自适应故障估计算法,通过设置不同的故障估计初始值,再按输出误差最小原则选择最优估计值作为反馈量.仿真效果表明,故障估计逼近越快,状态收敛速度快.
References)
[1]Bateman F,Noura H,Ouladsine M.A fault tolerant control strategy for an unmanned aerial vehicle based on a sequential quadratic programming algorithm [C]//Proceedings of the 47th IEEE Conference on Decision and Control.Cancun,Mexico,2008:423-427.
[2]Bateman F,Noura H,Ouladsine M.Actuators fault diagnosis and tolerant control for an unmanned aerial vehicle[C]//Proceedings of the 16th IEEE International Conference on Control Applications.Singapore,2007:1061-1066.
[3]Cai G,Cai A K,Chen B M,et al.Construction,modeling and control of a mini autonomous UAV helicopter[C]//Proceedings of the IEEE International Conference on Automation and Logistics.Qingdao,China,2008:449-454.
[4]吴宝军.无人机飞行控制系统故障检测技术研究[D].西安:西北工业大学自动化学院,2007.
[5]Jiang B,Wang J,Soh Y C.An adaptive technique for robust diagnosis of faults with independent effects on system outputs[J].Int J control,2002,75(11):792-802.
[6]Rajamani R,Cho Y M.Existence and design of observers for nonlinear systems:relation to distance to unobservability[J].Int J Control,1998,69(5):717-731.
[7]Jiang B,Staroswiecki M,Cocquempot V.Fault accommodation for nonlinear dynamic systems[J].IEEE Transactions on Automatic Control,2006,51(9):1578-1583.
[8]Sontag E,Wang Y.New characterizations of input-to-state stability[J].IEEE Transactions on Automatic Control,1996,41(9):1283-1294.
[9]Sontag E,Wang Y.Characterizations of the input-to-state stability property[J].Systems and Control Letters,1995,24(5):351-359.
[10]荣辉,李冬,殷堂春.基于Matlab无人机数学模型仿真分析与研究[J].科学技术与工程,2008,8(6):1510-1514.Rong Hui,Li Dong,Yin Tangchun.Matlab simulation analysis and research based on UVA mathematical models[J].Science Technology and Engineering,2008,8(6):1510-1514.(in Chinese)
Switching fault diagnosis and accommodation for UAV based on multiple observers
Lu Lingli Jiang Bin Yang Hao
(College of Automation Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
A novel switching fault diagnosis and accommodation method for nonlinear unmanned aerial vehicle(UAV)models is proposed to improve the fault estimation and fault tolerant control performances.A set of fault diagnosis schemes are constructed with different initial fault estimation values and a switching law.The approach designs a set of adaptive fault estimation schemes based on the single adaptive fault estimation algorithm.The actual fault scope is divided into several parts,and a different initial fault estimation value for each fault zone is set.The switching law is constructed according to different performance requirements.Under the switching law,the convergence of the closed-loop system is ensured by choosing the state and fault estimation generated by the optimal diagnostic scheme according to the output error minimum principle,which is used in the fault tolerant controller design.The proposed method improves the estimation speed and the performance during the whole control process.The simulation results on a specific UAV model prove the effectiveness of the proposed method.
unmanned aerial vehicle;switchingfault diagnosis and accommodation;fault tolerant control
TB277
A
1001-0505(2010)增刊(I)-0048-07
2010-05-18. 作者简介:陆玲莉(1986—),女,硕士生;姜斌(联系人),男,博士,教授,博士生导师,binjiang@nuaa.edu.cn.
国家自然科学基金资助项目(60874051)、南京航空航天大学引进人才科研基金资助项目(S1012-031).

