线性代数在数学建模中的应用

李秀兰，张红玉

(山西大同大学数学与计算机科学学院，山西大同 037009）

线性代数在数学建模中的应用

李秀兰，张红玉

(山西大同大学数学与计算机科学学院，山西大同 037009）

通过在线性代数教学中的经验，阐述了线性代数教学中引入实际应用问题的重要性，并且通过具体例题给出了线性代数在数学建模中的应用.

线性代数 数学建模 应用

线性代数是高等院校理工科开设的一门主干课程，它具有较强的逻辑性、抽象性和广泛的实用性.但是传统教学中基本采用重概念，重计算的思路方法，这样，教学的结果只是让学生感觉到学习线性代数的抽象性、逻辑性，而没有体现出它的实用性，从而造成了学生学习线性代数的障碍和困难，以致于毕业后不懂得如何运用学过的数学知识去解决实际问题，甚至有人因此认为学数学无用.形成时代要求培养掌握和运用技术的新型人才与现行理工科数学教育脱离的矛盾.

钱学森前辈曾就数学教育改革问题指出：“理工科大学的数学课是不是要改造一番”，以“应付现在的实际”.我们现在处于21世纪，这是一个工程数学技术的时代，与我们所处的时代相适应，理工科数学教育应当包括如下三个方面的内容：基本知识的传授，自学能力锻炼，应用数学知识解决实际问题能力的培养.目前国内外高等院校纷纷开展“数学建模与数学模型”教学，这已经成为数学教育改革的一大热点.

数学建模是对实际问题进行分析，建立数学模型，对模型求解并用于实际问题的处理，它可以训练学生观察问题、分析问题以及综合运用数学知识解决实际问题的能力.姜启源说，建立数学模型来解决实际问题，是学生在走上工作岗位后常常要做的工作.做这样的事情，所需要的远不只是数学知识和解数学题的能力，而需要多方面的综合知识和能力.社会对具有这种能力的人的需求，比对数学专门人才的需求要多得多.下面通过具体实例来体会应用型问题对线性代数学习的帮助.

例1给出四个城市A、B、C、D，现在想作一次旅游，方式为：先坐火车后坐汽车.即从第一个城市坐火车到第二个城市，然后从第二个城市坐汽车到第三个城市.那么在哪两个城市之间才能作一次使用两种交通工具(先坐火车后坐汽车)的旅行？四个城市之间的火车交通线路情况如图1所示；汽车交通线路情况如图2所示；反映火车和汽车的交通线路情况如图3所示.

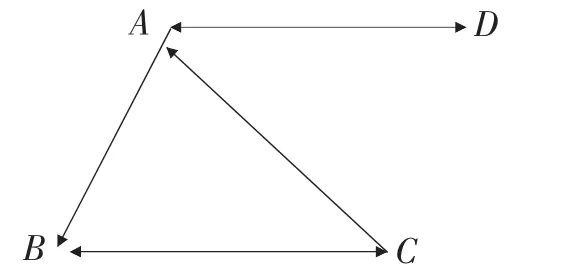
图1 火车交通路线

图2 汽车交通路线

分析：火车交通线路情况、汽车交通线路情况可以用矩阵S，T来描述：

代表坐火车可以从哪个城市到哪个城市

代表坐汽车可以从哪个城市到哪个城市.

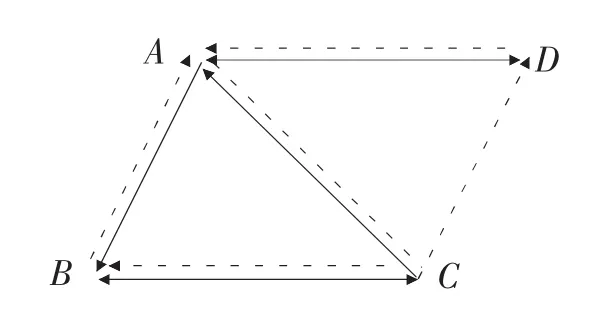
图3 火车和汽车交通路线

从图3可以看出，可以先坐火车从A到B或到D.从B可以坐汽车回到A，从D也可以坐汽车回到A，所以从A到A可以作两次旅行 (先坐火车后坐汽车)，但有两种不同的路线.从A到其它任何城市都不能作这种旅行.如果从B可以坐火车到C，然后坐汽车回到B，当然也可以去A或D.因此，从B到A、B、D都可以先坐火车后坐汽车.其实根据图3，先坐火车后坐汽车从一个城市到另一城市的旅游可以用矩阵P来描述，

可以发现P就是S，T的乘积,P的第i行第j列的元素表示先坐火车后坐汽车从i城市到j城市的路线数.

这就是矩阵乘积的一个应用，也是建模思想的融入.在类似例题的引导下，教师能够很容易地引出矩阵的概念、矩阵的乘法，学生掌握起来也很轻松.

例2假定某地人口总数保持不变，每年有5%的农村人口流入城镇，有1%的城镇人口流入农村.问该地的城镇人口与农村人口的分布最终是否会趋于一个“稳定状态”.

解设该地人口总数为m，从今年开始，第i年该地的城镇人口数与农村人口数分别为xi与yi，依题意有则αi＋1＝Aαi，经计算可得A的特征值为1和0.94，它们对应的特征向量分别为ξ1＝解关于k1，k2的方程

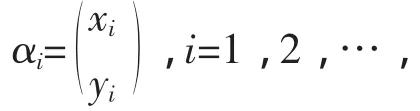
因此，最终该地的城镇人口与农村人口的分布最终会趋于一个“稳定状态”.即城镇人口约占总人口的，农村人口约占总人口的

这个问题利用特征值和特征向量理论，讨论了该地的城镇人口与农村人口的分布最终会趋于一个“稳定状态”.

总之，我们在线性代数的教学中，要注重引入实际问题，一方面能培养学生解决实际问题的能力，另一方面能激发同学们对学习这门课程的兴趣，因此在线性代数的教学中，一定要注意多引入实际问题.

[1]姜启源.数学实验与数学建模[J].数学的实践与认识，2001，31(5)：613-617.

[2]李尚志.培养学生创新素质的探索——从数学建模到数学实验[J].大学数学，2003，19(1)：46-50.

[3]同济大学应用数学系.线性代数及其应用[M].北京：高等教育出版社,2004.

[4]谌跃中.探讨线性代数的核心[J].数学理论与应用，2005，25(4)：145-147.

［5］张红玉.污染线性模型的矩估计［J］.山西大同大学学报：自然科学版，2009，25（5）：13－15.

Applications of Linear Algebra in M athematical M odeling

LIXiu－lan，ZHANG Hong－yu
(School of Mathematics and Computer Science,Shan x i Da t ong University,Da t ong Shan x i，037009)

Teaching of Linear Algebra by author＇s experience，described the introduction of linear algebra teaching the importance of practical application，and specifically example of linear algebra is given in the application ofmathematicalmodeling.

linear algebra；mathematicalmodeling；application

O151.2

A

〔编辑 高海〕

1674-0874(2010)02-0003-02

2009-12-15

山西省教育科学“十一五”规划课题项目 [GH-09090]；我国高校应用型人才培养模式研究数学类子课题 [FIB-070335-A2-22]；山西大同大学青年科学研究项目[2009Q2]

李秀兰(1966-)，女，山西大同人，硕士，教授，研究方向：图论.