时间模上非线性两-点边值问题的正解

乔世东，张 英

(山西大同大学数学与计算机科学学院，山西大同 037009）

时间模上非线性两-点边值问题的正解

乔世东，张 英

(山西大同大学数学与计算机科学学院，山西大同 037009）

变系数模型是由古典的线性模型发展而来，它们可以很好地检验函数系数随着协变量的变化程度.文章用PLR提出了变系数模型误差方差的估计，并研究了它的渐近正态性，进一步用一个模拟例子来说明估计的结果是有效的.

正解 时间模 边值问题 Leray-Schauder原理 障碍带

最近几年，时间模上的动力学方程的研究发展很快，因为它的研究在自然界有重要的应用，许多学者研究时间模上的边值问题正解的存在性.本文讨论二阶非线性两-点边值问题的正解.

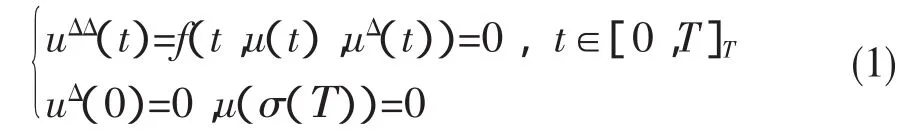
引理[1]设X，Z是实向量赋范空间，L∶domL⊂X→Z是一个指标为零的线性Fredholm映射，Ω⊂X是一个有界开子集，N∶Ω→Z是一个L紧映射.如果ker f＝{0}，0∈Ω，且Lu-λNu≠0，对于每一个（u，λ）∈（domL∩∂Ω）×（0，1），则方程 Lu＝Nu在domL∩里至少有一个解.

定理1[2]设f∶［0，σ（T）］×R2→R连续，L∶P∩E→Crd［0，T］为一一映射，若存在常数r＜∞，使得对边值问题：

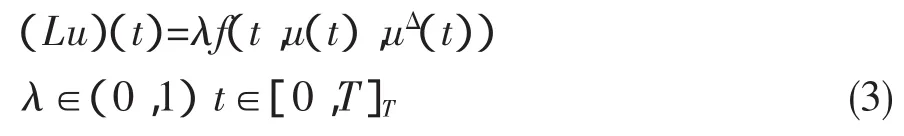
的任一个解u（t），有‖u‖＜r，则边值问题(1)在P中至少有一个解.

定理2设f∶［0，σ（T）］×R2→R连续，若存在常数Li，i＝1，2，3，4，使得L2＞L1≥0，L3＜L4≤0，若f满足：及

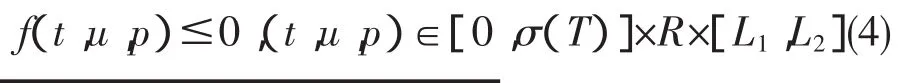
f（t，u，p）≥0，（t，u，p）∈［0，σ（T）］×R×［L3，L4］(5)则边值问题(1)在P中至少有一个解.

证明 定义映射Φ∶R→R满足如下条件：

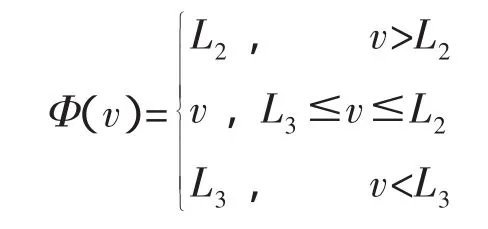
考虑下面的边值问题

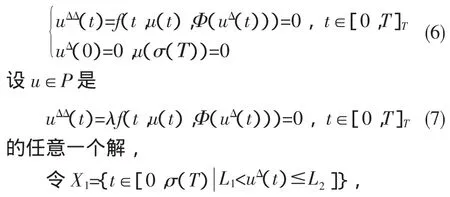
则 X1＝φ.

反证，设存在t0∈X1，使得u△（t0）＞L1，令A＝｛t∈［0，σ（t0）］＜u（△t）≤L2｝，因为0∈A，所以，A≠φ.选取t1＝sup A，则t1∈A.事实上，若t1∉A，则u（△t）1＞L1，下面先讨论t1右边的情况.当σ（t）1＝t1，有u△（t1）≥L1，t∈［t1，t0］，因此，L1＜Φ（u△（t））≤L2，t∈［t1，t0］，所以

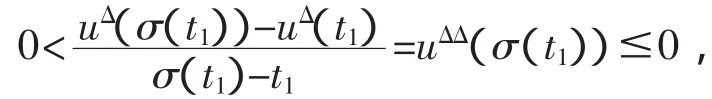
令X2＝｛t∈［0，σ（T）＜u（△t）≤L4］｝，类似的证明知 X2＝φ.

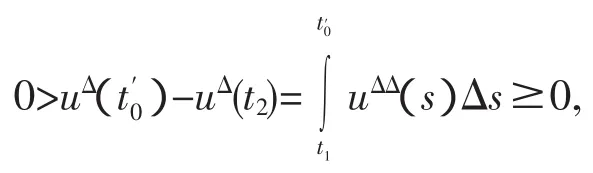
[1]Mawhin J.Topological degree and Boundary Value Problem for nonlinear Differential Equations[J].Math.Soc.Providence，1979,29: 1258-1264.

[2]马如云.非线性微分方程非局部问题[M].北京：科学出版社，2004.

[3]葛胃高.非线性常微分方程边值问题[M].北京：科学出版社，2007.

[4]Ruyun Ma，Hua Luo.Existence of Solutions for a two-point Boundary Value Problems on time scales[J].JAppl Math Comput, 2004，150：139-147.

Positive Solutions For Nonlinear Two-point Boundary Value Problems on Time Scales

QIAO Shi-dong，ZHANG Ying
(School ofMathematics and Computer Science，ShanxiDatong University，Datong Shanxi，037009)

In this paper，we study the existence of at least one positive solutions of a nonlinear second-order two-point boundary value problem for dynamic equations on time scales.Our tools are the Leray-Shauder principle and an existence assumption of barrier stripswithout any growth restrictions of f.

positive solution；time scales；boundary value problem；leray-Shauder principle；barrier strips

O175.14

A

〔编辑 高海〕

1674-0874(2010)02-0001-02

2009-12-25

山西省高校科技研究开发项目[200811043]

乔世东(1963-)，男，山西左云人，硕士，教授,研究方向：常微分方程.