一类非线性差分方程的平衡解及解的渐近性和有界性
明亚东,安存斌
(山西大同大学数学与计算机科学学院,山西大同 037009)
一类非线性差分方程的平衡解及解的渐近性和有界性
明亚东,安存斌
(山西大同大学数学与计算机科学学院,山西大同 037009)
研究了一类非线性差分方程的平衡解与解的渐近性和有界性,利用差分不等式得到解的渐近性的一些充分条件,利用归纳法证明了方程的解是有界的.
差分方程 平衡解 渐近性 有界性
差分方程的振动性和非振动解的渐近性是差分方程定性理论的重要组成部分,这方面的理论从很早开始就受到国内外众多学者的重视,已有很多研究结果,文献[1]和[2]系统地介绍了这方面的基本理论.
讨论方程

的平衡解及解的渐近性、有界性.相应的初始条件为

1 方程的平衡解
我们看到Pn=0是方程(1)的解,而Pn=P是方程(1)的正平衡解的充分必要条件是

2 方程的解的渐近性




因此,pn在[0,∞)内单调不增.
(I)当p0∈(0,ω)时,
0<pn≤p0<ω,n=1,2,…,从而由g(x)的单调性,有

仿定理1的证明可得
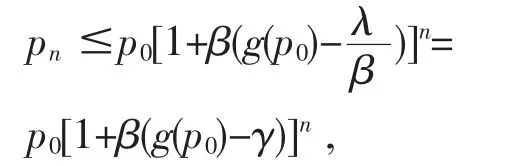
由于0<1+β(g(p0)-γ)<1,因此当n→∞时,pn→0.故(4)成立.
(II)当当p0∈(ω,+∞)时,且对任意x>ω时(6)成立,则必然有
pn>ω,n=1,2,….
事实上,

设F(x)=(1-γ)x+βf(x),(x>ω),
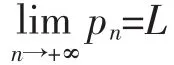


3 方程的解的有界性
定理4假设(3)成立,则初值问题(1)及(2)存在唯一正解pn,并且pn有界.
证明 考虑(2),(3)和

归纳法得pn≤M,n=0,1,2,….证毕.
[1]王联,王慕秋.常差分方程[M].乌鲁木齐:新疆大学出版社,1991.
[2]张广,高英.差分方程的振动理论[M].北京:北京教育出版社,2001.
[3]Saker SH.Permanence,oscillation and attractivity of the discretehematopoiesis,modelwith variable coefficients[J].Nonlinear Analysis, 2007,67:2955-2965.
[4]SakerSH.Oscillationand globalattractivityinhematopoiesismodelwithdelay time[J].AppliedMathermaticsand Computation,2003,136: 241-250.
Steady Solutions Asymptotic Behavior and Bounded Behavior for A Nonlinear Difference Equation
Ming Ya-dong,An Cun-bin
(School of Mathematics and Computer Science,ShanxiDatong University,Datong Shanxi,037009)
In this paper,steady solutions and asymptotic behavior and bound behavior of solutions for a nonlinear difference equation are studied,the sufficient conditions for asymptotic behavior of solutions are acquired with difference inequations,and we demonstrate thatevery solutions of the equation is bounded by induction..
difference equation;steady solution;asymptotic behavior;bound behavior
O151.22
A
〔编辑 高海〕
1 6 7 4-0 8 7 4(2 0 1 0)0 4-0 0 0 3-0 3
2 0 1 0-0 5-0 2
明亚东(1 9 6 6-),女,辽宁绥中人,硕士,副教授,研究方向:微分方程.

