含负折射率介质层的一维光子晶体缺陷模的特性

董海霞，杨成全，石云龙

(1.山西大同大学物理与电子科学学院，山西大同 037009; 2.山西大同大学固体物理研究所，山西大同 037009)

含负折射率介质层的一维光子晶体缺陷模的特性

董海霞1，杨成全1，石云龙2

(1.山西大同大学物理与电子科学学院，山西大同 037009; 2.山西大同大学固体物理研究所，山西大同 037009)

利用转移矩阵给出了在正常材料中加入双负介质结构的色散关系和缺陷模的本征频率方程.根据本征方程计算了当缺陷层的折射率和光学厚度改变时缺陷模频率的变化.

光子晶体 负折射率材料 缺陷模

光子晶体是由不同折射率的材料在空间按一定周期排列组成的一种晶体结构.由于它具有全新的控制光子传播的机制，所以一被提出来就得到了广泛的关注[1-3].制备光子晶体的材料除了正常材料和单负性材料之外，还有双负性材料.双负性材料，是介电常数ε和磁导率μ均为负的材料.因其折射率为n=-(εμ)1/2，故又称负折射率材料.含有负折射率材料的光子晶体具有很多特性[4].在正常材料中加入双负性介质后出现了缺陷模，中山大学[5]利用公式形象地说明了在介质折射率变化时缺陷模的变化.本文用转移矩阵方法给出了在正常材料组成的一维光子晶体中加入双负性介质后，在能隙中出现的缺陷模的本征频率方程，并且研究了缺陷模的一些基本特性.

1 结构的能带与缺陷模频率

图1 含双负性材料的一维光子晶体结构图

图1是一个ABAB…ACA…BABA排列的一维光子晶体的结构示意图.

图中A，B代表正折射率(非磁性)材料，介质C代表负折射率材料，并且假设所有材料都是均匀且各向同性的.材料层的折射率和厚度分别为nA,nB, nC和 dA,dB,dC.

设电磁波以入射角θ从空气中射入该结构.入射电磁波的波矢k位于xoz平面.这里只考虑电场方向位于y方向的横电(TE)波.对于由A,B两种正折射率材料组成的一维光子晶体来说，位于z+Δz和z处的电场分量和磁场分量通过以下转移矩阵相连接：

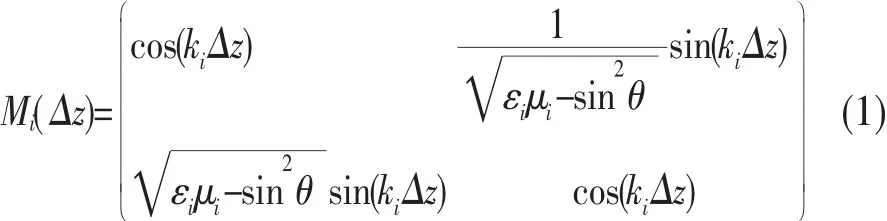
其中,ki=ω(εiμi-sin2θ)1/2/c，i=A，B，c为真空中的光速.对无限周期结构，它的色散方程为：

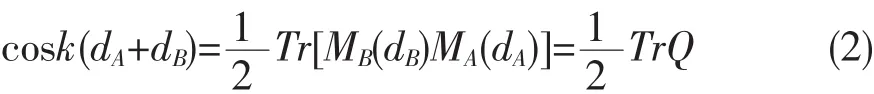
光波中凡|TrQ|<2的频率给出允许带，在其中波数k为实数，光波是可以传播的；满足|TrQ|>2的频率给出禁带，在其中k为虚数，光波是不可以传播的.假设连接入射端电磁场和出射端电磁场的矩阵为XN(ω)，经过计算，可得出此结构的透射系数：

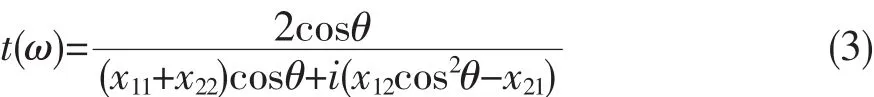
其中,xij(i，j=1，2)为XN(ω)的矩阵元，结构的透射率则为|t(ω)|2.

对完整光子晶体，其色散方程为方程(2).在由A，B组成的完整光子晶体中加入一个缺陷层C，由于完整周期性的破坏，在光子能隙中将出现局域化的缺陷模.含缺陷的光子晶体可看成是两边为半无限的周期性晶格通过缺陷耦合在一起的结构.跨越缺陷的电场和磁场分量通过以下矩阵连接：

其中，kc=ncω/c为缺陷中的波数.对局域化的缺陷模，在缺陷两边半无限周期区域中的电磁场为迅衰场，这两个迅衰场在缺陷处相互连接在一起.利用方程(2)和方程(4)，就可得到缺陷模频率的本征方程[6]：

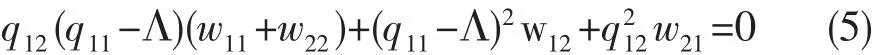
其中qij,wij(i，j=1，2)分别为方程(2)和(4)中的Q与W的矩阵元.并且

2 加单层杂质时缺陷模的特性

在光子晶体中加入一层缺陷C，正入射情况时，固定A、B、C的厚度，研究缺陷模的频率随缺陷层折射率nC的变化关系.在数值计算中只选取了5个主周期数，材料的折射率分别为nA=4.6，nB= 1.6，光学厚度为 nAdA=nBdB=0.25λ0，nCdC=-0.5λ0，这里λ0是一预先给定的光波长，相应的频率ω0位于禁带中心.

图2是结构在nC=-2.8时的透射谱[5].从透射谱中可以观察到带隙中出现三个缺陷模，其中一个位于带隙中心，另外两个分别位于中心两侧.

图2 结构的透射谱

处于两侧的这两个缺陷模的频率随|nC|变化而变化，变化规律如图3所示.从图中可以看出，当|nC|为2.2左右时，两个缺陷模已分别从左右两带边出现.随着|nC|的增加，左边缺陷模的频率在能隙中呈上升趋势，逐步向中间的缺陷模靠拢.同时右边缺陷模的频率呈下降趋势，也向中间的缺陷模靠拢.两个缺陷模最终与中间的缺陷模重合在一起.二者频率变化的速度一致，都随着|nC|的增大而增大.

图3 缺陷模的频率随|nC|的变化

若双负性材料C的光学厚度nCdC=-0.25λ0时，带隙中只会出现一个缺陷模.图4是该缺陷模的透射率随着缺陷层的折射率绝对值｜nC｜变化的规律图.可以发现，这个缺陷模的透射率在开始时随着杂质折射率|nC|的增大变化较缓慢，当|nC|超过1.4后，几乎成线性减小.

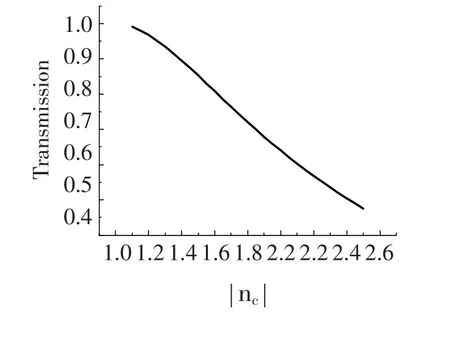
图4 缺陷模的透射率随|nC|的变化

3 加两层杂质时缺陷模的特性

若在上述的一维光子晶体结构中再加入一层双负介质D，看看缺陷模的透射率是怎样变化的.选取D的折射率nD=-2，C的折射率nC=-1.5.当保持nCdC+nDdD=-0.5λ0，同时改变dC和dD，缺陷模的频率就会随｜nDdD｜的变化而变化，变化结果如图5所示.从图中可以看出缺陷模的频率会随杂质D的光学厚度的变化成一定的规律.当｜nDdD｜变化时，缺陷模的频率会在中心频率1的附近做往复变化.

4 结论

光子晶体存在光子带隙，在光子晶体中引入缺陷后就会在带隙中出现缺陷模.利用光子晶体的带隙和缺陷模可以方便地控制光子的传播.利用转移矩阵可以得出缺陷模的本征频率方程.从数值计算的结果可看出缺陷模的频率、透射率等特性都可以通过改变缺陷层的光学厚度、折射率以及缺陷层的位置等来调节.在由正常材料A、B组成的一维光子晶体中加入双负性缺陷层后，通过选择适当的参数，就会出现缺陷模.若缺陷层材料的折射率或它的光学厚度改变时，缺陷模的频率就会发生变化.通过这些关系可以为设计并制造各种特性的光学器件提供重要的参考依据.

图5 缺陷模的频率随｜nDdD｜的变化

[1]Yablonovitch E.Inhibited spontaneous emission in solid-state physics and electronics[J].Phys Rev Lett,1987,58:2059-2062.

[2]王辉,李永平.用特征矩阵法计算光子晶体的带隙结构[J].物理学报,2001,50(11):2172-2178.

[3]杜桂强,刘念华.具有镜像对称结构的一维光子晶体的透射谱[J].物理学报,2004,53(4):1095-1097.

[4]董海霞,杨成全,石云龙.含负折射率材料的一维光子晶体掺杂后的滤波特性[J].光电子·激光,2007,18(12):1435-1437.

[5]Haitao Jiang,Hong Chen,Hongqiang Li,et al.Omnidirectional gap and defect mode of one-dimensional photonic crystals containing negative-index materials[J].Appl Phys Lett,2003,83(26):5386-5388.

[6]Kun-yuan Xu,Xiguang Zheng.Properties of defect modes in one-dimensional photonic crystals containing a defect layer with a negative refractive index[J].Appl Phys lett，2004,85(25):6089-6091.

[7]Nian-hua Liu.Defect Modes of Stratified Media[J].Phys Rev B，1997,55(7):4097-4100.

Abstract:By using transfer matrix method,the dispersion relations of a one-dimensional photonic crystal structure containing defect layers with negative refractive index and eigen equation of the defect mode are studied.It is found that when the refractive index of defects or optical thickness is changed,the frequency of the defect modes is varied.

Key words:photonic crystal;negative refraction materials;defect mode

〔编辑 李海〕

Properties of Defect Modes in One-dimensional Photonic Crystal Containing Defect Layers with Negative Refractive Index

DONG Hai-xia1,YANG Cheng-quan1,SHI Yun-long2
(1.School of Physics and Electronic Science,Shanxi Datong University，Datong Shanxi,037009; 2.Institute of Solid Physics,Shanxi Datong University,Datong Shanxi,037009)

O431

A

1674-0874(2010)04-0020-03

2010-05-20

董海霞(1977-)，女，山西大同人，硕士，讲师，研究方向：凝聚态物理.