差动驱动机器人的一种航迹推算定位方法

张 利, 潘承毅, 刘征宇, 徐 娟, 黄业伟

(1.合肥工业大学 机械与汽车工程学院,安徽 合肥 230009;2.合肥工业大学 计算机与信息学院,安徽 合肥 230009)

0 引 言

移动机器人导航的关键问题是定位,在解决定位问题中遇到的不确定性问题的方法各有优缺点[1]。基于接收信号强度、红外、蓝牙、超宽带等定位技术都是基于到达时间 TOA、到达时间差TDOA和到达方向AOA这类信息,这些技术的定位结果只有在通视信号占支配地位的情况下才是可靠的[2]。辅助定位就是为了弥补这些技术不足而提出来的,移动机器人的辅助定位技术主要有惯性定位、航迹推算定位。辅助定位具有短时间内局部高精度定位特点,结合常规定位[3],就能比较好地解决文献[2]中的室内非视距定位误差大的问题。从成本和实现的角度看,服务机器人的辅助定位一般采用航迹推算实现。

基于双轮差动驱动的航迹推算方法是建立其运动学微分方程[4],然后对方程进行数值积分迭代推算[4-9](简称为积分推算),从而实现对机器人的跟踪和定位。

积分推算的实质是用一小段直线代替机器人的一小段轨迹,在采样频率和采样精度有限下积分推算误差较大。为了进一步提高推算精度,本文从几何和运动学的角度提出用小段的圆弧来逼近轮椅实际行走的轨迹,在采样数据和采样精度不变下能有效地提高推算定位的精度。为了方便叙述,以下称该方法为几何推算方法。

1 几何推算方法原理

双轮差动驱动机器人转向的原理是：同轴的左、右2个主动轮转动角速度不同,当左轮转速nL大于右轮转速nR时,机器人就开始向右转;当nL＜nR时,机器人就开始向左转;当左右转速相同时则往正前方运动,2个驱动轮的运动轨迹满足同心圆的规律[4,7]。几何推算和积分推算都建立在这个原理上,积分推算用直线代替实际的曲线,如图1所示,Pi为 A、B轮轴线中点,o′为A 、B轮转弯时的转向圆心,积分推算方法用直线来逼近实际路线PiPi+1。

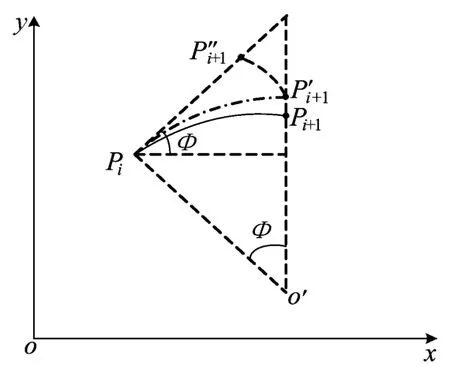
图1 微分和几何推算原理对比

几何推算法采用圆弧PiP′i+1来代替直线实际机器人运动的时候,其轨迹是由很多不同半径不同圆心的小段圆弧组成。显然,圆弧线PiP′i+1更加接近曲线 PiPi+1。因此,采用圆弧段代替行走的曲线段来推算机器人轨迹更加符合实际。图2所示为在速度测量无误差下行走圆弧路线积分推算和几何推算的定位结果对比。

图2 测量无误差沿圆弧行走定位对比

2 几何推算法推算过程

几何推算法推算下一个时刻的位置,需要知道当前左、右轮的位置及其对应的角速度。通过角速度ωL和ωR求出机器人的转向半径rm[4-7]和转向圆心o′点,采样时间 Ti内可以近似 ωL和 ωR的值不变,利用几何关系就可以求出下一个时刻左、右轮的位置。记左轮为 A,右轮为B,确定基于圆弧代替曲线的几何推算定位过程。

由圆周运动公式可知：

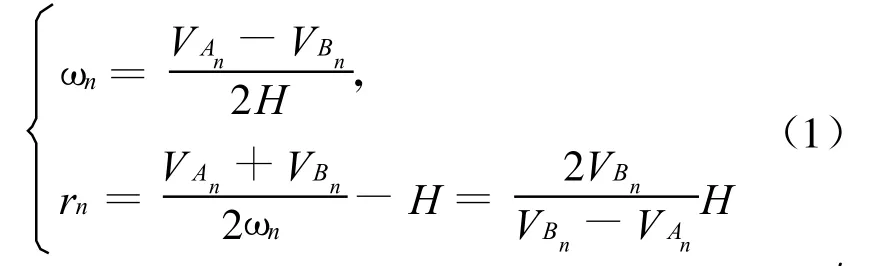
其中,rn是Tn时刻对应转向半径,即转向圆心o′到A轮的距离;H为轮子A、B间距的1/2。设Tn时刻转向圆心 o′坐标为o′(xo,yo),由于o′点在A、B轮的轴线上,o′到 A轮的距离为rn,即可以解出转向圆心o′(xo,yo)点的坐标值。

平移坐标系原点o(0,0)到转向圆心o′(xo,yo),此时的坐标系记为 o′-x′y′,并求出在 o′-x′y′坐标系下的An(xAn,yAn)、Bn(xBn,yBn)的坐标A′n(x′An,y′An)、B′n(x′Bn,y′Bn)。

将o′-x′y′坐标系旋转 θ角度,使得 o′-x′y′坐标系的x′轴与A、B轮子的轴线重合;旋转后的坐标系统记为o″-x″y″,其上点坐标记为(x″,y″)。其中θ值由(2)式确定：

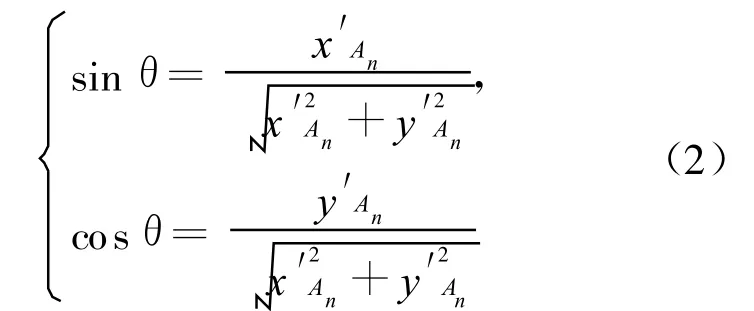
求出 A′n(x′An,y′An)、B′n(x′Bn,y′Bn)在 o″-x″y″下的坐标 A″n(x″An,y″An)和 B″n(x″Bn,y″Bn)。其中坐标变换矩阵C为：

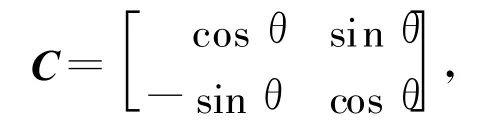
于是有：

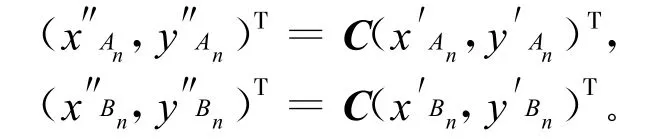
在采样时间 T内视ωn不变,则在这段时间内 A、B点相对于o′转的角度ω=ωnT,于是求出Tn+1时刻 A 和 B 在 o″-x″y″坐标系下的坐标(x″An+1,y″An+1)和 (x″Bn+1,y″Bn+1)。

通过坐标线性变换,可得到A在Tn+1时刻的 坐标An+1(xAn+1,yAn+1)为：

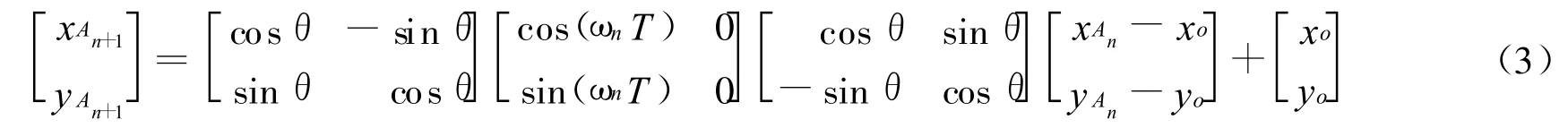
同理,求出点B在Tn+1时刻坐标Bn+1(xBn+1,yBn+1)为：

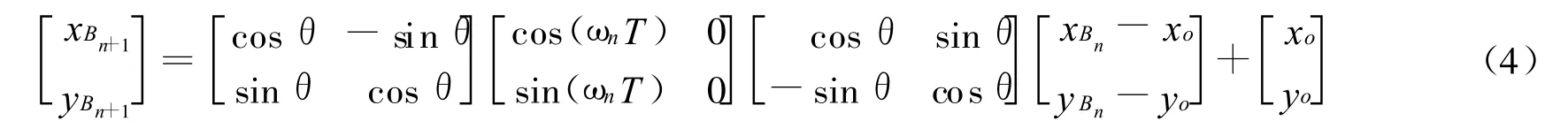
在已知A、B轮初始位置情况下,通过不断采样测量A、B的角速度ωA和ωB,将角速度乘以轮子半径R即可得两轮的线速度vAn、vBn,通过(1)式和圆周运动几何关系,可以求出xo和yo,代入(3)式和(4)式迭代计算,就可以逐步地推算出 A、B轮运动轨迹,从而实现对机器人定位。

3 仿真实验

3.1 计算机仿真验证原理

仿真实验首先要正确地获取2种数据,即机器人真实的行走轨迹、采样时刻A、B轮子的线速度。然后把A、B的各个采样点的角速度值ωA、ωB和转向圆心坐标(xo,yo)代人(3)式、(4)式,通过迭代计算即可推算出A、B轮的轨迹,再将推算的轨迹与理论拟定的轨迹进行比较。

3.2 仿真方法和数据vAn、vBn的获得

机器人实际行走轨迹是一个很复杂的模型,为了简化计算,同时又能验证本文阐述方法的可行性,本文设定机器人的中心D沿着特定的几种曲线运动,方法如下：

(1)拟定行走曲线y=f(x),其中f(x)为光滑曲线。

(2)将y=f(x)化为参数方程 x=x(t)和y=y(t)。

(3)求出行走路线 x、y轴方向上的速度分量,其中 vx=x′(t),vy=y′(t)。

(4)通过曲线y=f(x)求出其曲率半径,即相对于转向圆心 o′的转弯半径r,于是 ωn=,从而求出机器人 A、B轮在Tn时刻采样的精确线速度值vAn、vBn。

(5)将轮子线速度值vAn、vBn化为A、B轮的角速度值ωA、ωB,然后加上一个随机误差值error作为仿真测量值。

(6)将仿真测量值代入(3)式和(4)式,分别推算出A、B轮的轨迹,然后将拟定的轨迹与仿真计算出的轨迹进行对比和分析。

3.3 仿真实验的计算机环境

本文的仿真实验是在Windows操作系统上的VC++和Matlab上进行的,将3.2的几何推算步骤和积分推算方法转化为C++代码并在VC++上进行编译。

仿真时用同一份模拟测量数据(准确值+随机误差值)分别输入几何推算仿真程序和积分推算仿真程序,并将2种推算的数据保存在text文件中,然后把text文件的数据导入Matlab进行绘图和比较分析。

3.4 仿真推算轨迹与理论拟定轨迹对比

为了让仿真实验行走的路线有代表性,本文选择了圆弧、椭圆弧和sin x曲线段进行轨迹跟踪仿真。按照3.2的方法,分别对3种曲线仿真。

(1)沿着圆弧曲线行走的仿真。圆弧是差动驱动机器人最常见的行走轨迹,对沿圆弧行走定位的精度直接影响该推算方法是否有应用价值。本文阐述的几何推算法是基于机器人行走轨迹的圆弧段组成的理论,因此,理论上在没有速度测量误差的情况下沿着圆弧行走,几何推算的航迹与实际行走的轨迹应保持一致。图2为采样无误差、采样步数n=20时,轮椅沿着半径为40的半圆行走时,几何推算和积分推算轨迹对比图。显然,几何推算与理论拟定路线基本吻合,而积分推算产生了5%～12.5%的误差。

将真值加上一个5%随机误差,则可以视为测量值,仿真结果如图3a所示。

在采样精度不变的情况下,增加采样频率,能有效地降低定位误差。图3b所示是测量随机误差为5%,采样步数分别为200和2000时的几何推算仿真结果。

(2)沿着半椭圆曲线行走仿真。机器人沿着圆弧运动比较常见,图3证明几何推算法能跟踪机器人行走圆心固定的圆弧,但实际运动中机器人是行走不同圆心不同曲率的小段圆弧组成的曲线。椭圆曲线各点的曲率和曲心都不同,正好能验证这种情况。图4a所示是采样步数n=20,测量随机误差为5%时几何推算和积分推算2种方法的对比,图4b所示是采样步数n=400,测量随机误差为5%时的几何推算轨迹。

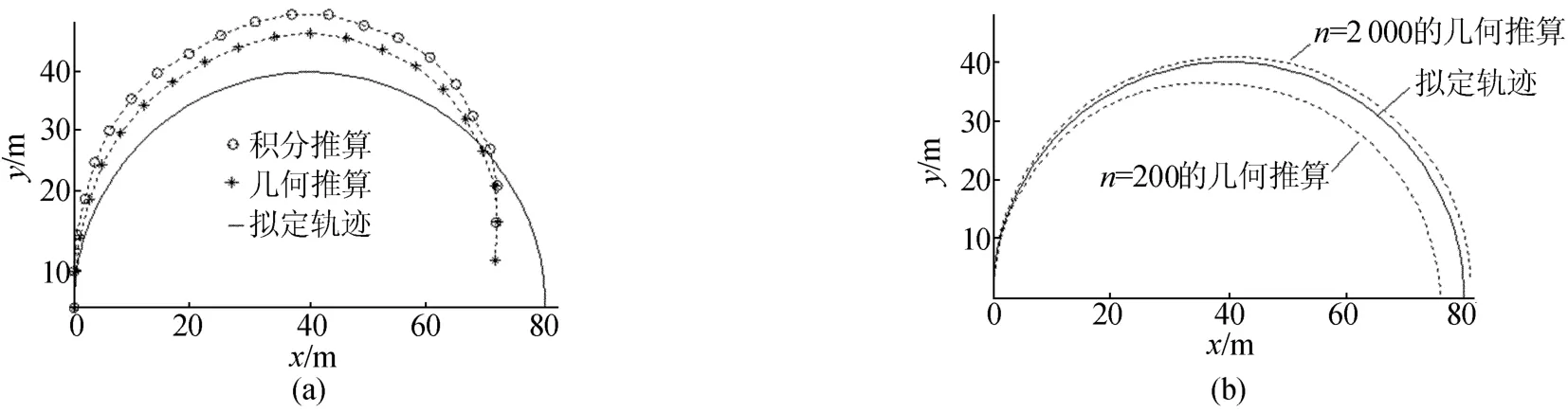
图3 测量误差为5%,沿着圆弧行走仿真

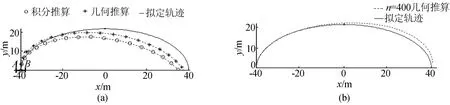
图4 测量误差为5%,沿着椭圆弧行走仿真

(3)沿着正弦曲线sin x行走的仿真。针对很复杂的运动模式,如速度、加速度、转向角速度都不断变化(实际很少甚至不可能出现),研究几何推算法是否有效。针对这种情况,本文拟定机器人沿着sin x曲线运动,机器人中心D点的速度在x轴上的分量恒为1个速度单位。由几何关系可知D点的速度、加速度和转向角速度都在不断变化。在采样误差为5%内,n=20时几何推算和积分推算仿真结果如图5a所示,n=50时几何推算的结果如图5b所示。

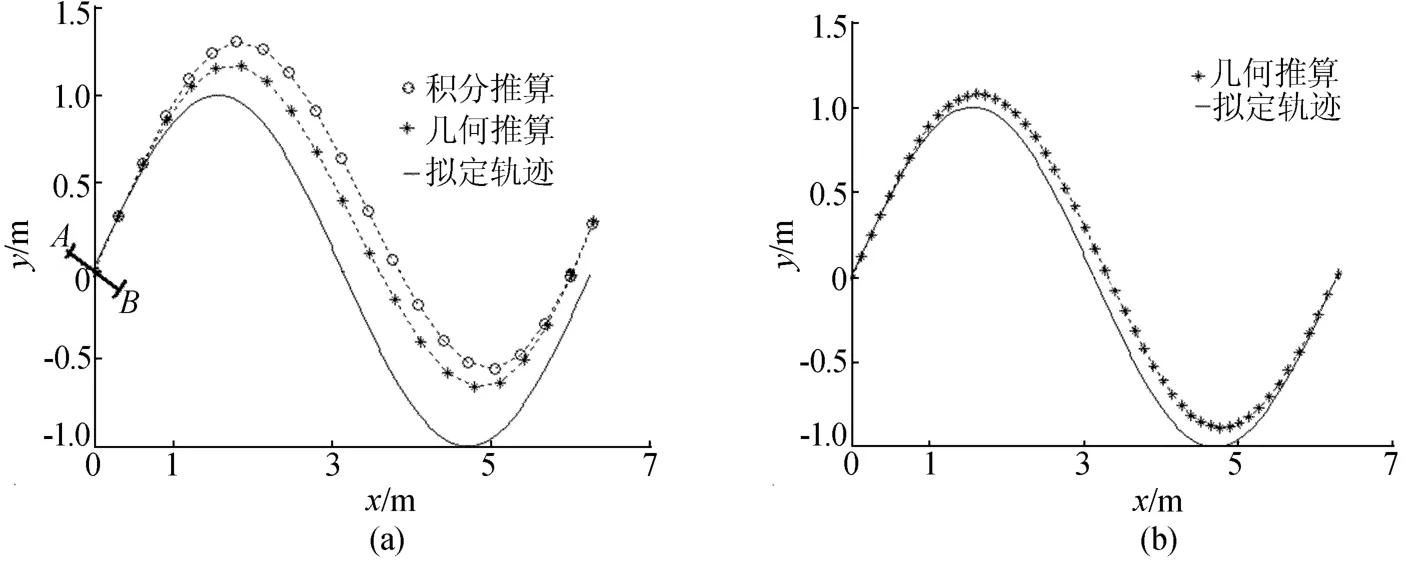
图5 采样误差为5%沿着正弦曲线行走仿真

3.5 仿真分析

圆弧、椭圆弧和正弦曲线段能组合机器人实际运动的所有可能的曲线,几何推算法能对这3种情况推算定位,所以几何推算法能对机器人的任何运动情况进行跟踪和定位。

本文几何推算法利用圆弧代替机器人的运动曲线,比积分推算定位用直线代替曲线的精度高。当然对于随机误差比较大的情况,几何推算法并不一定比积分推算的结果更好。由图4a可知,2种方法的结果差强人意,对于更大的随机误差,哪一种定位效果更好取决于随机误差的分布。从仿真实验可知,本文阐述的推算定位方法,速度采样最大误差不能偏离真值的5%,如果超过5%定位的精度情况不确定。在采样精度不变且误差小于5%的情况下,提高采样频率能有效地提高定位精度。

4 结束语

本文从运动和几何的角度,推导出一种新的基于双轮差动驱动的航迹推算方法。在采样精度和采样步数固定的情况下,该方法的推算定位精度比积分推算定位方法有较大地提高。在测量精度有限的情况下,通过提高采样频率可以有效地提高定位精度。和其它航迹推算定位一样,本文方法的误差积累无法通过其自身算法的改进来消除。同时对于其它意外的情况,如轮子打滑、转弯离心力所产生的偏移误差,也无法克服。当误差累积到一定量的时候,必须通过其它方法将累积误差消除,否则以后的推算定位将无效或失去意义。

一般情况下,本文论述的方法具有局部短期内高精度定位能力。将此法结合其它定位,如室内标签定位、超声波定位、UWB定位等,将会达到很好的定位效果。

[1]徐则中,庄燕滨.移动机器人定位方法对比研究[J].系统仿真学报,2009,21(7)：1891-1893.

[2]陈永光,李修和.基于信号强度的室内定位技术[J].电子学报,2004,32(9)：1456-1457.

[3]郑利龙,曹志刚.GPS组合导航系统的数据融合[J].电子学报,2002,30(9)：1384-1385.

[4]徐 德,邹 伟.室内移动式服务机器人的感知、定位与控制[M].北京：科学出版社,2008：237-238.

[5]柳长安,李国栋,刘春阳.差动驱动式移动机器人的运动规划[J].哈尔滨工业大学学报,2003,35(9)：1095-1096.

[6]吴克河,李 为,柳长安,等.双轮驱动式移动机器人动力学控制[J].宇航学报,2006,27(2)：272-274.

[7]Han S M,Lee K W.M obile robot navigation using circular path planning algorithm[C]//International Conference on Control,Automation and Sy stems,Seoul,Korea,2008：2082-2084.

[8]Chitsaz H,La Valle S M.Minmum wheel-rotation path for differential-drive mobile robots[C]//International Conference on Robotics and Automation,Roma,Itly,2007：2718-2719.

[9]Bobyr S,Lumelsky V.Control of dynamics and sensor based motion planning for a differential drive robot[C]//Proceedings of the IEEE International Conference on Robotics&Automation,Detroit,Michigan.1999：159-161.