基于横向模态差的桥梁横联构件损伤识别

赵 虎,蒲黔辉,施 洲

(西南交通大学土木工程学院,四川成都 610031)

基于横向模态差的桥梁横联构件损伤识别

赵 虎,蒲黔辉,施 洲

(西南交通大学土木工程学院,四川成都 610031)

讨论桥梁结构横向刚度的研究现状和影响因素,比较国内外规范关于横向刚度、横向水平变形限定的异同。文章提出用桥梁结构双侧响应模态差对结构的横向联系完整性进行评估,进而对桥梁结构的横向刚度进行探讨;通过比较全桥的双侧模态的响应差值曲线差异,对结构可能存在的损伤进行定位识别和初步的损伤程度识别。通过对一两跨连续钢桁架桥的有限元模拟分析,验证该指标对于横向联系完整性的评估和结构损伤识别的有效性和敏感性。

桥梁;横向刚度;双侧响应;模态差值;损伤识别

对于桥梁结构而言,不仅要具有足够的强度,还应具备足够的横向和竖向刚度以保证交通通行的安全舒适,避免结构与交通主体产生激烈的竖向和横向振动,同时维持结构自身的功能性。在既定材料研究水平前提下,若材料类型给定,就能比较容易地根据材料的特性对结构的强度进行合理的设计和评价。而对于结构的刚度,由于其不单纯只受材料的控制,更主要是受结构形式与体系布置的影响;所以对于刚度,尤其是横向刚度的设计和评价就显得较为困难。随着高速铁路的建设与发展,人们对结构竖向振动进行了较为详细的研究[1～3],而对于横向刚度的损伤识别研究相对薄弱。这不是偶然现象：对于一般跨度与常规结构体系的桥梁,由车辆通行安全净空界限所确定的桥梁横向刚度往往已经能够满足交通安全性与平稳性的要求,而且具有相当的安全储备,而对于大跨桥梁,非常规结构体系,则需要对其横向特性进行详细的探讨;此外,桥梁横向刚度的影响因素颇多,如线路不平顺[4～5]、宽跨比[6]、车辆蛇行[7～8]、墩梁相互作用[9～11],以及结构体系的布置[12]等。正是由于桥梁结构横向特性研究的复杂性,各国规范充分考虑到工程应用的方便性,对结构横向特性进行了指标化的限定,而由于切入点的不同,限定的方面也不尽相同。

1 国内外关于横向刚度限定的异同

桥梁作为一个复杂的动力学系统,对其刚度很难进行准确的定义,其物理意义也不甚明确。鉴于此,各国规范对桥梁刚度考虑的侧重点存在一定差异,规范指标值取得也不尽相同。

前苏联桥规(CH—200—62)对桥梁的横向刚度指标化为：T≤0.01l,T＜1.55s,其中：T为桥梁横向振动的基本周期,S;l为桥跨跨度,m。我国工程实践证明：某些桥梁没能满足此规定但运用良好,而有的桥很好地满足了此规定但实际运营情况欠佳。这说明此规范难以准确鉴别桥梁的真实运营状态,不能满足我国的工程实际需求。

德国关于桥梁横向刚度最初只是简单地通过限制其墩台横向水平位移来实现的。DS804规范规定在 V＞160 km/h区段由墩台横向水平位移引起的相邻结构轴线间的水平折角不得超过 1‰。这种在评价桥梁的横向刚度时只考虑桥梁下部支承结构而完全不考虑上部结构的影响的思路存在先天缺陷,所以,德国在随后新颁的 2003年新版铁路桥梁设计规范《Richtlinie804》增加了关于梁体横向自振频率的规定。

欧盟规范对桥梁上部结构水平变形的限值包括上部结构和下部结构(包括桩,支承条件和基础)。该规范通过限制上部结构的水平变形所引起的最大转角变化和变形曲线半径来对结构的横向刚度进行总体评价。

日本在 1992年的规范在明文条款中未对横向刚度做规定,但是在注释中认为横向水平挠度限值可以取为竖向挠度的一半,约为 L/3 600～L/5 000。列车活载作用下轨道面的变形量(折角变位和错位)应小于规范的限值。

我国《时速 200 km新建铁路线桥隧站的设计暂行规定》以及《京沪高速铁路设计暂行规定》都采用 L/4 000作为梁体横向变形的限值。鉴于墩台的横向变形计算和分析的复杂性,对于墩台的横向变形限值为Δ≤5 L。这一限值实际上是一个半经验半理论值,主要参考了前苏联桥规(CH—200—62)中的相关规定,并结合我国铁道勘察设计院以及国外近年的相关研究成果得来的。对于我国的铁路桥梁现状而言,当列车速度增加到一定程度后,大部分具有柔性墩的桥梁和部分建成较早的桥梁普遍存在横向振动过大的问题,数值大大超过《铁路桥梁检定规范》的参考阈值。对于墩的横向刚度问题,一般认为应该从动力学的角度考虑,墩的横向振动当与车辆 -轨道由于线路的不平顺造成的强制振动频率接近时,往往容易产生剧烈的共振问题。所以,对墩的横向刚度限值主要应该从尽量远离车辆 -轨道的共振频率的角度来讨论。

由上面的比较分析可以看出,桥梁的横向刚度、变形以及横向振动是一个涉及面非常广,分析难度大的系统性问题。在静力学中涉及了桩土效应、基础、结构体以及约束问题,在动力学方面涉及了车桥耦合振动的问题。因此,对这一领域还需要更深入广泛的研究,特别是关于横向刚度损伤识别问题的研究还相对匮乏,还有待进行相关的理论研究与探讨。

2 基于横向模态差的桥梁横联构件损伤识别理论

提出用桥梁双侧在激励作用下模态响应的差异来对结构的横向联系完整性进行评估,进而对桥梁结构的横向刚度进行探讨,并通过比较全桥的双侧模态的响应差异,对结构可能存在的损伤进行定位识别和初步的损伤程度识别。

在数量庞大的铁路公路桥梁结构中,有相当一部分都是横向对称设计的。对于横向对称布置的结构体系而言,尽管存在材质的不均匀性,构件施工精度的初始偏心缺陷等,亦或是在多线设计的桥梁结构中,列车荷载存在偏载,列车蛇行运动产生的横向随机振动,风荷载等非对称因素的影响,但从总体层面来看,仍然可以看作是对称的结构体系。从结构的对称性出发,由结构力学的知识可以知道,对称结构在对称荷载的作用下结构内力也是对称分布的。将这一思想类比应用到桥梁结构中来,当结构受到外界激励作用时,桥梁两侧的对应控制点的响应应保有一定的一致性。这个一致性指激励作用下两侧的响应差异不应太大,具体地讲,即同一纵向位置上桥梁两侧对应的模态差值应保持在较小的水平。

从广义的角度看,结构的横向刚度由横向弯曲刚度和扭转刚度两部分组成。以扭转刚度为例加以说明,若结构的扭转刚度大,激励强度水平一定,则结构两侧对应控制节点间产生较小的响应差异 Δ,若结构的抗扭刚度不足,扭转变形大,则结构两侧对应控制节点间将产生较大的响应差异Δ′。结构扭转示意见图1。

图1 结构扭转示意

同理,在同样的激励条件下,若结构横向联结充分,则结构两侧对应的控制节点响应的同步性更好,如图1中所示的 Δ与 Δ′就更接近;若结构的横向联系不足,或是横联存在损伤,则双侧对应控制节点间的一致性就差,图中所示的 Δ与 Δ′差异就较大。如图2所示。

图2 结构横向联系强弱示意

对于新建桥梁,在建成运营初期,结构尚处于未损伤的状态时,可及时对桥梁双侧对应控制点的模态进行实测存档,作为日后损伤和性能评估的参考依据。对于已建桥梁,若已无法取得原始的模态信息,则可利用此方法对桥梁进行定期的实测,以此作为损伤和性能评估的指标。

测得结构双侧响应后,由其双侧对应点的响应差值 S=X(t)R-X(t)L可绘出外部激励下结构的差值曲线。若结构未损伤,则差值曲线 S(x)在全桥范围内除在端部支座处和中部支座处幅值变化较大外,其余位置应保持相对平顺的线形。若结构某位置的横向联系存在损伤,则差值曲线 S(x)在损伤位置附近会表现出如尖峰,反弯,数值突变等异常。

3 横联构件损伤识别的数值模拟及分析

3.1 有限元模型建立及损伤工况的定义

为验证指标 S(x)对于横联损伤的有效性和灵敏性,以一两跨连续钢桁架桥进行数值模拟分析。桁架为等节间布置,每个节间跨度 6m,共 26节间。总跨156m。第 1、13节间设有固定铰支约束,第 26节间设活动铰支约束。两线加载。损伤设置分不同程度的单位置损伤和多位置损伤。在第 5、15节间设置程度分别为 5%、10%、15%和 30%的单位置横联构件损伤;在第 9、18节间设置程度分别为 5%、10%、15%和30%的双位置构件损伤。构件损伤采用刚度降低进行模拟。建立基于 MidasCivil的结构有限元计算分析模型,如图3所示。节间布置如图4所示。

图3 钢桁架计算分析有限元模型

图4 钢桁架节间布置

3.2 结构自振特性分析

结构有限元计算模型建立后,可计算其自振频率在损伤水平 15%下的值,如表1所列。

表1 结构自振频率特性

此处只列出未损伤状态和横联损伤 15%水平下的自振特性。有限元计算结果表明：本结构主要受横向性质控制,其前两阶模态都由侧倾控制,且在不同损伤级别下各阶模态的出现顺序并没有发生改变。从自振频率的改变率可以看出,在 15%的损伤水平下结构前 6阶模态中降低最大为0.056 0%,前 10阶最大降低为0.063 3%。计算表明：即使在 50%的横联损伤水平下,结构的频率降低也是十分有限的。在前 6阶模态中降低最大0.269 5%,前 10阶模态内降低最大仅为0.288 5%,由此看出,结构自振频率作为结构整体性能的衡量指标,对结构的局部损伤表现稍显迟钝。在 3阶、4阶模态某些损伤位置,自振频率不降反增。若借助频率改变来识别结构的局部损伤,在频率测试精度上还需提高,对结构的损伤位置的识别也还需要更进一步的研究。

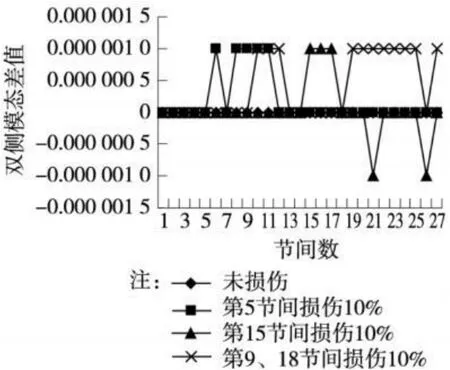
图5 DX差值曲线

图6 DY差值曲线

3.3 利用双侧响应模态差值曲线 S(x)对结构进行损伤识别

(1)损伤位置的识别

当设置的横联构件刚度损伤 10%时,可得双侧响应模态差值曲线 S(x),如图5～图10所示。

图7 DZ差值曲线

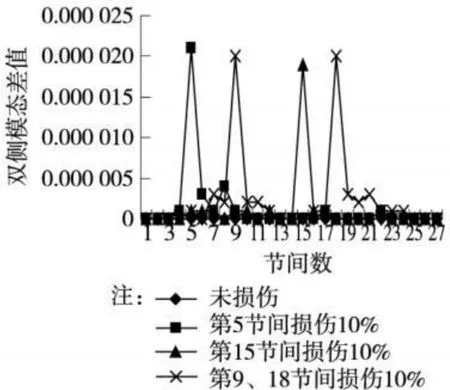
图8 RX差值曲线

图9 RY差值曲线

图10 RZ差值曲线

从图中可以看出,结构在横联刚度损伤 10%时的双侧响应模态差值曲线 S(x)在设置的损伤位置表现出异乎寻常的变异,与设置损伤位置显示一致。通过图5～图10图形间对比发现,对于本模型而言,除在DX自由度上的差值曲线在包含真实损伤变异的前提下产生少数意义不明确的突变,如尖峰,数值突变等,其他自由度上均能准确反映损伤的位置。造成 DX自由度上识别困难的原因在于本结构在 X方向上的响应主要是由竖向和纵向性质以及所施加的约束种类和约束水平控制的,受横向控制相对较弱。试验模拟表明,双侧模态差值曲线能够很好地识别 10%刚度损伤水平下的损伤位置。

同样的结论在损伤水平 5%,15%和 30%的双侧响应模态差值曲线 S(x)中也能得到很好的印证,在此对损伤水平 5%,15%和 30%的双侧响应模态差值曲线S(x)不作一一列举。从各自由度的 S(x)曲线对比可以看出,对于本模型,平动自由度的损伤敏感性和精确性整体弱于转动自由度。因此,精确考量实际结构的转动自由度显得十分重要。而平动自由度当中 DZ优于DY,DX显得最差。这主要是由于 DX主要由结构的竖向和纵向的性质等而非横向刚度性质控制。综上,S(x)曲线对于识别结构的损伤位置能取得理想的效果。

(2)损伤程度的识别

实际上,S(x)曲线对于结构损伤程度的识别也是可行的。通过结构有限元计算分析,得出结构在不同损伤级别下各个位置的 S(x)曲线,如图11～图14所示。

图11 第5节间模态差值曲线

图13 第 9,18节间 RY模态差值曲线

图14 第 9,18节间 RX模态差值曲线

对比图11～图13可以发现,结构在不同损伤程度下其 S(x)曲线峰值幅值显著变化,损伤位置指示准确。观察图13发现,结构在多点损伤状态下,不同点位在同一损伤级别下 S(x)曲线峰值往往不同。从图13中可以看到第 18节间的损伤易于发现,而第 9节间的损伤则容易被忽略,而在图14中则可以明显观察到双点损伤。所以,在实际应用中,应该认真比对不同自由度下的 S(x)曲线特性,防止漏判结构的潜在损伤。

(3)跨内与支座损伤对比识别

由于结构的跨中位置动力响应往往较其他位置明显,而越接近支座位置,受到支座的约束作用越明显,动力响应也就随之降低,给结构支座处的损伤识别带来额外的难度。而支座的性能对于结构的影响是深刻的,关系结构整体的性能;因此,对支座的损伤识别十分必要。现对结构在接近跨中和支座处损伤识别情况比较如下。

图15中显示：结构在第 5节间接近跨中位置和第15节间靠近支座位置处损伤识别结果明显,尖峰突出,位置明确。在第 14节间支座处,同样的损伤水平下峰值明显降低,响应差值突降,降低了约 75%,这主要是因为结构在支座位置处受到了支座强有力的约束作用,致使响应低下,损伤变异也不明显,这在实际应用中势必会给识别带来额外的困难;所以对支座的损伤识别应做到全面,细致,防止漏察错判。

图15 不同位置 RY模态差值曲线

4 结语

本文简要介绍了桥梁结构横向刚度的研究现状和主要影响因素,比较了国内外规范关于横向刚度、横向水平变形限定的异同。简述了我国在铁路桥梁结构横向刚度领域的理论研究现状和工程实践的应用现状。提出用桥梁结构双侧响应模态差值 S=X(t)R-X(t)L对结构的横向联系损伤状况进行评估;通过比较全桥的双侧模态的响应差值曲线 S(x)差异,对结构在横联损伤进行定位识别和初步的损伤程度识别。通过有限元数值模拟分析,验证了结构在 5%、10%、15%等不同损伤水平下、不同损伤位置时,该方法应用于横向联系完整性评估以及结构损伤识别的可行性;同时讨论了支座处损伤及多点损伤识别的特殊性。

[1]Apiwan Wiriyachai.Impactand Fatigue in Open Railway Truss Bridge Thesis[D].IIT,dec.1980.

[2]晋智斌,强士中,李小珍.高速列车 -桥梁竖向随机振动的时域分析方法[J].地震工程与工程振动,2008(3)：110-115.

[3]苏木标,李建中,梁志广.铁路简支梁桥竖向有载频率研究[J].铁道学报,2001,23(2)：76-80.

[4]王福天.车辆动力学[M].北京：中国铁道出版社,1981.

[5]曹雪琴,陈松.轮轨蛇行引起桥梁横向振动随机分析[J].铁道学报,1986(1).

[6]郭向荣,刘庆艳,曾庆元.高速铁路大跨度钢桥横向刚度限值分析[J].中国铁道科学,2001(5)：29-33.

[7]王荣辉,郭向荣,曾庆元.高速列车 -钢桁梁桥系统横向振动随机分析[J].铁道学报,1996(1)：90-95.

[8]汪 胜,王庆波,夏 禾,等.高速铁路双线简支梁空间振动响应分析[J].北方交通大学学报,1998(4)：37-40.

[9]柯在田,张 煅.铁路桥梁横向变形限值标准问题的研究[J].铁道标准设计,2004(7)：129-134.

[10]李运生,阎贵平,王元清,等.铁路桥墩横向刚度设计标准的研究[J].铁道科学与工程学报,2007(1)：44-48.

[11]马坤全,曹雪琴.列车通过高墩连续梁桥横向振动分析[J].上海铁道学院学报,1994(1)：9-18.

[12]杨仕若.拱桁组合体系桥横向刚度分析[J].中南土木学院学报,2006(3)：94-97.

U 441+.4

A

1004-2954(2010)07-0077-04

2010-02-04

铁道部科技研究开发计划重大课题(2008G032-10)。

赵 虎(1986—),男,硕士研究生,E-mail：zhaohu19860412@126.com。