一种新的BOC调制无模糊跟踪鉴别器设计

唐 斌,郭盛桃,刘 富

(61081部队,北京 100094)

0 引 言

未来的GNSS系统要求实现频段共用同时实现频谱分离,BOC(Binary Offset Carrier)调制是为适应这一发展需要提出的一种新的调制方式。BOC调制及其变形信号的接收处理算法在GPS现代化的接收机、Galileo接收机、中国新一代卫星导航系统的接收机中都将是极其重要的研究内容[1]。BOC调制是通过将扩频码与一个频率为扩频码速率的整数倍的方波副载波相乘得到。BOC调制的相关函数具有更好的性能,其相关函数相对相同码速率的BPSK方式更陡峭,从而具有更高的码跟踪精度和更好的多径分辨能力。但由于BOC调制的自相关存在多个峰值,从而使得鉴别器曲线存在错误锁定点,增加这种信号的捕获难度和错误跟踪的可能性。用于BOC调制的无模糊捕获方法,如BPSK-like方法[2]、副载波相位消除技术(Sub Carrier Phase Cancellation)[3]等,同样可以用于无模糊跟踪。BPSK-like方法相关函数的计算会造成3 dB的信噪比损失;副载波相位消除技术则需要两个通道平方相加,从而造成平方损耗。从建立码跟踪延迟锁定环数学模型出发,详述了BOC调制信号的跟踪模糊问题,基于BOC调制机理,给出一种新的适用于无模糊跟踪的鉴相器算法。

1 码延迟锁定环的数学模型

1.1 码延迟锁定环结构

延迟锁定环的一般结构如图1所示。输入信号经前端滤波器滤波、载波剥离后与本地码超前路(Early)、即时路(Prompt)、和滞后路(Late)相乘并累加得到 IE、IP、IL、QE、QP 以及QL。

输入信号通过与本地载波混频,然后与本地码的超前、即时和滞后路进行积分累加,则第k次累加输出可表示为I路和Q路相关器第k个输出,可以用以下两个公式计算

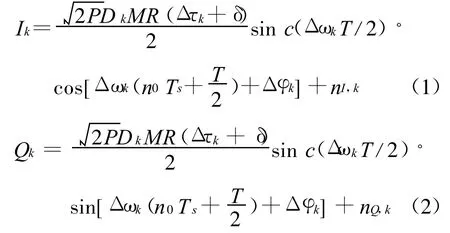
对于超前 IE、QE,即时 IP、QP 和滞后 IL、QL分支分别有δ=d·Tc,δ=0,δ=-d·Tc,d表示相关器间距,即超前码或滞后码与即时码的延迟;Tc表示一个码片的时间宽度。这些积分累加值送入DLL鉴别器产生码延迟误差估计,延迟误差估计值通过环路滤波器滤波用来更新本地码NCO,从而补偿跟踪过程的码延迟误差。

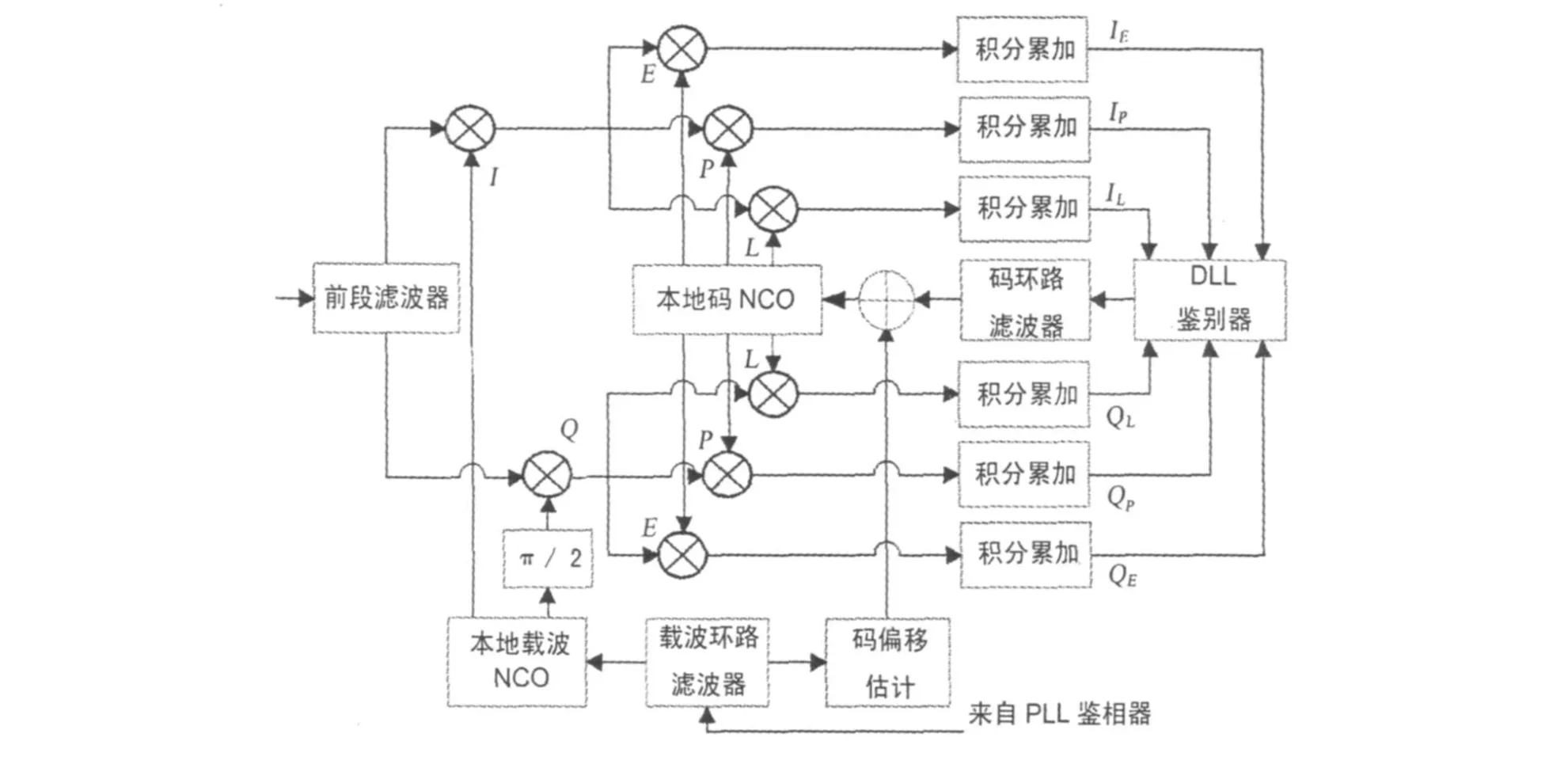
图1 延迟锁定环结构

1.2 DLL鉴别器数学分析

在导航接收机中,广泛使用的码跟踪环鉴别器主要为:非相干型点积(Dot Product,用DP表示)鉴别器和非相干型超前减滞后功率(Early Minus Late Power,用EMLP表示)鉴别器。这两类鉴别器数学表示为

假设载波完全跟踪上,且不考虑噪声的影响,由式(1)、(2)(幅值归一化)得

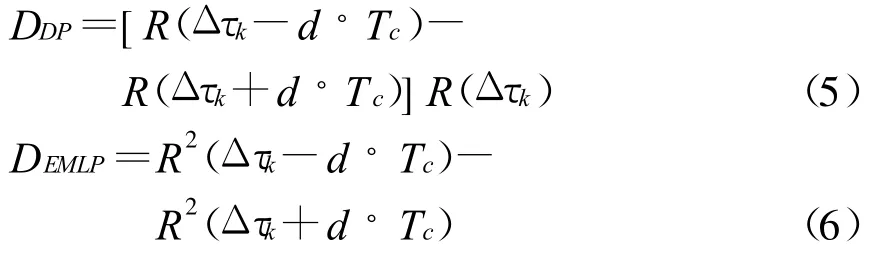
对于Galileo L1F BOC(1,1)信号,则R(·)为[4]

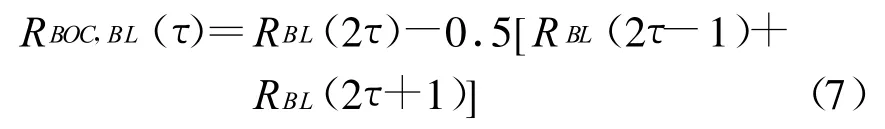
式中:RBL为GPS C/A码的自相关函数。

码跟踪环对于输入码相位误差Δτk的跟踪范围为|Δτk|≤d·Tc。图2为相关器间距 d为0.2码片时,BOC(1,1)调制的 L1F码鉴别器输出曲线,图2(a)为DP鉴别器在不同前端滤波器带宽下的输出,图2(b)为EM LP鉴别器在不同前端滤波器带宽下的输出。由Galileo L1F码的频谱特性可知,L1F码的主瓣宽度为4.092 MHz,在图2中取前端滤波器带宽分别为4 MHz和2 MHz进行对比。

从图2中可以看出:

前端滤波器带宽越宽,线性跟踪区域越长,C/A码的线性跟踪区域斜率明显比BOC(1,1)小。

由于平方的作用,使得EMLP鉴别器受前端滤波器的影响更大;由于乘以即时路相关累加值,使得DP鉴别器线性跟踪直线区域很窄。

对于BOC调制的信号,可能会发生错误锁定,如果环路锁定在错误锁定点,无疑会大大加剧测距误差。例如滤波器带宽为无限带宽和4 MHz时的±0.6点,滤波器带宽为2 MHz时的±0.7点。

图2中,由于BOC调制的自相关存在多个峰值,从而使得鉴别器曲线存在错误锁定点,对于BOC(n,m)调制,也会出现类似的错误锁定情况。下面从BOC调制的机理出发,阐述一种新的BOC调制无模糊鉴别器设计。

2 BOC调制机理分析

BOC调制包括两部分:一是PRN码调制;二是副载波调制。可以分别表示为

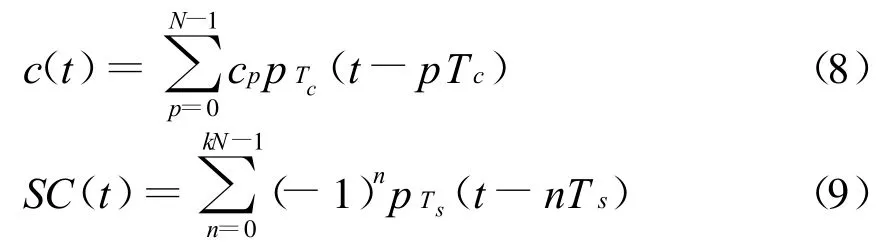
式中:cp为PRN码序列值;Tc为一个码片长度;pTc为长度Tc的矩形脉冲;Ts为副载波周期的一半;pTs为长度Ts的矩形脉冲;N为一个码周期码片数;码周期 T=NTc=kNTs。对于BOC(1,1),Tc=1/1.023e6,Ts=1/(2*1.023e6),k=2,如图3所示。对于BOC(n,m),Tc=1/(m×1.023e6),Ts=1/(2×n×1.023e6),k=2n/m,BOC调制的导航信号n一般为m的整数倍,则k为偶数[5]。

图3 BOC调制结构解析

整个BOC调制可以表示为

式中:[n/k]表示向下取整,表示在每个码片末依据码序列值判断是否需要变号。

3 BOC调制的无模糊跟踪

设接收机本地产生的BOC调制码序列为

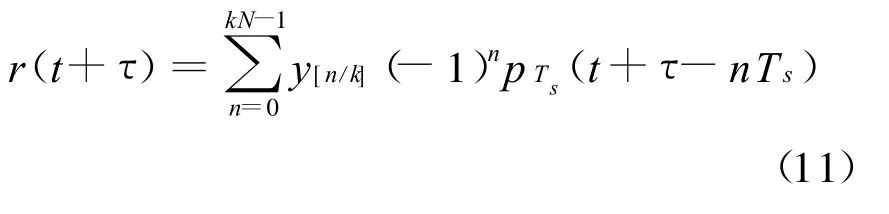
则相关函数为(设延迟τ=lTs)

不妨假设本地产生的码仅为PRN码[6]

设τ=l Ts,则产生一种新的相关函数为

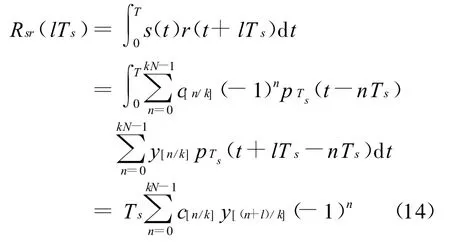
将Rsr(lTs)简化表示为Rsr(l),下面分析Rs r(l)的性质,首先分析Rsr(l)的奇偶性

式中:n-l=m,当 l为奇数时,Rs r(l)则为奇函数。

其次分析l为偶数时,Rsr(l)的函数特性。由上面分析,k为偶数,设k=2h。将式(14)中n分别按奇数和偶数表示,则

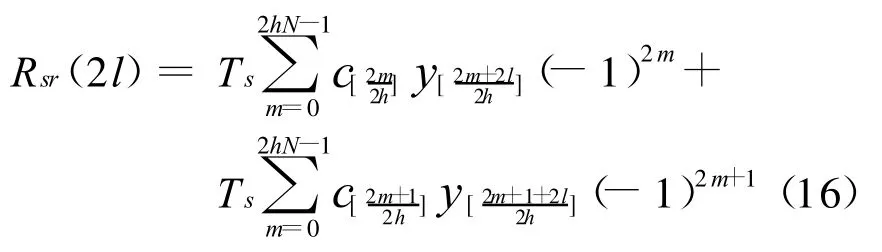
由于k=2h是不小于2的整数(BOC(1,1)时取2),则1/(2h)≤0.5,对于向下取整时

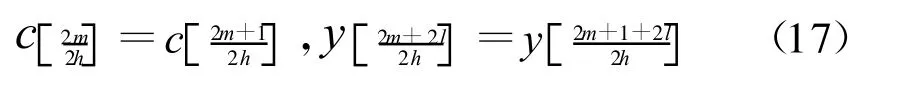
则式(16)变为

由式(15)和(18)得:新的相关函数在码延迟奇数倍Ts时为奇函数,在码延迟偶数倍 Ts时为0,正好符合码鉴别器特性。

4 仿真验证

以BOC(1,1)和BOC(2,1)为例对新的鉴别器设计进行验证。对于BOC(1,1)调制,k=2,则l=1时,τ=Ts=Tc/2,此时BOC与PRN相关值为0.5;l=-1时,τ=-Ts=-Tc/2,此时 BOC 与PRN相关值为-0.5;l=±2时,τ=±Tc,此时相关值为0。鉴别曲线如图4所示。

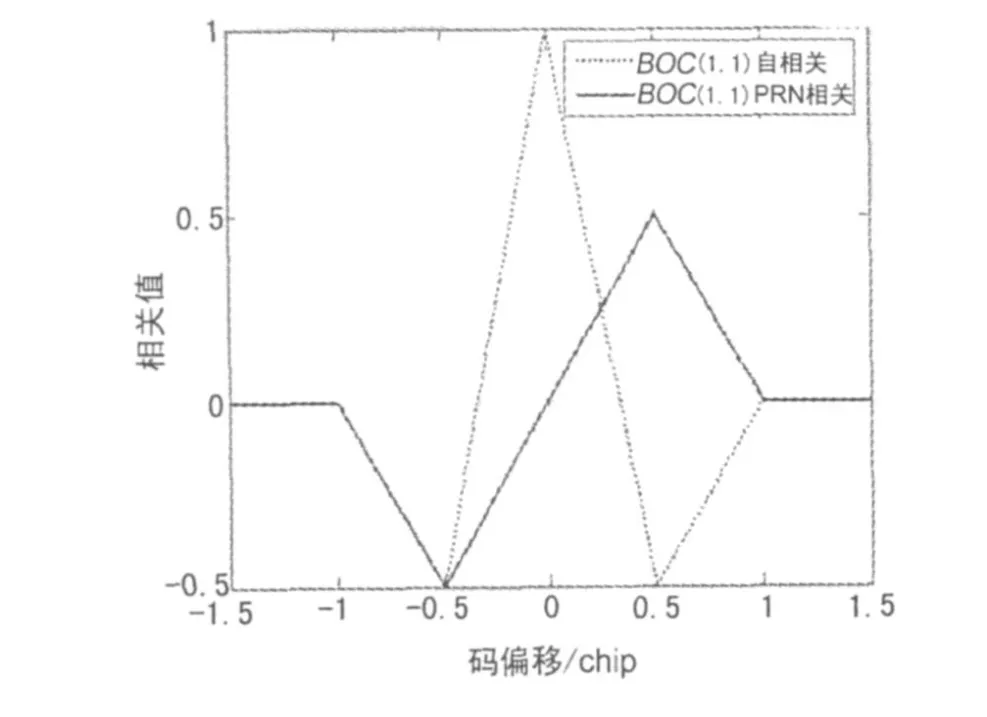
图4 BOC(1,1)自相关及与PRN相关

对于BOC(2,1),k=4,则l=±1和 l=±3时,τ分别为 ±Tc/4和3Tc/4,此时 BOC与PRN相关值分别为±0.25和±0.25;l=±2和l=±4时,τ分别为±2Tc/4和±Tc,此时相关值为 0。鉴别曲线如图5所示。

图4、图5中的 BOC(1,1)和 BOC(2,1)与其相应伪码的相关函数均有较好的鉴别特性,将其应用于码跟踪,无疑可以完全消除DP鉴别器和EMLP鉴别器的模糊跟踪,并可以方便地推广到BOC(n,m)中去。当然该鉴别方法也有一定缺陷,即线性跟踪区域的斜率最高只为1,明显小于EMLP和DP鉴别器。在导航接收机中具体应用时,设BOC与其PRN的相关函数为RBP(·),BOC的自相关函数为RBOC(·),再构造一种新的相关函数:

图5 B OC(2,1)自相关及与PRN相关

将RN(·)分别应用于DP和EMLP鉴别器,如图6所示。图中BOC(1,1)调制,相关器间距为0.1码片,前端滤波器带宽为无限带宽,EMLP鉴别器线性跟踪区域的斜率达到了9,即使是DP鉴别器线性跟踪区域的斜率也明显高于1。在消除模糊跟踪上,仅有一定程度的轻微振荡,可以说是性能优良的无模糊鉴别器。

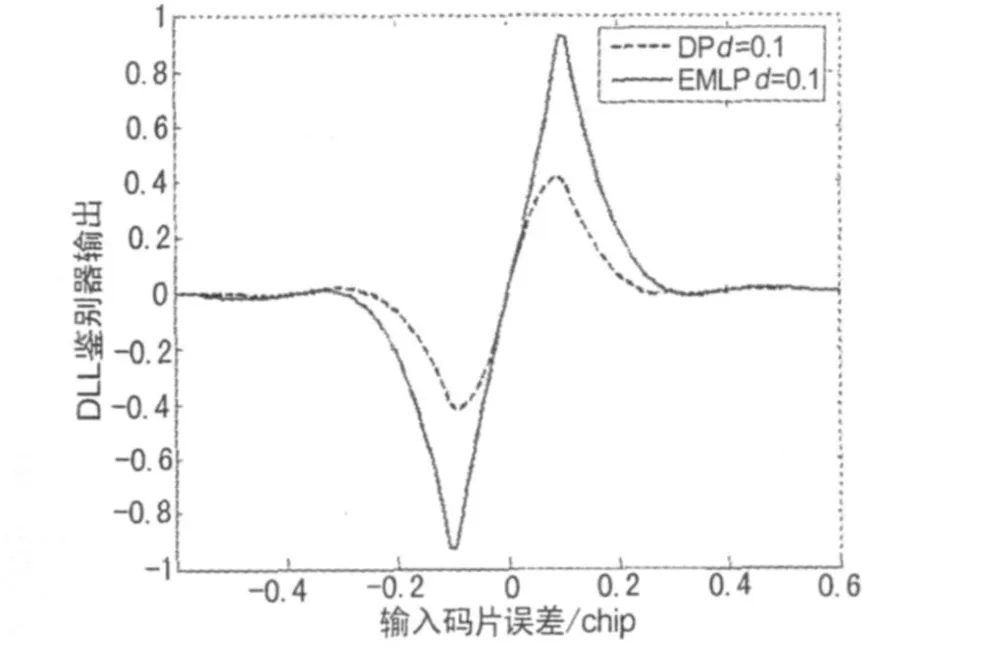
图6 新的相关函数在DP和EMLP鉴别器中的应用

5 结 论

BOC调制方式是未来卫星导航系统信号设计的发展方向,BOC调制信号的相关函数的多峰结构造成的模糊,在接收时需要采取一些特殊处理来消除。通过改变本地码的生成方式,构造了一种新的相关函数结构,进行数学描述,论述了作为BOC调制码鉴别器,进行无模糊跟踪的可行性。对于其在BOC调制及其变形信号导航接收机码捕获、跟踪等方面的具体应用仍有待进一步研究。

[1]杨东凯,刘宪阳.低信噪比条件下BOC信号的快捕算法研究[J].中北大学学报,2008,29(3):281-284.

[2]Martin N,Leblond V,Guillotel G,et a1.BOC(x,y)signal acquisition techniques and performances[C]∥ION GPS/GNSS 2003,Portland,2003:188-198.

[3]Vincent H,Daniel R,Lionel R,et al.Analysis of Non Ambiguous BOC Signal Acquisition Performance[C]∥ION GNSS 2004,Long Beach,2004:2611-2622.

[4]Olivier J.Design of Galileo L1F Receiver T racking Loops[D].Ph.D.dissertation,University of Calgary,2005.

[5]Olivier J,Christophe M,Elizabeth C M,et al.A New Unambiguous BOC(n,n)Signal Tracking Technique[C]//Proceedings of the European Navigation Conference GNSS,Rotterdam,The Netherlands,2004:43-44.

[6]Maristella M,Andrea F,Carlo S R.A New Fine T racking Algorithm for Binary Offset Carrier Modulated Signals[C]// ION GNSS 2006,Fort Worth,2006:834-840.