具有转向点的奇摄动二阶拟线性边值问题

许国安，余赞平

（1.华侨大学数学科学学院，福建泉州362021；2.福建师范大学数学与计算机科学学院，福建 福州 350007）

具有转向点的奇摄动二阶拟线性边值问题

许国安1，余赞平2

（1.华侨大学数学科学学院，福建泉州362021；2.福建师范大学数学与计算机科学学院，福建 福州 350007）

研究具有转向点的奇摄动二阶拟线性边值问题.在缺乏弱稳定的条件下，考虑具有转向点的二阶拟线性边值问题，利用经典的上、下解方法，证明边值问题解的存在性，并给出了解的一致有效估计.

转向点；边值问题；奇摄动；二阶拟线性

转向点问题是奇摄动理论的重要内容，在量子力学、流体力学、光的传播，以及化学反应等物理、化学现象中广泛出现［1-2］.许多学者对此问题做了大量研究［3-7］，而这些工作都是在假设弱稳定条件下完成的.本文在缺乏弱稳定的条件下，考虑了具有转向点的二阶拟线性边值问题.

1 基本假设

主要考虑的边值问题为

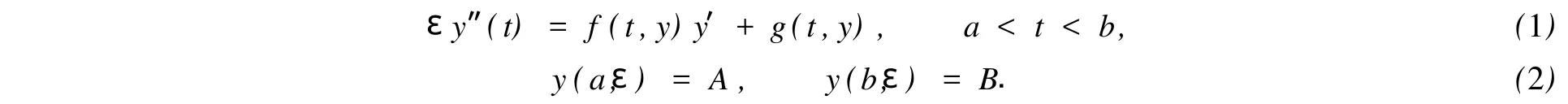
对于边值问题（1），（2），作如下3点假设.

（H1）退化问题

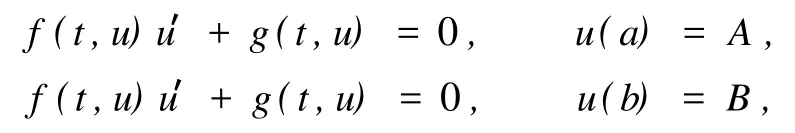
分别存在解u1=u1（t）∈C2［a，t0］与u2=u2（t）∈C2［t0，b］，t0∈（a，b）.

假设，有

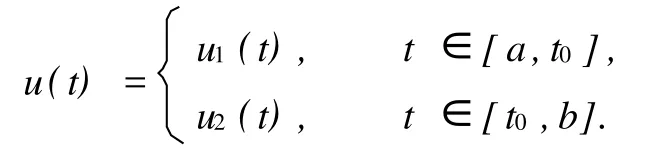
然后，再预设区域有

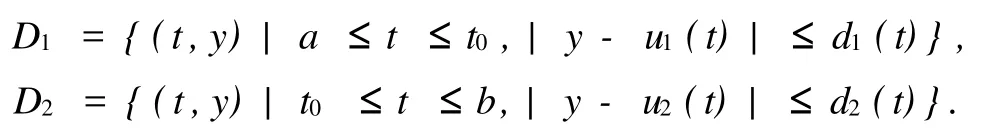
其中：d1（t），d2（t）为正的连续函数；δ≤d1（t），d2（t）≤|u2（t0）-u1（t0）|+δ，并且有

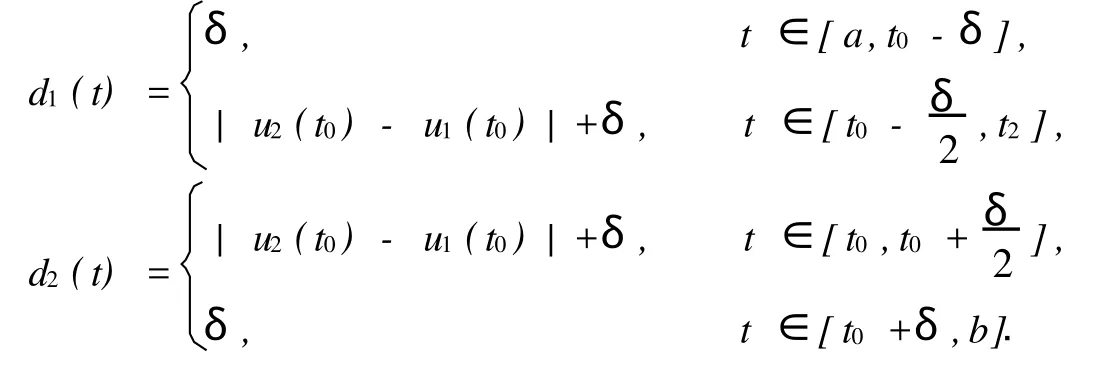
其中：δ为适当小的正数.

（H2）设f（t，y），g（t，y）在D1∪D2上充分光滑.

（H3）设t=t0为边值问题（1），（2）的m阶转向点，有

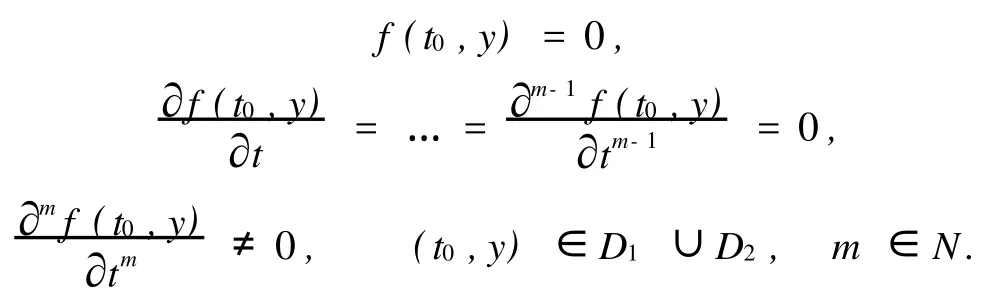
可以对转向点的阶数作拓广，即

在拓广意义下，研究转向点问题.为了描述的方便，作如下定义.

定义1 函数u（t）在［a，b］中是（Ⅰq）稳定的，如果存在正常数k，使得h（t，u（t））≡0，a≤t≤b，0≤j≤2q，且在D1∪D2上h（t，y）≥k＞0.其中：当t∈［a，t0］，h（t，y）=f（t，y）u′1（t）+g（t，y），当t∈［t0，b］，h（t，y）=f（t，y）u′2（t）+g（t，y）.

定义2 函数u（t）在［a，b］中是（Ⅱn）稳定的，若u（a）≤A，u（b）≤B，且存在一个正数k，使得h（t，u（t））≥0.当a≤t≤b，1≤j≤n-1，且在中，h（t，y）≥k＞0.其中：=｛（t，y）|a≤t≤b，0≤y-u（t）≤δ｝.

定义3 函数u（t）在［a，b］中是（Ⅲn）稳定的，如果u（a）≥A，u（b）≥B，而且存在一个正数k，使得（je）h（t，u（t））≥0（≤0）.当a≤t≤b，1≤j0，je≤n-1，且在中，h（t，y）≤-k＜0（≥k＞0）.其中：j0（je）表示一个奇（偶）整数.若n是偶（奇）整数，=｛（t，y）|a≤t≤b，-δ≤y-u（t）≤0｝.

2 主要结果

引理1 如果假设H1，H2成立，而且退化轨道u（t）在［a，b］中是（Ⅰq）或（Ⅱn），（Ⅲn）稳定的，则有u1（t0）=u2（t0）.

证明 不妨设退化轨道是（Ⅱn）稳定的（另两种稳定情形的证明类似）.

令h（t，y）=f（t，y）u′（t）+g（t，y）.假设u1（t0）≠u2（t0），u1（t0）＜u2（t0），则有

这与f（t0，u1（t0））u′1（t0）+g（t0，u1（t0））-f（t0，u2（t0）u′2（t0））-g（t0，u2（t0））=0矛盾.

同理可证，当u1（t0）＞u2（t0）时，也存在矛盾，故假设不成立.即u1（t0）=u2（t0）.

由引理1的结论可知，在假设稳定的条件下，满足左右边界的退化解在转向点处一定是相连的，即退化轨道是连续的.

定理1若假设H1，H2，H3成立，且退化轨道u（t）是（Ⅰ0）稳定的.则存在ε0＞0，使得对于0＜ε≤ε0时，边值问题（1），（2）存在解y=y（t，ε），并满足

|y（t，ε）-u（t）|≤v1（t，ε）+εcp.

证明 不妨假定u′1（t0）≤u′2（t0），对于t∈［a，b］和ε＞0，定义

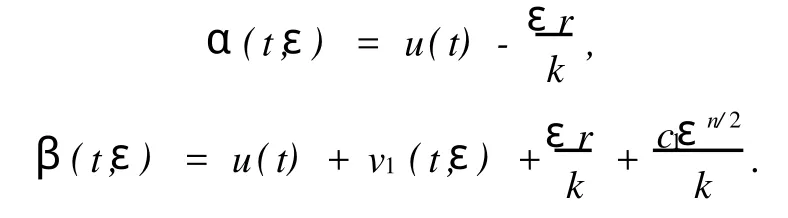
其中：c1为某一充分大的正数；r≥|u″0|.

上式中：ξ介于u（t）与α（t，ε）之间；t∈［a，t0）∪（t0，b］.

至于β，注意到v1是εv″=kv在（a，t0）∪（t0，b）中的解，满足

且

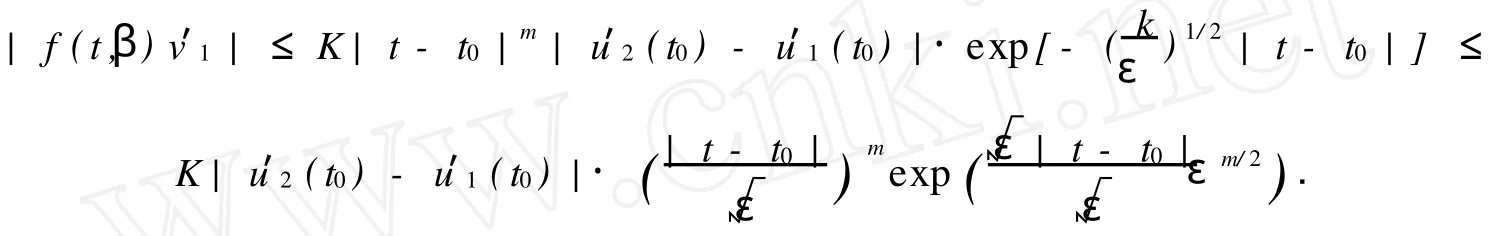
其中：K为某一适当大的正数.

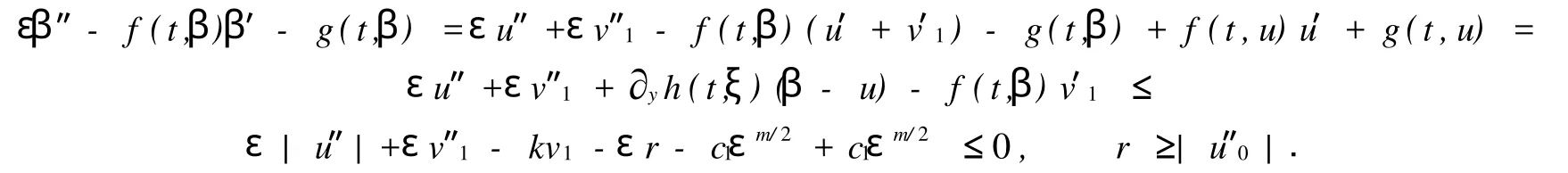
α，β分别是边值问题（1），（2）的下解与上解.故由二阶微分方程微分不等式理论［6］可知，边值问题（1），（2）存在解y=y（t，ε）满足

|y（t，ε）-u（t）|≤v1（t，ε）+εcp.

当0＜n＜2时，p=m/2；而当m≥2时，p=1.

定理2 假设H1，H2，H3成立，且退化轨道u（t）是（Ⅰq）（q≥1）稳定的.当转向点的阶数m＞1+1/q时，存在ε0＞0，使得对于0＜ε≤ε0时，边值问题（1），（2）存在解y=y（t，ε），满足

证明 类似于定理1的证明.假定u′1（t0）≤u′2（t0）.对于t∈［a，b］和ε＞0，定义

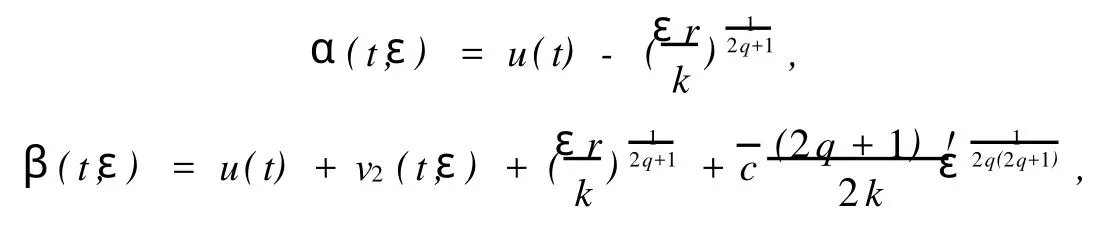
类似于定理1，α在t=t0点不一定可微，但有，且

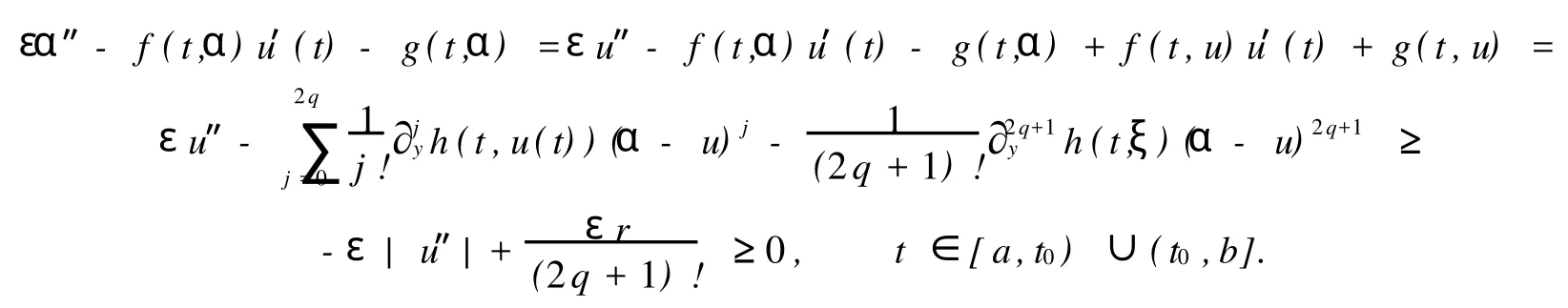
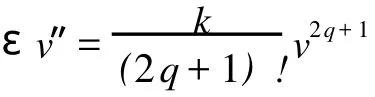
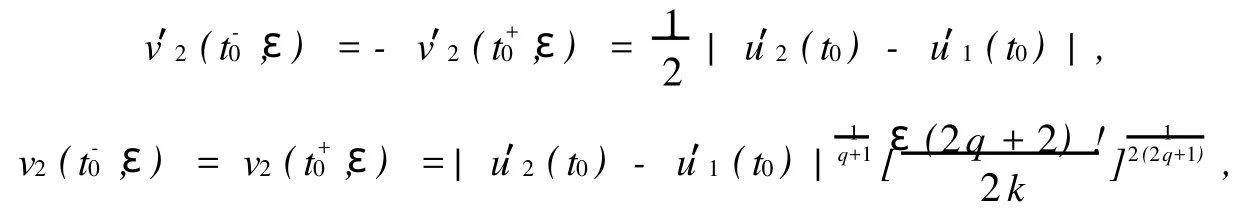
且

因此，β在t0点可微，且有

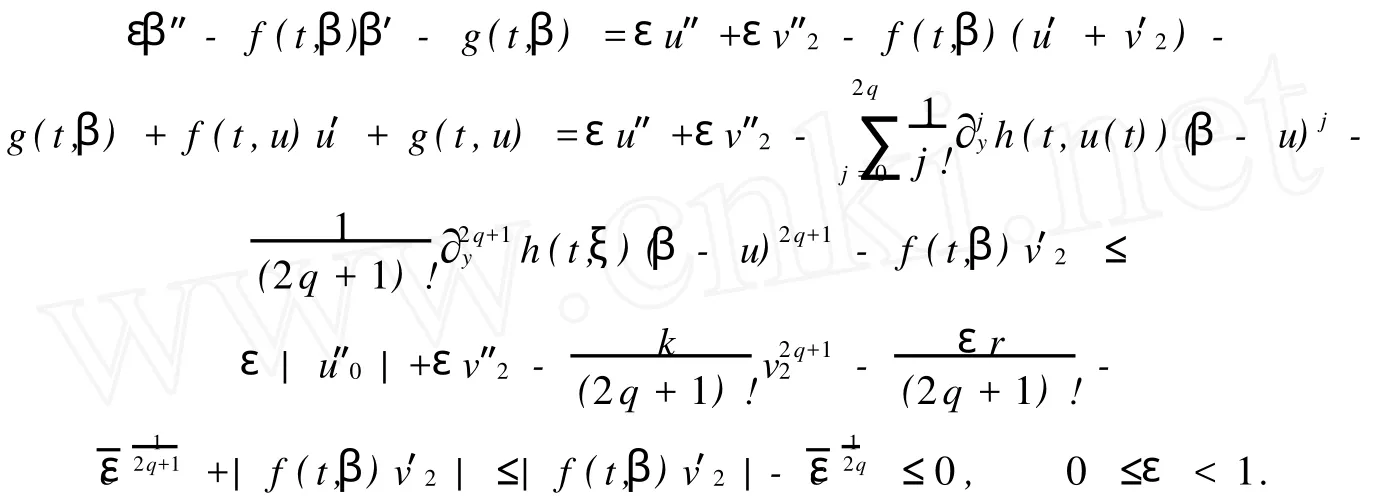
α，β分别是边值问题（1），（2）的下、上解.由二阶微分方程微分不等式理论［6］可知，边值问题（1），（2）存在解y=y（t，ε），满足

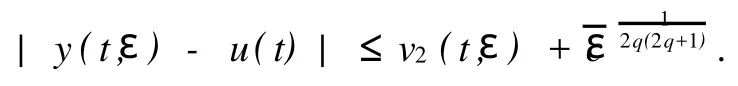
若退化轨道u（t）是Ⅱn或Ⅲn稳定时.

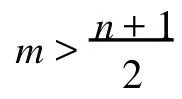
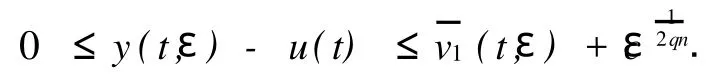
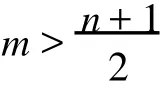
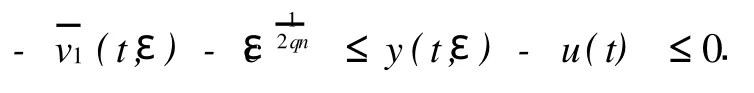
以上讨论，对Robin边值问题

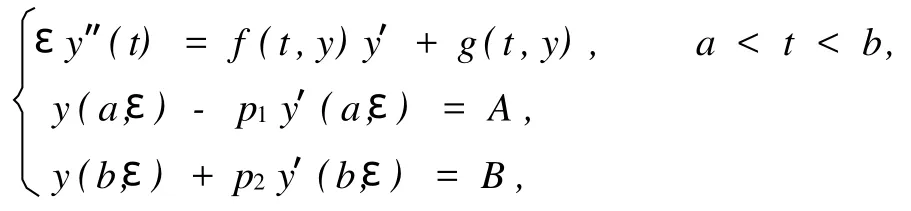
同样也是有效的，且可得到类似的结论.

3 例子

如边值问题

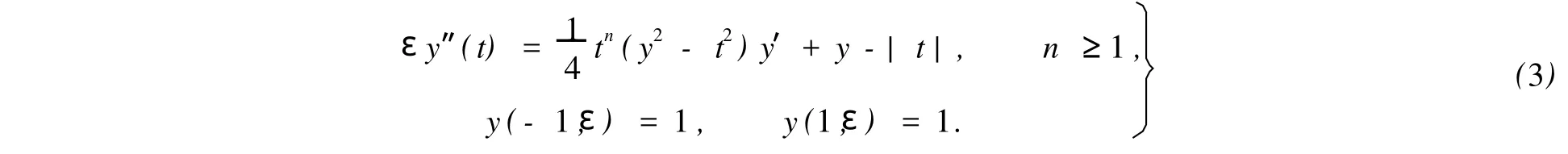
易求得退化问题

式（4），（5）分别存在解u1=-t与u2=t，且u1（0）=u2（0）=0，u′1（0-）=-1≠u′2（0+）=1.

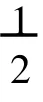
|y（t，ε）-|t||≤v1（t，ε）+εcp.

［1］NAYFEH A H.Perturbation methods［M］.New York：Wiley，1973.

［2］O’MALL EY R E Jr.Introduction to singular perturbations［M］.New York：Academic Press，1974.

［3］周软德.具有转向点的奇摄动边值问题［J］.东北数学，1986，2（1）：100-110.

［4］蔡建平，林宗池.具有转向点的三阶半线性奇摄动边值问题解的存在性［J］.应用数学和力学，1993，14（12）：1035-1039.

［5］吴钦宽，张祥.具有转向点的奇摄动非线性边值问题解的一致有效估计［J］.应用数学，1995，8（2）：231-238.

［6］章国华，侯斯FA.非线性奇异摄动现象：理论和应用［M］.福州：福建科学技术出版社，1989：6-15，28-31.

［7］吴钦宽.一类奇摄动非线性边值问题激波解的间接匹配［J］.华侨大学学报：自然科学版，2006，27（2）：123-125.

Singular Perturbation of Second Order Quasilinear Boundary Value Problem with Turning Point

XU Guo-an1，YU Zan-ping2
（1.School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China；2.School of Mathematics and Computer Science，Fujian Normal University，Fuzhou 350007，China）

In this paper，we study the singularly perturbation of second order quasilinear boundary value problem with turning point.Under the lost of weakness stability，using the method of upper and lower solution，we prove the existence of solutions and get the uniformly valid asymptotic estimation of solutions.

turning point；boundary value problem；singular perturbation；seand order quasilinear

O 175.1

A

1000-5013（2010）03-0346-05

（责任编辑：陈志贤 英文审校：张金顺，黄心中）

2009-05-19

许国安（1981-），男，讲师，主要从事微分方程奇异摄动理论的研究.E-mail：xga99163@163.com.

国务院侨办科研基金资助项目（07QZR09，09QZR10）