冲击负荷下发电机端部磁场及绕组振动分析*
刘明丹, 许丽佳, 康志亮
(四川农业大学信息与工程技术学院,四川雅安 625014)
0 引言
汽轮发电机受到冲击负荷时,端部磁场密度大大高于正常负载运行时的磁密,由电动力引起的端部绕组振动也随之增大。当这种振动超过一定限幅时,就会造成绕组的机械损伤或者造成绕组的机械疲劳,成为事故的诱因。单纯依靠加大汽轮发电机组端部绕组的支撑结构强度和数目,虽然可以解决端部绕组电动力所引起的绕组机械损伤问题,提高发电机运行的可靠性,但同时也带来了材料利用率低、电机造价偏高、制造难度增加等不利因素。准确计算汽轮发电机在不同工况下(包括最严重的事故状态下)端部绕组所受到的电动力,以及由此产生的振动,对合理选择端部材料、优化端部结构设计、降低发电机制造成本等具有重要意义。对已经投入运行的发电机组,端部绕组电动力和振动分析也可起到改进端部结构、估测端部绕组振动情况、避免事故发生等作用。
1 端部绕组电动力的计算
1.1 电动力计算的基本公式
在对端部定子绕组的振动进行分析计算之前,必须准确地求出端部绕组受到的电动力。由洛仑磁力的公式,可以推导出:
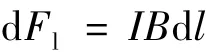
所以,流过电流I的导线元dl在电磁场中受到的力密度可以表示为

式中:f——导线元dl受到的力密度;
I——导体中流过的电流,用导线元的方向作为I的方向;
B——导线元dl处的磁通密度。
在圆柱坐标系中,式(1)可以表示为[1]
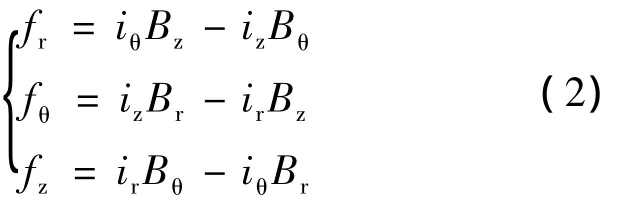
1.2 绕组电动力的计算
一般情况下,绕组由于受到电动力而产生的振动形变非常微小,可以忽略不计。因此,计算端部绕组电动力时,不考虑绕组的变形,将端部绕组的渐开线部分近似简化成直线段。
当求出t时刻发电机端部子午面上的磁场分布后,整个端部磁场的空间分布也随之确定。先将定子端部绕组分成若干直线段,求出每段绕组导体中点处的磁通密度,导体所在的相带决定了t时刻绕组中电流的大小,这样就利用式(2)求出了端部绕组上的力密度分布,再应用数值积分的方法求出端部绕组在t时刻受到的电动力大小。
2 发电机定子绕组端部振动的分析
2.1 基本假设
对发电机定子绕组端部进行振动分析时,要对其作如下假设:(1)假设端部定子绕组由线性弹性和连续分布的材料构成;(2)假设定子绕组构成材料具有均质性和各向同性;(3)假设振动时定子绕组的变形量比绕组的尺寸小很多,可以忽略振动时外力位置的改变;(4)假设材料符合广义虎克定律,即变形与外力呈线性关系。
由以上假设,可以将发电机定子绕组端部看作线性系统。线性系统一般服从叠加原理,即作用于结构上若干个荷载的综合效应等于各个荷载单独作用效应的总和。这样就可以运用叠加原理分别求出绕组各段上电动力所引起的振动,再合成出总的结果。
2.2 定子绕组振动的固有频率
发电机定子端部绕组是用若干绑定固定在端部支撑结构上的,相邻绑定之间的绕组可等效成一个具有两端简支边界条件的等截面梁,梁的简支端上挠度y与弯矩M等于零,即[7]:
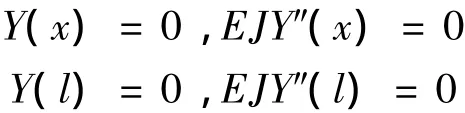
由端部绕组振动的数学模型可知,梁的固有
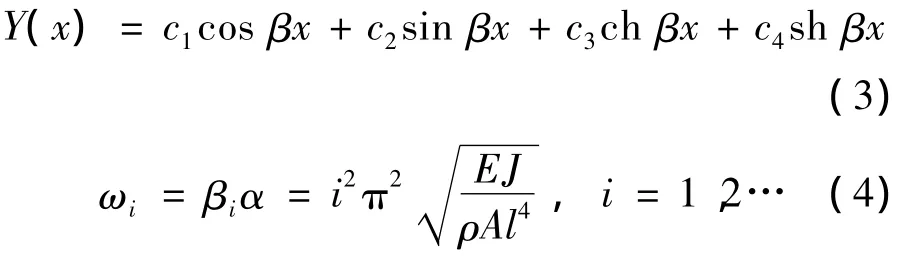
式中:E——材料的弹性模量;
J——截面对中性轴的惯性矩;
ρ——单位体积梁的质量;
A——梁的截面积;
l——梁的长度。
分析式(4)可知,定子绕组振动的固有频率与材料的性质、截面积及相邻绑定的距离有关。为了避免绕组发生共振现象,可以用改变上述几个参数的方法来改变绕组振动的固有频率。
2.3 定子绕组横向强迫振动分析
假定端部绕组是一个线性系统,它满足叠加原理,当梁振动时[8]:振动主振型和定子绕组的固有频率分别为
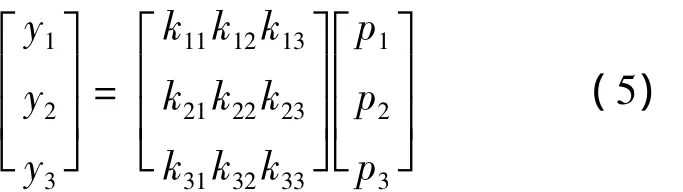
或:
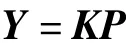
式中:yi——梁在i处的挠度(i=1,2,…);
kij——系统在j处受到单位力作用时对应于处产生的位移;
pi——梁在i处受到的作用力。
现以一段绕组为例,说明矩阵K的求法。假设一段长度为l的绕组被平分为4段,在每一段绕组的中心点处受到大小为pi(i=1、2、3、4)的作用力,每一段绕组的中心点分别表示为第一、二、三、四点,它们距离绕组左端的距离分别为l/8、3l/8、5l/8、7l/8。这样,在第一点处作用单位外力时,第一点处的挠度为[10]
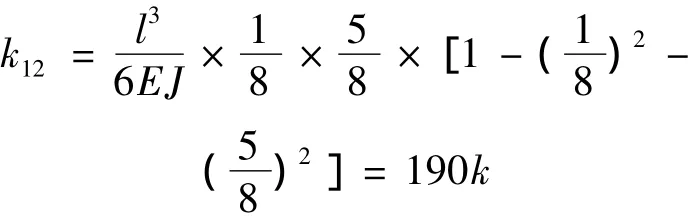
其中:k=l3/(24 567EJ),同样可以求出矩阵K中其他各元素的表达式。
3 端部绕组电动力和振动的计算
本文对一台320 MW汽轮发电机作实例计算。
3.1 端部磁场瞬态分布计算
首先对冲击负荷工况下该发电机端部电磁场的瞬态分布进行计算。图1为t=24.28 s和t=24.29 s时,发电机端部磁场分布图。从图1可看出,由于定子电流的波动,该计算点的磁感应强度约在24.28 s时有一个很大的波动。
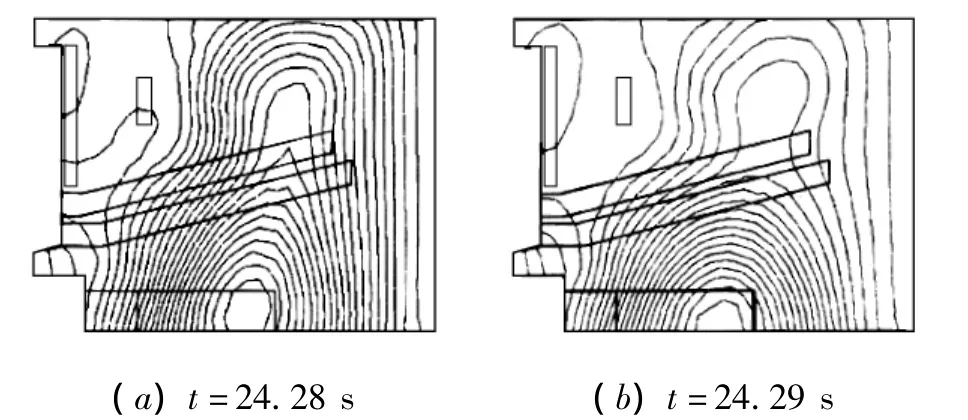
图1 t=24.28 s和t=24.29 s时,发电机端部磁场分布图
3.2 绕组振动固有频率的计算
表1为采用不同绑定距离时,绕组振动固有频率比较。影响绕组电动力最重要的因素是绕组电流,受到最大电动力的绕组一般位于电流值最大的相带,这反映出磁场旋转对绕组电动力的影响。
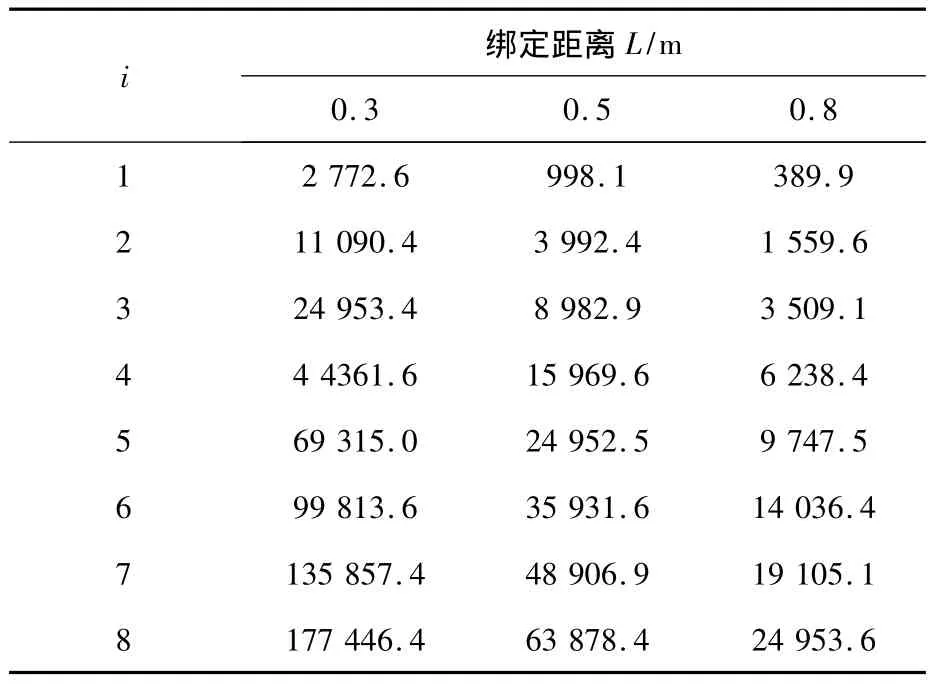
表1 不同绑定距离时,绕组振动固有频率的比较
为了避免绕组运行时发生共振现象,需要将绕组振动的固有频率避开工频及其倍数频率。通过上面的计算可知:改变绑定之间的距离可以改变绕组的固有振动频率,而且距离较短时,绕组的固有频率较高。
3.3 绕组端部的振动计算
在前文端部电磁场分布和绕组电动力密度计算的基础上,对冲击负荷下发电机端部绕组的振动情况进行了计算。图2为绕组的第27段、第32段和第22段在冲击负荷发生后,振动位移随时间变化的曲线。这三段都位于相邻两个绑定中间的位置,振动幅度较大。从图2可以看出,在24、28 s之后,三段绕组的振动位移都达到了最大值,这是由电流发生了较大波动而引起的。从振动位移的最大值来看,位于上层绕组的第27段和第32段分别是28.526 μm 和27.449 μm,而位于下层绕组的第22段的最大位移是9.392 μm。可见上层绕组振动的振幅要比下层绕组大很多。
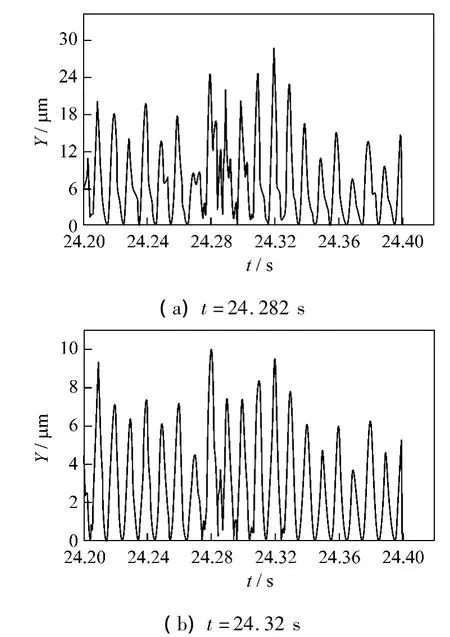
图2 冲击负荷下,t=24.282 s和t=24.32 s时端部绕组的振动
从图2可以看出,上层绕组的振动比下层绕组要大许多。另外在上层绕组或下层绕组中,绕组靠近鼻端部分的振动要比绕组的直线部分大许多。这与实际运行中发生的情况相吻合。
如果绕组长期处于这种振动中,若造成了端部绕组固定结构的松动,则会严重加剧绕组的振动。图3所示为假定上层绕组靠近鼻端的一个绑定松动后,t=24.32 s时端部绕组的振动情况和上层绕组第30段绕组振动位移随时间变化情况。
可以看出,由于短路情况使绑定松动后,上层绕组的振动位移比正常情况下大很多。如在t=24.32 s时,上层绕组振动最严重的第30段位移为267.8 μm,而在正常情况下,上层绕组振动最严重的第27段位移为28.526 μm,仅为前者的10.6%。由此可见,发电机端部的定子绕组固定部件非常重要,一旦发生松动、脱落等现象,将导致定子绕组振动的加剧。
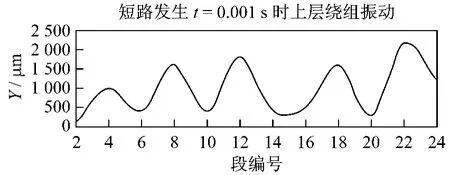
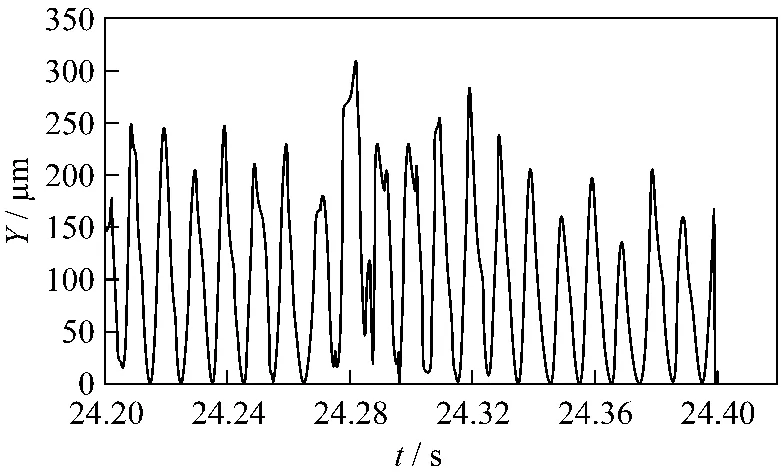
图3 绑定松动情况下,t=24.32 s时端部绕组的振动和位移情况
4 结语
计算结果和分析表明:端部绕组上各段振动幅度大小与该段绕组上分布的电动力密度有关,也与该段绕组位置有关;同一时刻,由于磁感应强度不同,导致上层绕组的振动幅度比下层绕组的振动幅度大;绕组靠近鼻端部分振动的振幅比绕组直线部分要大,这是由电动力密度分布不同而造成的;通过改善端部绕组绑定的位置,可以合理减小最大振幅,使得振幅的分布更加均匀。
[1]杨苹,吴捷,冯永新.200 MW汽轮发电机组振动故障的模糊诊断系统[J].电力系统自动化,2001,25(10):45-49.
[2]董溯新.水轮发电机振动[M].北京:清华大学出版社,2001.
[3]Nicola Lambert,David A K ,Rognon J P.A piezoelectric motor using flexural vibration of a thin piezoelectric membrane[J].IEEE,Transaction on Ultrasonic,Errol electrics and Frequency Control,2000,45(1):23-29.
[4]庄表中,黄志强.振动分析基础[M].北京:科学出版社,2002.
[5]黄学良,胡敏强,赵家壁.汽轮发电机端部似稳涡流场数学模型[J].东南大学学报,1995,25(2):90-97.
[6]李骊.强非线性振动系统的定性理论与定量方法[M].北京:科学出版社,2000.
[7]邱家俊.电机的机电耦联与磁固耦合非线性振动研究[J].中国电机工程学报,2002,22(5):109-115.
[8]Senske.汽轮发电机定子绕组端部电气故障时的振动形态[J].国外大电机,2001(2):25-33.
[9]曲大庄.汽轮发电机定子绕组端部振动固有频率计算的有限元方法[J].大电机技术,1988(5):30-38.
[10]Fuchs H.用于大型汽轮发电机定子绕组固定部件的玻璃纤维增强塑料[J].国外大电机,1994(2):52-62.
[11]史进渊,杨宇,孙庆,等.大型汽轮发电机故障特征规律的研究[J].中国电机工程学报,2000,20(7):35-44.

