现场可编程门阵列在开关磁阻电机无传感器位置检测中的应用
纪艳华, 陈 亮
(1.江苏大学电气信息工程学院,江苏镇江 212013;
2.上海电器科学研究所(集团)有限公司,上海 200063)
0 引言
开关磁阻电机调速系统是由双凸极开关磁阻电动机(Switched Reluctance Motor,SRM)、功率变换器、控制器及检测器等组成的一种新型电动机调速系统(见图1)。与传统的直流和交流调速系统相比,SRM不仅保持了异步电动机的全部优点,而且电机结构简单、控制方便、运行可靠、成本低、效率高,正获得日益广泛的应用。SRM的转子位置检测是SRM正常运转的重要组成部分,其检测方案分为直接位置检测法和间接位置检测法两类。直接检测法引入了位置传感器,使得电机结构变得复杂,安装也不方便,还使得SRM调速系统的可靠性下降。因此,间接位置检测技术正逐渐成为SRM调速系统研究的热门课题。
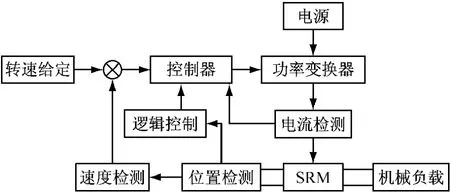
图1 SRM调速系统的基本组成
无位置传感器检测方法很多,如电流波形监测法、状态观测器检测法、磁链法、利用相间互感与转子位置关系检测、电容式位置检测技术、加测试线圈检测等方案,这些方案各有优缺点,但综观其实际效果却有一个共同的不足之处就是这些算法往往比较复杂,对位置检测的实时性要求较高,因此目前只局限在中低速领域。
本文在6/4极SRM单相轮流导通和电流采用脉宽调制(Pulse Width Modulation,PWM)技术控制的条件下,利用现场可编程门阵列(Field Programmable Gate Array,FPGA)实现磁链法的间接位置检测方案。将表示电流-磁链-位置角关系的励磁特性曲线放入查找表中,不仅节约了大量的运算时间,而且在高速区仍能获得准确可靠的位置信号。
1 磁链法的基本原理及算法
1.1 基本原理
磁链法直接对激励相绕组的电流进行检测,从而得到转子位置信号。根据SRM的一相电压方程:
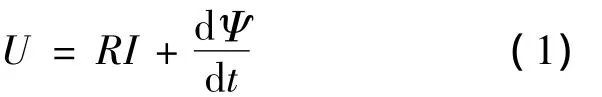
得到一相绕组的磁链表达式:
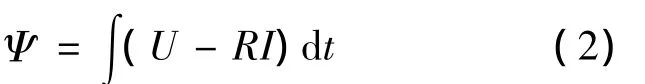
测量出电机激励相的电流I和电压U及定子电阻R,即可计算出某一时刻的定子磁链值。实际电机转子位置θ、定子磁链Ψ和电流i的关系如图2所示。
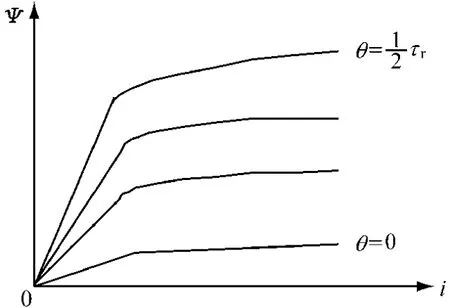
图2 SRM励磁特性曲线
SRM的励磁特性曲线可以通过实际测量或有限元分析的方法得到,制成表格,在电机运行时通过查表,实时地得到转子的位置。
1.2 算法简述
大多数位置估算算法并不考虑起动时的情况,本文为了实现SRM的无迟滞起动,需要在没有对转子初始校准和无干扰的情况下开始获得转子位置信息,因此算法中包括起动时的转子位置估算,具体算法如下(流程如图3所示):
(1)在短时间内(0.5 ms)给电机的所有相通电;
(2)测量所有相的电压和电流;
(3)获取最大电流相(励磁相);
(4)计算该相的磁链值;
(5)根据电流和磁链值查励磁特性表,估计转子位置;
(6)再转到步骤(2)。
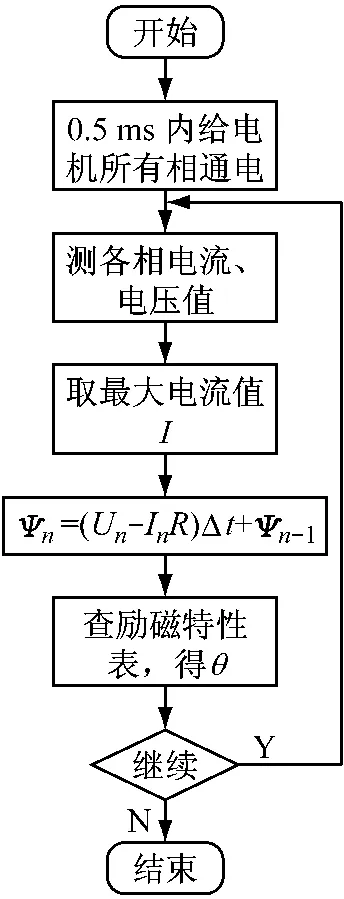
图3 磁链法估算转子位置流程图
2 基于FPGA的位置检测控制器
FPGA芯片作为数字控制器用于实现无传感器位置检测时,其输入、输出信号如图4所示。由电流和电压传感器检测到的三相绕组电压、电流值信号需经过八选一的多路选择开关,开关的输出连接到八位A/D转换器,从而将模拟信号转变成数字信号传送给数字控制器。图5所示为数字控制器内部的结构框图。
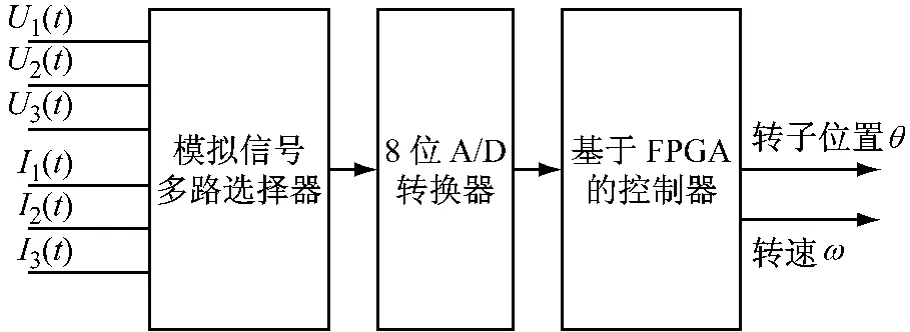
图4 控制器输入输出原理图
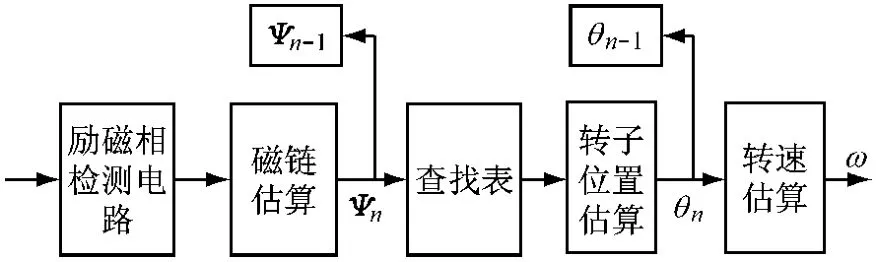
图5 基于FPGA的数字控制器结构框图
2.1 励磁相检测电路
励磁相检测电路用于确定电机起动时给哪一相绕组通电。因为励磁相的气隙阻抗相对较大,电感较小,所以当短时间激发所有相时,检测到的励磁相电流应该最大。励磁相检测电路的原理是利用一个简单的电流比较器,比较输入的三相电流的大小,并输出最大电流相的电流值,输出的电流值再作为磁链估算电路的输入。
2.2 磁链估算电路
本文中磁链的估算采用递归算法,即根据第n个周期的电流和电压值以及第n-1周期的磁链,计算出第n个周期的磁链。
将式(2)离散化可得:
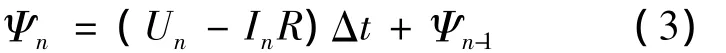
式中:Δt——离散积分磁链的计算周期;
Un、In——第n个离散周期里绕组的电压、电流值;
R——相绕组电阻,可假设为常数;
Ψn-1——第n-1周期的磁链,在电机刚刚起动时,可以认为此时的Ψn-1为零。
2.3 查找表
查找表中存放的是磁链、电流和转子位置的值,也就是电机的励磁特性曲线所反映的内容。通过试验实际测量或者通过仿真软件Ansoft/Maxwell 2D用有限元分析的方法可以得到6/4极SRM在不同转子位置时的磁链和电流值,从而得到电机转子位置θ、定子磁链Ψ和电流i的关系,将其制成表格,即得到查找表。
由于试验和仿真软件得到的磁链值都是小数的形式,为了能够在FPGA中用十六进制的形式表示这些小数,还必须将这些小数进行适当的尺度变换。
2.4 转子位置估算电路
根据式(3)计算得到的磁链值与当前的绕组采样电流一起,在电机运行时通过查找表可以及时准确地得到当前转子的位置。通过查表获得的转子位置信息可以有效地用于控制SRM相绕组电流的开通与关断。
2.5 转速估算电路
第n个周期内的转速ωn可由式(4)计算得到:
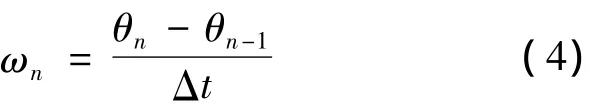
式中:θn,θn-1——从转子位置估算电路获得的第n个周期和第n-1个周期的转子位置角度值。
3 仿真与结果分析
本文选用一台三相6/4极SRM为对象,其中R=0.5 Ω,Lmin=8 mH,Lmax=60 mH。对电机电流采用PWM控制,转速环采用模糊控制策略,使用MATLAB/Simulink仿真软件对所设计的无位置传感器的SRM调速系统进行仿真。
图6给出了基于电流PWM控制下的瞬时一相电流波形,图7为系统的速度响应曲线。
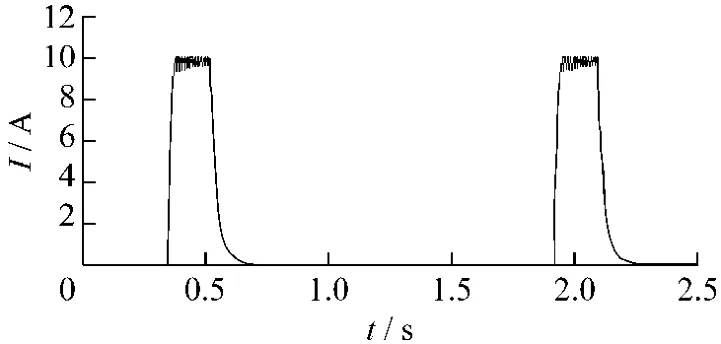
图6 瞬时电流跟踪下的一相电流波形
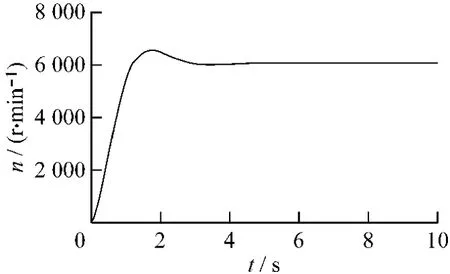
图7 速度响应曲线
图6、7表明所设计的基于FPGA的数字控制器,不仅可以实现电流斩波控制,而且整个调速系统可以取得超调小、响应速度快、无静差这样比较好的调速性能。
4 结语
本文提出了一种借助VHDL语言将FPGA用于无位置传感器的位置检测方法,详细阐述了控制器的结构及其设计思想,并通过仿真证实了该算法可以实现SRM任何位置下的无迟滞起动,并准确估算了转子位置。
如何借助VHDL语言用一片FPGA芯片实现整个数字控制器的功能,将是今后研究的重点和难点。这一技术的实现不仅可以使控制器节省空间,更可以提高控制的速度和精度,从而拓宽无位置传感器SRM的实用领域。
[1]王宏华.开关磁阻电机调速控制技术[M].北京:机械工业出版社,1995.
[2]王宏华,许大中.开关型磁阻电动机转子位置检测技术[J].电工电能新技术,1996(3):48-53.
[3]刘剑,刘素娟.开关磁阻电机无位置传感技术研究[J].中小型电机,1998,25(4):16-19.
[4]王大方,谢依顺.无位置传感器开关磁阻电机的转子位置检测与启动[J].海军工程大学学报,2004(3):36-39.
[5]Fahimi B,Suresh G,Ehsani M.Review of sensorless control methods in switched reluctance motor[C]∥Industry Applications Conference,2000:1850-1857.
[6]Gao H,Salmasi F R,Ehsani M.Sensorless control of SRM at standstill[C]∥Applied Power Electronics Conference and Exposition,2001:850-856.

