一种基于LMS的改进变步长算法及其应用

张 辉，李 竹，崔大鹏，行小帅，行 宙

（山西师范大学物理与信息工程学院，山西 临汾 041004）

一种基于LMS的改进变步长算法及其应用

张 辉，李 竹，崔大鹏，行小帅*，行 宙

（山西师范大学物理与信息工程学院，山西 临汾 041004）

在分析定步长LMS算法和变步长LMS算法的基础上，提出了一种改进的LMS算法，改进的LMS算法是利用瞬时误差的绝对值的三次方和遗忘因子共同来调整步长的.理论分析和系统辨识的仿真结果均表明，新算法确实具有更快的收敛速度.

LMS算法；变步长；遗忘因子；系统辨识

在系统辨识、噪声消除、自动控制等工程技术领域，广泛应用了一种最小均方误差LMS（Least Mean Squre）算法，它是由Widrow和Hoff提出的，其最大的优点就在于结构简单、稳定性好、计算量小、易于实现.LMS的指导思想是随着迭代次数的增加，不断改变滤波器抽头权向量，从而使实际输出y（n）不断地接近理想输出d（n），使y（n）与d（n）之间的误差小于某个设定的较小值.然而，研究表明，传统LMS算法［1-2］（又称FSS-LMS算法）存在着收敛速度和稳定性之间的固有矛盾，为了解决这一矛盾，最流行的算法就是采用变步长LMS算法（又称VSS-LMS算法）.目前人们已经研究出了一些变步长算法，尽管它们的原理不同，但其基本指导思想是一致的，都是在算法不同的收敛时刻，采用不同的步长μ值来平衡收敛速度和稳定性.例如，文献[3-5]都分别提出了不同的变步长LMS算法.本文在分析FSS-LMS算法和VSS-LMS算法的基础上，提出了一种新的变步长LMS算法，即NVSS-LMS算法，它的步长是由瞬时误差的绝对值的三次方和遗忘因子共同来调整的.

1 传统LMS算法和普通变步长LMS算法

传统LMS算法包含以下几个关系：

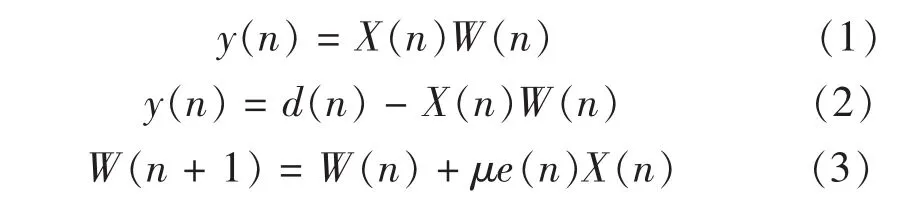
式中，d（n）为理想输出信号，X（n）为输入信号向量，W（n）为滤波器的抽头权向量，e（n）为误差信号，μ为步长参数，它决定抽头权向量在每步迭代中的变化量，是影响算法收敛速度的重要参数［3-7］.因此，步长参数μ在LMS算法中起到极为重要的作用.研究表明，μ值较大时收敛速度较快，而稳定性较差；μ值较小时，收敛速度较慢，却可以提高稳定性.所以在传统LMS算法中，由于μ为一个常数，当随机输入一个信号向量X（n）时，μ的取值总会造成收敛性和稳定性之间的矛盾.为了解决传统LMS固有的这种矛盾，文献[3]探索了变步长LMS算法，其指导思想是：在算法初始收敛阶段μ较大，以便有较快的收敛速度，当算法收敛后，μ较小，以便有较好的稳定性，μ是一个随着迭代次数变化而变化的量.

文献[3]提出的变步长LMS算法，其核心公式见式（4）和（5）.

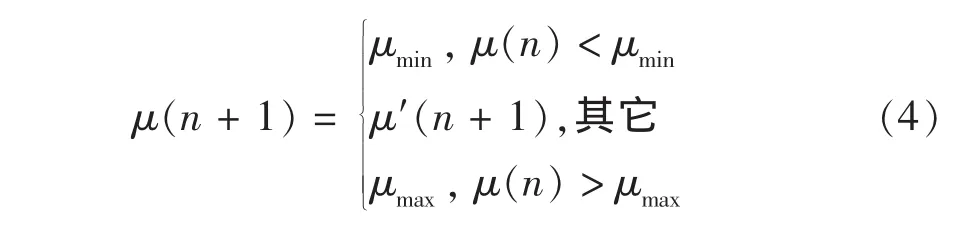
式中

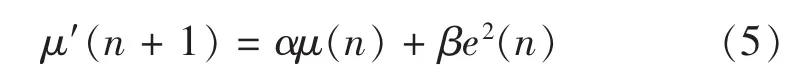
μmin为具有跟踪能力的最小步长，μmax为获得最大收敛速度的步长，α为步长的遗传因子，决定本次迭代时μ（n+1）受上一次迭代时μ（n）的影响程度；β决定步长受误差e（n）的影响程度，一般取值较小.在算法收敛的初始阶段，由于e（n）较大，所以μ（n+1）较大，则收敛速度较快；当算法即将达到收敛时，e（n）较小，所以μ（n+1）也较小，则算法有较好的稳定性.这样就较好地解决了传统LMS算法中μ取固定值而带来的收敛性和稳定性之间的矛盾.

2 新的变步长LMS算法（Modified variable step size LMS algorithm）

通过对文献[3，5，7]变步长算法的分析研究，本文提出了一种新的变步长LMS算法，此算法是通过误差积累来调节步长参数，其核心表达式见式（6），（7）和（8）.

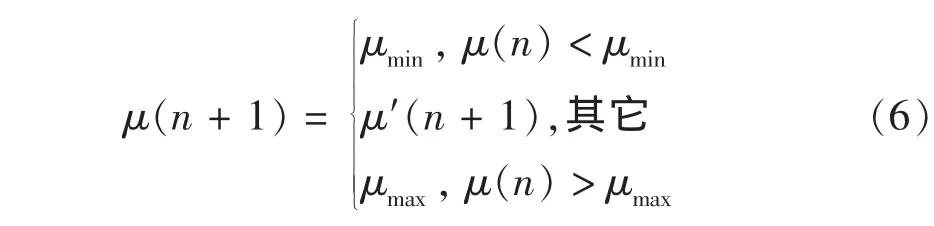
式中

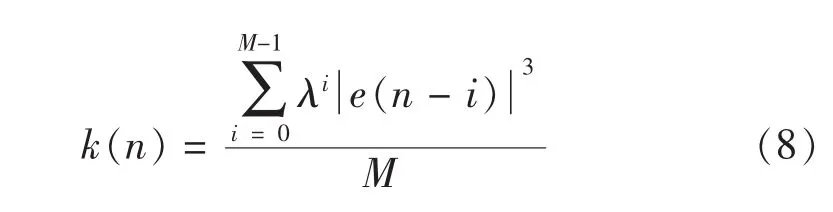
其中，λ是步长参数调节量的遗忘因子，且0＜λ＜1，λ取值接近于1；α和β的取值和意义同文献[3]中变步长LMS.

3 算法在实际应用中的比较

3.1 系统辨识

系统辨识是现代控制理论中的一个分支，凡是需要通过实验数据确定数学模型和估计参数的场合都要利用辨识技术，辨识技术已推广到工程和非工程的许多领域，如化工过程、核反应堆、电力系统、航空航天飞行器、社会经济系统等.其主要思想就是利用未知系统的输入输出数据，通过自适应系统，来辨别出未知系统的数学函数模型及特性.其基本原理框图见图1.

图1 系统辩识框架Fig.1 SysteMldentification Diagram

由图1可以看出，系统输入为随机信号xin（n）和白噪声v（n）混合得到未知系统的输入，未知系统为8阶横向滤波器，假设自适应滤波器阶级与未知系统相同，d（n）为对未知系统测量所得到的信号，y（n）为对未知系统输出信号的估计，它和测量信号的差值就是误差信号e（n），系统辨识就是依靠误差信号e（n）来反馈调节自适应滤波器的权向量W（n），使之和未知系统吻合，误差信号μ（n）可表示为式（9）.

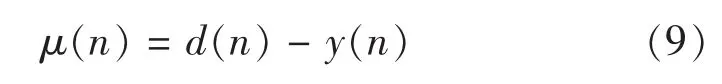
3.2 仿真实验

下面将传统LMS，变步长LMS，改进变步长LMS分别应用于系统辨识，通过计算机来仿真.实验时各参数设置如下：FSS-LMS的步长定为0.01，为了较好的比较VSS-LMS和NVSS-LMS两算法的性能，它们的参数设置相同，μmax=0.2，μmin=1×10-8，α=0.99，β=8×10-4，另外，NVSS-LMS对 NVSSLMS算法的 λ=0.99，M=4.每种算法分别作1000次独立实验，然后对其求平均，得到实验结果如图2和图3所示，在图中横轴表示迭代次数，纵轴表示抽头权值，可以看出两种算法的辨识结果均趋于理论值.

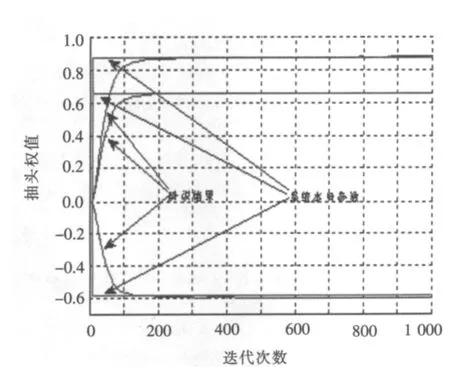
图2 VSS-LMS系统辩识结果Fig.2 SysteMidentification results by VSS-LMS

在图2和图3中，仿真的量是系统辨识中FIR滤波器的前3个系数，比较两种算法的实验结果可见，NVSS-LMS辨识的结果在迭代80次时就和系统一致，而VSS-LMS算法则需要迭代150次才和系统一致，显然NVSS-LMS算法辨识速率比VSSLMS算法要快得多.

跟踪性能是评价一种算法对非平稳环境的适应能力的重要指标，图4是NVSS-LMS算法和VSSLMS算法跟踪性能的比较，横轴代表迭代次数，纵轴代表均方误差，可以看出，在非平稳环境下，当系统的参数变化时，NVSS-LMS算法的收敛速度比VSS-LMS算法要快.

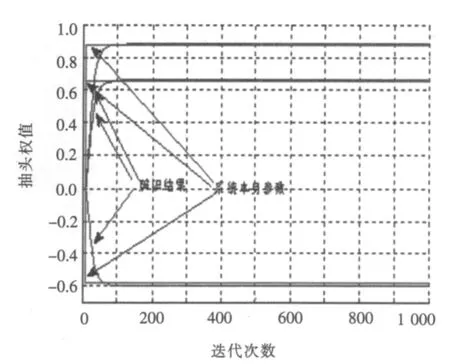
图3 NVSS-LMS系统辩识结果Fig.3 SysteMidentificatioMresults by NVSS-LMS

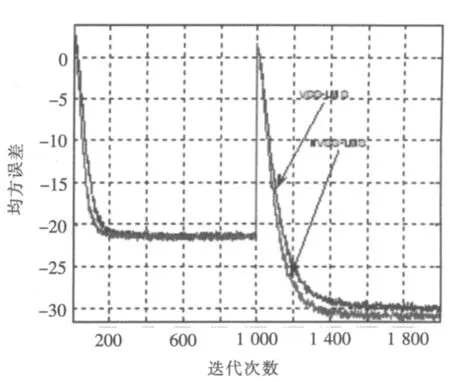
图4 NVSS-LMS和VSS-LMS跟踪性能的比较Fig.4 The contrast of tracking performance of NVSS-LMS and VSS-LMS

4 结论

本文所提出的改进变步长算法是利用瞬时误差的绝对值的三次方和遗忘因子共同来调整步长的.理论及实验结果均表明，与前两种算法相比，改进变步长算法的初始收敛阶段步长明显较大、收敛曲线较陡、系统辨识结果需要较少的迭代次数.因此说，本文提出的改进型LMS算法的性能确实优于前两种算法.

［1］WidroWB，Mccool J M，Arimoer MG.Stationary and no stationary learning characteristics of the LMS adaptive filter [J].Proc IEEE，1976，64（8）：1151-1162.

［2］Haykin S.Adaptive Fittering Theroy[M].Prentice Hall，Englewood Cliffs，NeWJersey，1986.

［3］Kwong R H，Johnston E W.A Variable Step Size LMS Algorithm[J].IEEE Trans.Signal Processing，1992，40（7）：1636-1642.

［4］Gitlin R D，Weinstein S D.The Effects of large Interference on the Tracking Capability Implemented Echo Cancellers[J].IEEE Trans on COM，1978，30（6）：833-839.

［5］Tyseer A，Mayyas K.A robust variable step-size LMSType algorithm：analysis and simulations[J].IEEE Trans on Signal Proc，1997，45（7）：631-639.

［6］Pazaitis D I，Constantinides A G.A novel kurtosis driven variable step-size adaptive algorithm[J].IEEE Trans Signal Processing，1999，47（3）：864-872.

［7］Hyun C S，Sayed A H，Woo J S.Variable Step-Size NLMS and Affine Projection Algorithms[J].IEEE Signal Processing Letters，2004，11（2）：132-135.

［8］Pei Binnan.On convergence and selecting step size for the LMS algorithm[J].Journal of China Institute of Communications，1994，15（4）：106-111.

A NeWLMS AlgorithMof Variable Step Size and Its Application in SysteMIdentification

ZHANG Hui，LI Zhu，CUI Dapeng，XING XiaoShuai*，XING Zhou
（School of Physics and Information Engineering，Shanxi Normal University，LinFen 041004，China）

This paper presented a neWLMS algorithMof variable step size after a brief discussion on traditional LMS and VSS-LMS algorithm，which controls step size according to the absolute value of third power of instantaneous error and forgetting factor.Theory analysis and computer simulations demonstrate that the presented algorithMhas faster convergence.

LMS algorithm；variable step size；forgetting factor；systeMidentification

TN 911.7

A

1674-4942（2010）01-0025-04

2009-11-28

山西省青年科技研究项目（20031008）

*通讯作者