关于构造三类奇数阶幻方的新方法
王辉丰,詹 森
(1.海南师范大学 数学与统计学院,海南 海口 571158;2.广东技术师范学院 计算机科学系,广东 广州510665)
关于构造三类奇数阶幻方的新方法
王辉丰1,詹 森2
(1.海南师范大学 数学与统计学院,海南 海口 571158;2.广东技术师范学院 计算机科学系,广东 广州510665)
给出构造奇数阶幻方、奇数阶对称幻方、奇数阶奇偶分开对称幻方的几种方法,并对后2种方法给出理论证明.还提出完美幻方的构造方法.
奇数阶;幻方;对称幻方;奇偶分开对称幻方;完美幻方;构造方法
我们研究了高阶幻方的构造方法[1-2],文[2]给出了构造奇数n=2m+1(m为m≠3s+1,s= 0,1,… 的自然数)阶对称完美幻方的基元顺安双移法(简称六字法).在这基础上,我们进一步运用推广这种六字法,又提出几种方法,可分别构造n= 2m+1(m=1,2,…)阶幻方和n=2m+1(m= 1,2,…)阶对称幻方、n=2m+1(m=1,2,…)阶奇偶分开对称幻方等三类幻方,并给出后2种方法的证明,最后提出了完美幻方的构造方法.其方法既简单又直接,容易操作.以下分4种类型进行论述.
1 n=2m+1(m=1,2,…)阶幻方的构造方法
第一步 将基数按如下方式安装到n阶基方阵A.
取定a(1,m+1)=mn+1,其余n-1个基数1,n+1,2n+1,…,(m-1)n+1,(m+1)n+1,…,(n-1)n+1,可任意安装到如下n-1个位置:
a(m+1-k,k+1)(k=0,1,2,…,m-1),
a(m+1+k,n-k+1)(k=1,2,…,m).
基数安装完毕后,得到基方阵A的全部基元(或站点)[2].接着,在每一列站点的下方,自上而下依顺序安装(称顺安)相连的数至该列最下面的笫n行;在该站点的上方,自上而下顺安后继的数,一直安装满全列为止,这样,经过基元顺安得到的n阶基方阵A的每一行数字之和都等于幻方常数.
第二步 对基方阵A施行顺移安装到另一个(待安装的)n阶方阵B.
把A中第一列每一行的数顺移至B中同一行相应于A的基元所在的位置,A中各行的其他元素顺移至B中.所得方阵B就是一个幻方.
这样,经过以上任安基元和顺安、顺移(称双顺)两步得到的就是一个n=2m+1(m=1,2,…)阶幻方.把这种安装方法称为任安基元双顺法,也简称六字法.
由于基数安装结构可有(n-1)!种不同的选择,而移入方式亦有其他可能的选择,所以,利用以上方法至少可构造出(n-1)!个不同的幻方.
2 n=2m+1(m=1,2,…)阶对称幻方的构造方法
第一步 由基元顺安基方阵.
对于n=2m+1(m=1,2,…),我们按文[2]的第一步(1)~(5)式安装基元和行标及其他元素到n阶方阵A中,得到基方阵A.为了避免重复,这里略去上述的式(1)~(5).
第二步 由基方阵施行双移安装可得另一个方阵.
设待安装的另一个n阶方阵为B,以b(i,j)(i,j=1,2,…,n)表示其位于第i行,第j列的元素,取

以行标a(m+1-k,1)(k=1,2,…,m)向右移动 k个位置,即

以行标a(m+1+k,1)(k=1,2,…,m)向右移动n-k个位置,即

式(2)、(3)就是完成了向右移动(注意这里的右移与文[2]右移位置(7)、(8)不同).此时已将A的笫一列的元素安装到B中.基方阵A的行标在方阵B中是式(2)、(3),也称它们为B的行标.注意b(m+1,1)=1既是B的基元又是行标,同一行中其余各元素按在A中的顺序进行顺移,A的基元在方阵B中是

其中r=r(2n-2k+1)为余函数[2].式(4)、(5)是B中的基元(与文[2](10)、(11)不同).
这样就安装了B的所有元素.按以上方法所得的方阵B就是对称幻方(见定理1).这种方法也称为基元顺安双移法,也简称六字法.
定理1 由上述六字法得到的n=2m+1(m= 1,2,…)阶方阵B是对称幻方.
证明 由文[2]的定理证明知,基方阵A的元素是中心对称的.自然其笫k行的元素与笫n-k+ 1(k=1,2,…,n)行的元素是关于中心对称的.即第m+1-k行的元素与第m+1+k(k=1,2,…,m)行的元素是关于中心对称的.双移不会改变两对称行对称元素的对称关系,事实上,双移时,方阵A第m+1-k行的元素向右顺移了k个位置;第m+1+k行的元素向右顺移了n-k个位置(即向左顺移了k个位置),这样,在方阵B中第M+1-k行的元素与第m+1+k(k=1,2,…,m)行的元素仍然是关于中心对称的.而中间一行自始至终不动,其对称性在方阵A中就已确定,所以,方阵B是中心对称的.
由文[2]的定理证明知,基方阵A任何一行元素之和都等于幻方常数.因为双移并不改变每一行的元素,所以,方阵B任何一行元素之和也都等于幻方常数.由于对称性,显然,对称方阵B对角线上元素之和等于幻方常数,因此,只要证明方阵B任何一列元素之和都等于幻方常数,定理就已得证.为此需要证明方阵B的n个行标,n个基元各自位于不同的n列上.
在安装方阵的过程中,显然,所得方阵B的n个行标位于不同的n列上.下面证明在B中的n个基元也位于不同的n列上.
对n=2m+1(m为自然数),由式(4)知,基元a(m+1-k,k+1)在方阵B的位置是b(m+1-k,2k+1)(仍是基元),当k=0,1,2,…,m时,有2k+1是一个1~2m+1的公差为2的等差有限数列.
由式(5)知,b(m+1+k,r(2n-2k+1))是在B中的基元,当k=1,2,…,m时,有
r(2n-2k+1)=(2n-2k+1)-n=n-2k+1是一个2~2m的公差为2的等差有限数列.
以上得到的数列1~2m+1和2~2m都是公差为2的等差有限数列,合并起来就是1~n的自然数,即n个基元位于B中的不同的n列上.由于方阵B的n个行标、n个基元位于不同的列上,由文[2]的定理证明知,方阵B任何一列元素之和都等于幻方常数.综上所述,方阵B是一个对称幻方.
由于方阵B关于中心对称的任何两行(或列)互换后仍然中心对称,互换后的方阵仍是一个对称幻方.所以用上述方法可得出2(m!)个不同的对称幻方.
3 n=2m+1(m=1,2,…)阶奇偶分开对称幻方的构造方法
第一步 与对称幻方的构造方法的第一步相同.所得方阵为A.
第二步 取定b(m+1,1)=a(m+1,1).行标a(m+1-k,1)(k=1,2,…,m),按以下方式向右移动:
当k为奇数时,

当k为偶数时,

行标a(m+1+k,1)(k=1,2,…,m),按以下方式向右移动:
当k为奇数时,
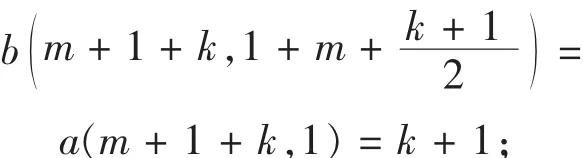
当k为偶数时,
基元a(m+1-k,k+1)(k=1,2,…,m)在方阵B的位置是:
当k为奇数时,
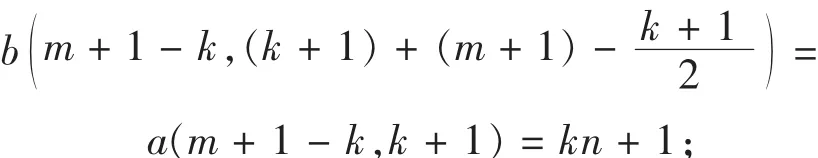
当k为偶数时,
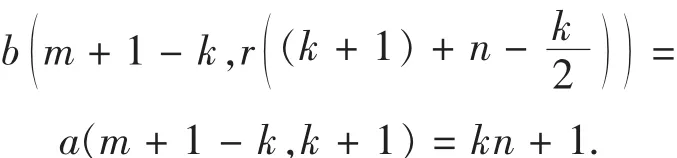
基元a(m+1+k,n-k+1)(k=1,2,…,m)在方阵B的位置是:
当k为奇数时,
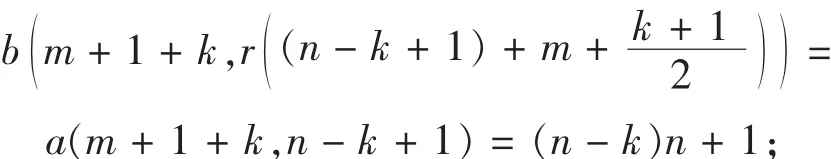
当k为偶数时,
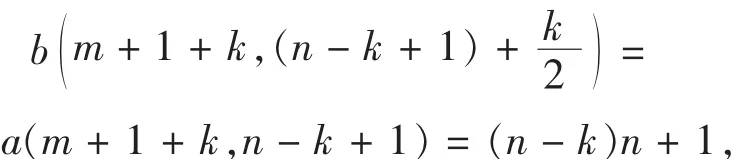
所得方阵为B.
第三步 作行变换安装到方阵C,使上面m+ 1行各行的行标由下至上依次为1,3,5,…,2m+ 1;使下面m行各行的行标由下至上依次为2,4,…,2m.
这样,所得的n=2m+1(m=1,2,…)阶方阵C就是一个奇偶数分开的对称幻方,简称奇偶分开对称幻方,这种方法称为基元顺安奇偶行变法,简称八字法.
定理2 由上述八字法得到的n=2m+1(m= 1,2,…)阶方阵C就是一个奇偶分开对称幻方.


注意到第m+1-k行与第m+1+k行的行标之和(n-k+1)+(k+1)=n+2,而方阵C处于对称位置上的任何两行,其行标之和都等于n+ 2,而中间一行自始至终不动,所以方阵C仍然是中心对称的.
由文[2]的定理证明知,基方阵A任何一行元素之和都等于幻方常数.因为双移或行变换并不改变每一行的元素,所以方阵C任何一行元素之和也都等于幻方常数.由于对称性,显然,对称方阵C对角线上元素之和等于幻方常数,所以只要证明方阵C任何一列元素之和等于幻方常数及奇数集中在方阵C中央的菱形内,而偶数则置于方阵的四个角,定理就已得证.为此首先需要证明方阵C的n个行标,n个基元各自位于不同的n列上.在安装方阵的过程中,显然所得方阵C的n个行标位于不同的n列上.下面证明在C中的n个基元也位于不同的n列上.
对n=2m+1=2(2t)+1,当k=1,3,…,2t-1时,基元

以上所得2~t+1的有限自然数列,t+2~2t+1的有限自然数列,2t+2~3t+1的有限自然数列,3t+2~4t+1的有限自然数列,合并起来就是2~n的自然数,而基元b(m+1,1)位于第一列,即n个基元位于方阵B中的不同的n列上.
对n=2m+1=2(2t+1)+1,同理可证n个基元位于方阵B中的不同的n列上.所以,对n= 2m+1(m=1,2,…),方阵B中的n个基元位于方阵B中的不同的n列上.
由于方阵B的n个行标、n个基元位于不同的n列上,由文[2]的定理1证明知,方阵B任何一列元素之和都等于幻方常数.综上所述,方阵B是一个对称幻方.由于行变换并不改变每一列的元素,所以,方阵C任何一列元素之和也都等于幻方常数.因此,方阵C是一个对称幻方.
对n=2m+1(m=1,2,…)阶方阵,由于基数列1,n+1,2n+1,…,(n-1)n+1是奇偶数的个数相间以及基数列和其他元素的安装方式,显然,当行标 k为奇数时,其所在行有(n+1)-k个元素是奇数,且奇数紧邻于行标之右;当行标k为偶数时,其所在行有k-1个元素是奇数,且奇数紧邻于行标之左(紧邻于第一列之左的是最后一列).作行变换使上面m+1行各行的行标由下至上依次为1,3,5,…,2m+1;使下面m行各行的行标由下至上依次为2,4,…,2m.奇数就集中于所得方阵C中央的菱形内而偶数则位于方阵C的4个角.至此已证得方阵C就是一个奇偶分开对称幻方.
4 完美幻方的构造方法
对于n=2m+1(m为m≠3s+1,s=0,1,…的自然数),若要直接构造一个n阶完美幻方,有许多种不同的安装基元的方式,比如取

但仍嫌不够简单.最直接的方法是,若用4个同样的n=2m+1(m为m≠3s+1,s=0,1,2,…的自然数)阶对称完美幻方,组成一个2n阶方阵,则在这个方阵中,以1~n2中任何一个数为中心,都可框出一个n阶完美幻方,即一个n阶对称完美幻方可产生n2个完全不同的n阶完美幻方(包括作为基础的那个n阶对称完美幻方).
注记 本文所提出的方法已包括了以下4种方法[3-4]:
1)把所得到的奇偶分开对称幻方,顺时針方向旋转90°,即可得出菱形法的结果.
2)把我们所得的对称幻方,顺时針方向旋转90°,再向左(或右)翻转180°,即可得出连续摆数法的结果.
3)把“任安基元双顺法”稍为推广一下,基数的安装改为
a(m+1-k,2k+1)=kn+1(k=0,1,…,m),
a(m+1+k,n-2k+1)=
(n-k)n+1(k=1,2,…,m).
安装基方阵A后,其行标按以下方式右移:
b(m+1-k,m+1-k+1)=a(m+1-k,1)(k=0,1,…,m),
b(m+1+k,m+1+k+1)=a(m+1+k,1)
(k=1,2,…,m-1),
b(n,1)=a(n,1).
所在各行的其他元素向右顺移,所得方阵B已是一个幻方,向上翻转180°,就得到阶梯法所得出的结果.
4)再将第3)的结果按顺时针方向旋转90°,就是拉伊尔法(就奇数阶幻方而言)所得出的结果.
[1]詹森,王辉丰.关于构造高阶幻方的新方法[J].海南师范大学学报:自然科学版,2009,22(3):250-254.
[2]詹森,王辉丰.奇数阶对称完美幻方的构造方法[J].海南师范大学学报:自然科学版,2009,22(4):396-402.
[3]詹森.关于构造幻方的新方法 [J].海南师范大学学报:自然科学版,2009,22(2):131-132.
[4]吴鹤龄.幻方及其他[M].北京:科学出版社,2004:50-80.
责任编辑:黄 澜
参考文献
[1]WidroWB,Mccool J M,Arimoer MG.Stationary and no stationary learning characteristics of the LMS adaptive filter [J].Proc IEEE,1976,64(8):1151-1162.
[2]Haykin S.Adaptive Fittering Theroy[M].Prentice Hall,Englewood Cliffs,NeWJersey,1986.
[3]Kwong R H,Johnston E W.A Variable Step Size LMS Algorithm[J].IEEE Trans.Signal Processing,1992,40(7):1636-1642.
[4]Gitlin R D,Weinstein S D.The Effects of large Interference on the Tracking Capability Implemented Echo Cancellers[J].IEEE Trans on COM,1978,30(6):833-839.
[5]Tyseer A,Mayyas K.A robust variable step-size LMSType algorithm:analysis and simulations[J].IEEE Trans on Signal Proc,1997,45(7):631-639.
[6]Pazaitis D I,Constantinides A G.A novel kurtosis driven variable step-size adaptive algorithm[J].IEEE Trans Signal Processing,1999,47(3):864-872.
[7]Hyun C S,Sayed A H,Woo J S.Variable Step-Size NLMS and Affine Projection Algorithms[J].IEEE Signal Processing Letters,2004,11(2):132-135.
[8]Pei Binnan.On convergence and selecting step size for the LMS algorithm[J].Journal of China Institute of Communications,1994,15(4):106-111.
责任编辑:毕和平
The NeWStructure Methods of Three Types of Odd Order Magic Square
WANG Huifeng1,ZHAN Sen2
(1.College of Mathematics and Statistics,Hainan Normal University,Haikou 571158,China;
2.Department of Computer Science,Guangdong Technical Normal University,Guangdong 510665,China)
Three neWstructure methods about odd order magic square,odd order symmetrical magic square and odd order symmetrical magic square with odd number and even number separated were qiven,the final two methods were theoretical proved and structure methods of perfect magic square were put forward.
odd order;magic square;symmetrical magic square;odd order symmetrical magic square with odd number and even number is separated;perfect magic square;structure method
O 157.6
A
1674-4942(2010)01-0012-04
2009-11-20

