相位测量轮廓术中一种有效补偿相移误差的新算法

朱 林 达飞鹏 盖绍彦

(东南大学自动化研究所，南京 210096)

(东南大学复杂工程系统测量与控制教育部重点实验室，南京 210096)

相移干涉术作为一种干涉计量的方法，由于它的测量精度高且实验易于实现，已经得到了广泛的应用.但其测量精度受到很多误差源的影响，影响相移干涉术的因素主要包括:相移机构的相移误差、光场的非正弦性误差、探测器的非线性误差等.为了获得较好的位相测量精度，减小测量误差，目前已有多人针对这一问题作了一系列的研究和探讨，给出了许多误差补偿算法.国外方面Morgan［1］提出了最小二乘拟合相位提取方法，Greivenkamp［2］促进了该技术的发展，给出了一些通用的算法.Frenchlad和 Koliopoulos［3］的贡献是应用傅里叶变换在频域上分析相位的提取，使得在设计算法和分析移相干涉测量误差方面有了很有效的分析工具.为了解决失谐误差的问题，Schwider等［4］做了很多工作，先后设计了Schwider－Hariharan五步算法和校正的四步相位算法，改进的算法使得微小失谐误差影响有所减小，其中尤以Surrel［5］提出的运用特征多项式分析和设计相移算法的方法最为典型.国内的研究人员惠梅等［6］也拓展思路，在用多项式构造相位提取的算法方面做了初步尝试，在提高准确度方面文献［7－8］对相位提取算法对误差的影响也进行了较详细的探讨.目前普遍求取相移误差的方法都是以单个相位点为研究对象［9－10］，进行误差求取.

本文提出了一种新的相移误差求取算法，利用了正弦投影条纹中相邻像素点间相位差的相等性这种特点，以相邻三个相位点为研究对象，提取相移误差，将求取出的相移误差代入到四步相移的相位计算公式中进行误差补偿，从而有效抑制了相移误差对相位计算的影响，最后用仿真结果验证了这种误差补偿算法的正确性.

1 相移干涉术经典模型原理分析

图1描述的是经典的相位法轮廓测量系统模型.

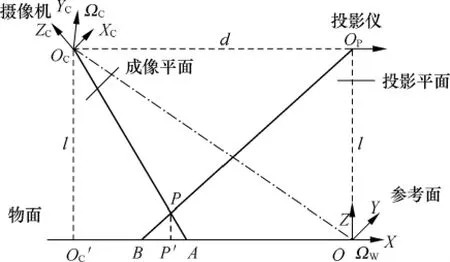
图1 经典相位法测量系统原理图

图中，OP为投影装置镜头光心，又称投影中心.OP在参考面上的投影为O.参考面又称虚拟面，即图中的OXY平面.该面平行于投影面，Y轴平行于投影面上光栅条纹方向，原点O即OP在本面上的投影.在传统相位法中，需要将标定工作面设置在此位置，来获得系统标定和测量时的基准相位值.故此面又称基准面.Ωw为参考坐标系OXYZ.以参考面为本坐标系的OXY平面.Ωc为摄像机坐标系OcXcYcZc，原点Oc位于镜头光心.Zc位于光轴，Xc，Yc分别平行于摄像机成像面的横轴，纵轴.OcOP连线平行于参考面.Oc在参考面上的投影为O′c.d为投影中心OP到摄像机光心Oc之间距离.l为OP到参考面之间距离.由于OcOP连线平行于参考面.也是Oc到参考面之间距离.P为物点，在参考面上的投影为P′.

相位法中，通常采用相移法［2，7］从摄像机拍摄的光栅条纹图像中提取相位场定量的分布.以常用的4幅图相移法为例，相移法的原理如下:

通过精确移动投影光栅，使光栅条纹图像的相位场移相［11］，得到4幅条纹图像，各图像可表示为

式中，i表示第i次相移;Ii为第i幅相移图上(x，y)点的灰度值;A为条纹图背景值;B为调制强度函数;φ(x，y)为待求相位场.δi为第i幅图的相移值.令相移分别为，由式(1)得

对式(2)求反正切，即可得相位值φ.

2 相位补偿测量原理

实际的相移会和理想的相移有一些微小的差异，即不可避免地会存在相移误差，而这种相移误差将导致相位计算的误差.

设实际的相移为

式中，δi为第i次相移的名义相移量;Δδi为第i次相移的相移误差，则4幅条纹图的光强分布为

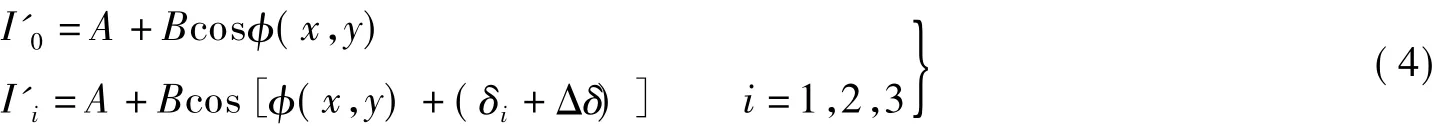
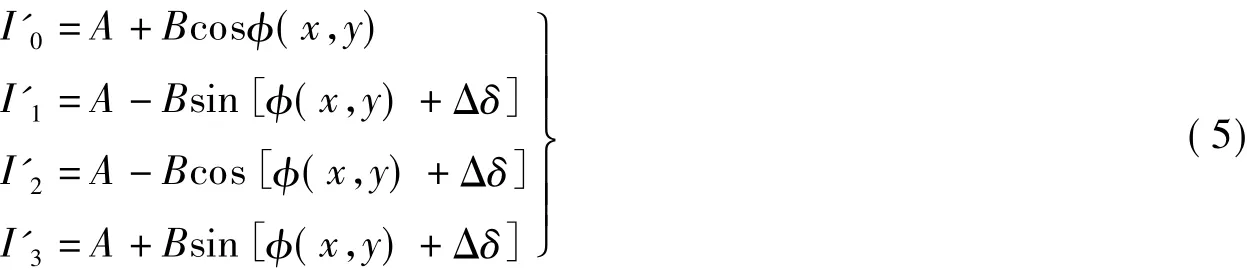
则

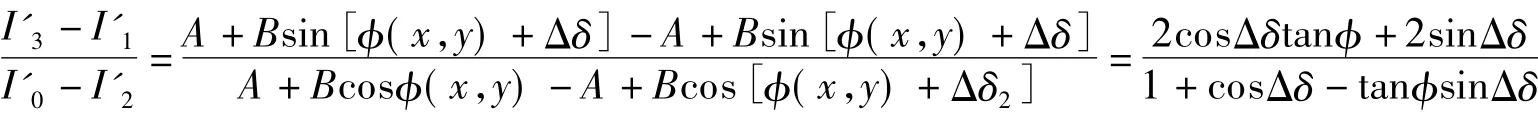
式中，Δδ一般比较小，可利用近似计算公式sinΔδ≈Δδ，cosΔδ≈1则得到四步相移算法的相位补偿计算公式［12－13］:

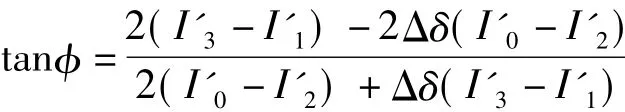
反正切后得

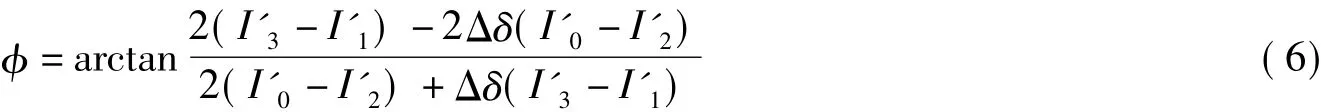
3 相位提取过程中相移误差分析

在PMP中，在一切理想的情况下，只需步进二次得到三幅条纹图，就可以得到物体的被测位相，但是在实际中，由于总是存在电噪声，探测器的非线性，以及步进的相移控制不准确等原因，为了抑制误差的影响，一般至少要步进3次得到4幅条纹图.相移误差对相位重构的精度影响较大，下面以四步相移法为例，对相位提取算法公式中的相移误差进行了分析.

在相移3次得到4幅条纹图的情况下，由于相邻像素点间隔距离非常小，因此可近似认为投影到平板后的正弦条纹中3个相邻像素点间相位差是相等的.在图2中取相邻像素A，B，C三点，则A，B，C三点间相位差相等.即有 φ′n－φn=φ″n－φ′n.

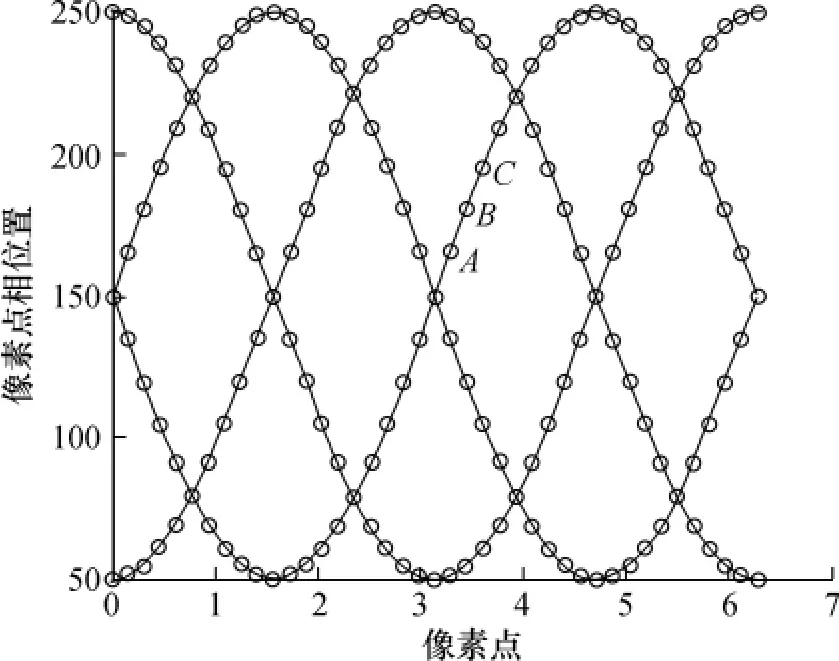
图2 正弦条纹曲线图

对图中A点有如下方程:

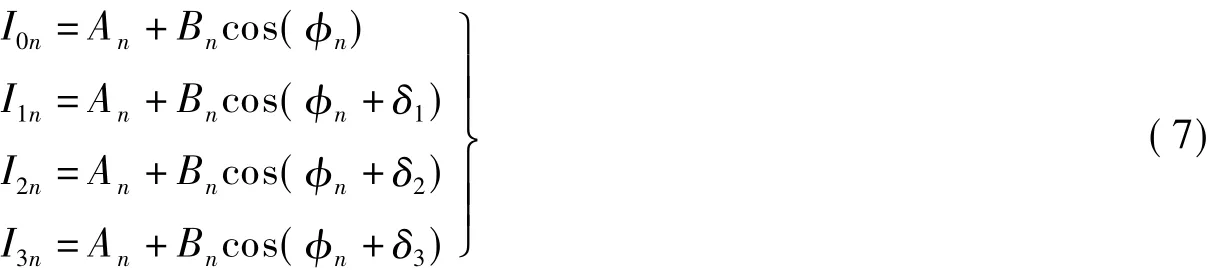
An，Bn，φn分别表示各点的背景光强，条纹的对比度和被物体高度调制的条纹位相.δ1，δ2，δ3分别表示步进3次，每步步进的相移

同理对图中B点有

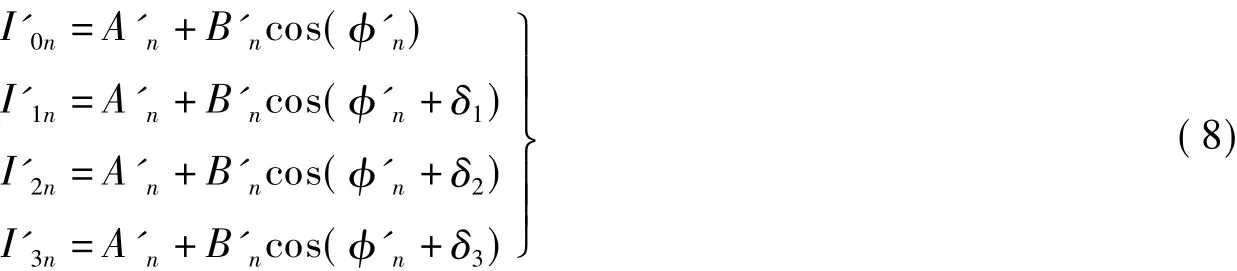
同理对图中C点有

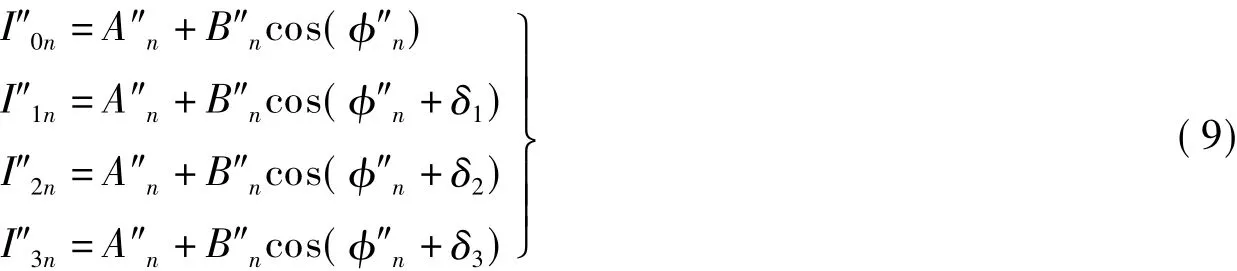
对图中A，B，C三个点有

由方程(7)可得

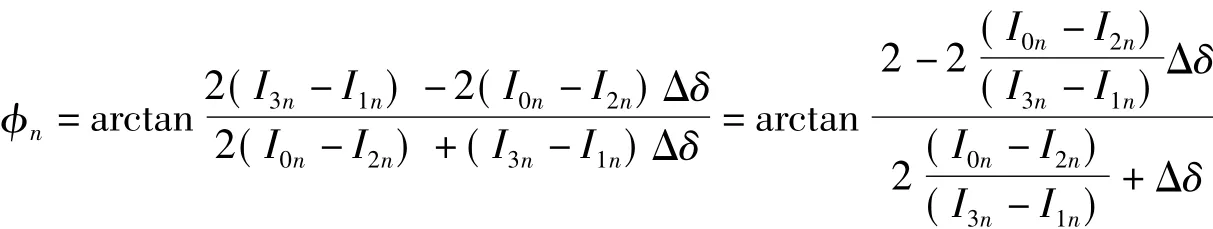
同理由式(8)可得

由式(9)可得

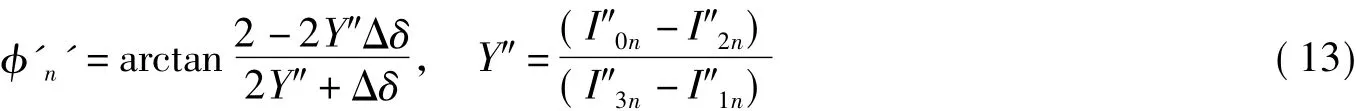
将以式(11) ～(13)代入到方程 φ′n－φn=φ″n－φ′n中得

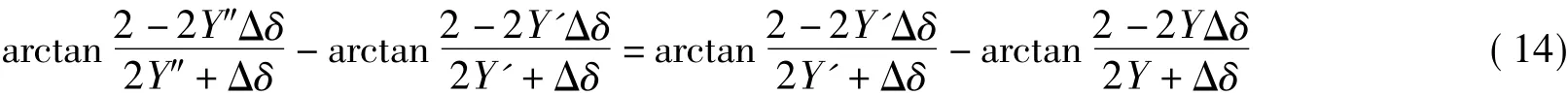
整理可得

其中，A=(Y′－ Y″)(4YY′+1) － (Y － Y′)(4Y′Y″+1);B=2(Y′+Y″)(Y － Y′) － 2(Y+Y′)(Y′－ Y″);C=6(Y′－Y″)(2YY′+1) －6(Y －Y′)(2Y′Y″+1);D=4(Y′+Y″)(Y － Y′) －4(Y+Y′)(Y′－ Y″);E=8(Y′－Y″)(YY′+1) －8(Y －Y′)(Y′Y″+1).

由上述方程即可求出较精确的相移误差Δδ.下面通过实验验证这种方法提取出的相移误差是否准确.

4 相移误差仿真计算

下面利用本文提出的提取相移误差的算法，通过仿真验证算法的有效性与精确性.

表1 仿真计算值

图3为误差补偿前后相移误差的波动仿真图，曲线2为误差补偿前相移误差波动曲线，曲线1为误差补偿后波动曲线.从图中可见，误差补偿后相移偏差基本消除.

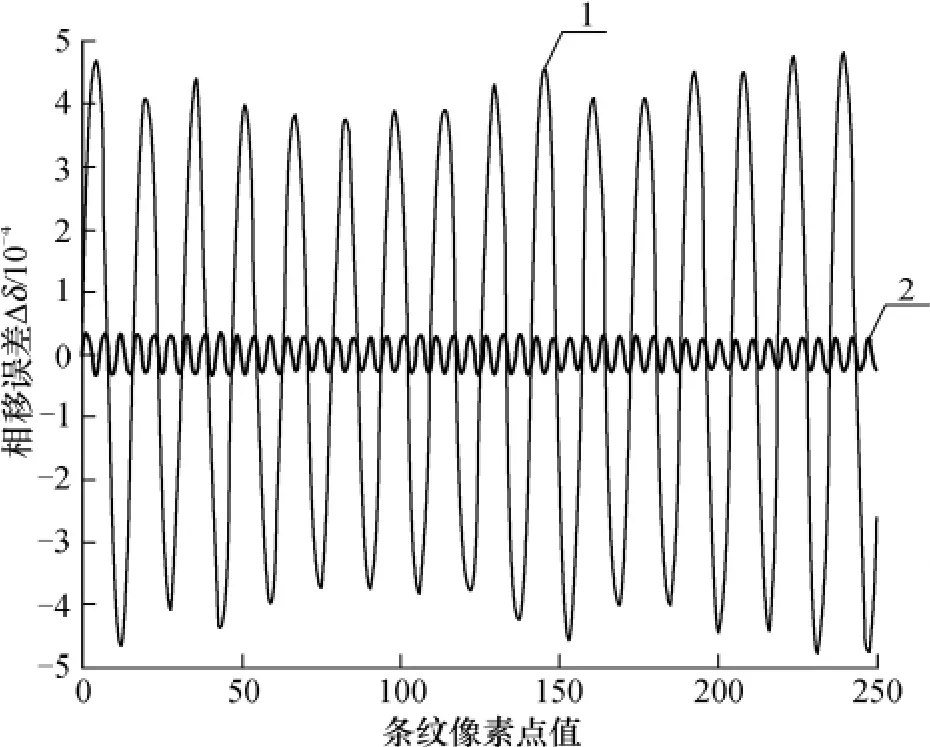
图3 误差补偿前后相移误差波动仿真图

5 实验结果

将本文提取相移误差算法运用到实际测量中，即可看出相移误差补偿后的测量效果.图4(a)、(b)分别为相移误差补偿前和补偿后恢复的三维平面图，图4(b)显然要比图4(a)平滑得多，三维重构效果较好，验证了该方法对相移误差进行补偿能有效提高物体三维测量精度.

图4 恢复的三维平面图

6 结语

由于测量精度会受到光照条件、相移误差、高度恢复算法及扫描过程中的同轴度及等间距扫描等条件的限制，所以对正弦光栅像的相移误差的准确提取并进行补偿，能有效提高测量精度.通过以上的理论分析和仿真实验，可以看出本文算法基本上能消除由相移误差引起的相位偏移，实物仿真测量效果证实了本文提出的提取相移误差的方法是正确的和有效的，对提高采用相移技术的三维测量法的精度具有一定意义.

References)

［1］ Morgan C J.Least－squares estimation in phase measurement interferometry ［J］.Opt Lett，1982，7(8):368－373.

［2］ Greivenkamp J E.Generalized data reduction for heterodyne interferometry ［J］.Opt Eng，1984，23(4):350－352.

［3］ Freischlad K，Koliopoulos C.Fourier description of digital phase－measuring interferometry［J］.J Opt Soc Am A，1992，7(4):1740－1748.

［4］ Schwider J，Burow R，Elssner K－E.Digital wavefront measuring interferometry:some systematic error sources［J］.Appl.Opt，1983，22(21):3421－3432.

［5］ Surrel Y.Design of algorithms for phase measurements by the use of phase－shifting［J］.Appl Opt，1996，35(1):51－60.

［6］ Mei H，Han－hen N，Qing－Xiang L.Algorithm in phase－stepping interferometry based on characteristic polynomial［J］.Acta Optica Sinica，2003，23(7):874－878.

［7］ Joenathan C.Phase－measuring interferometry:new methods and error analysis［J］.Appl Opt，1994，33(19):4147－4155.

［8］ Malacca－Doblado D，Dorrio B V.Family of detuning－insensitive phase－shifting algorithms［J］.J Opt Soc Am A，2000，17(10):1857－1863.

［9］ Langoju R，Patil A，Rastogi P.Predicting phase steps in phase－shifting interferometry in the presence of noise an harmonica［J］.Appl Opt，2006，45(24):6106－6112.

［10］ Estrada J C，Servin M，Quiroga J A.Easy and straightforward construction of wideband phase－shifting algorithms for interferometry［J］.Opt Lett，2009，34(4):413－415.

［11］ Servin M，Estrada J C，Quiroga J A.Spectral analysis of phase shifting algorithms［J］.Opt Express，2009，17(19):16423－16428.

［12］王吉元，田爱玲，王红军.四步相移干涉量的相位补偿及仿真［J］.西安工业学院学报，2005，25(1):23－25.Wang Jiyuan，Tian Ailing，Wang Hongjun.Phase error compensation algorithm and simulation in four step phase shifting interferometry［J］.Journal of Xi′an Technological University，2005，25(1):23－25.(in Chinese)

［13］惠梅.对相移误差不敏感的四帧相位算法［J］.清华大学学报:自然科学版，2003，43(8):1017－1019.Hui Mei.Four－frame phase－stepping interferometry－base insensitive algorithm to phase－stepping error［J］.Journal of Tsinghua University:Science and Technology，2003，43(8):1017－1019.(in Chinese)