动态闭环复杂配送网络路径优化算法研究

张 旭 凤， 张 永 安， 杨 丽

（1.北京物资学院物流学院，北京市 101149；2.北京工业大学经济与管理学院，北京市 100124；3.南京航空航天大学经济与管理学院，江苏 南京 210016）

一、引言

随着物流业的全球化、信息化与一体化发展，物流配送在整个物流系统中的作用变得越来越重要。物流配送本质上是运输，因此创造空间效用自然成为它的主要功能。但物流配送又不同于运输，它是运输在功能上的延伸。物流运输系统是物流配送系统中最重要的一个子系统，运输费用超过企业物流总消耗的40%，[1]降低物流成本首先要从降低物流配送的运输成本开始。其中，运输路径的合理性直接影响物流配送速度、成本和效益，特别是多用户物流配送路径的确定是一项复杂的系统工程。车辆路径的恰当选取，有利于加快对客户需求的响应速度，提高服务质量，增强客户对物流环节的满意度，降低服务商运作成本。

基于发展循环经济、绿色物流的理念，本文将逆向物流配送与正向物流配送相结合，并在此基础上提出闭环物流配送。所谓闭环物流配送即充分考虑传统物流配送过程中出现的逆向物流，并将正向物流配送与逆向物流配送结合起来进行系统分析和处理，使整个物流配送系统变得更加合理。因此，闭环物流配送网络不仅包括传统的正向物流配送网络，同时还包括退货和废旧品回收再利用的逆向物流配送网络，而且最为重要的是两条配送网络上的物流并非相互独立，而是呈现出“从源到汇，再由汇到源”的闭环特征。因此，从物流角度讲，闭环物流配送实质上是通过产品的正向交付与逆向回收再利用，使“资源—生产—消费—废弃”的开环过程变成“资源—消费—再生资源”的闭环反馈循环过程。[2]逆向物流配送网络是闭环物流配送网络上的一个特殊环节。然而，闭环物流配送网络不是简单地将正向物流配送网络与逆向物流配送网络相加，而是涉及从战略层到运作层的每一个层面，比传统物流配送要复杂得多。它不仅具有传统物流配送所有的特点，而且增加了许多新的特性。闭环物流配送的存在不仅是环境与可持续发展的要求，而且也是企业自身发展和获取竞争优势的需要。环境与非环境因素共同造就了闭环物流配送的产生和发展。

闭环物流配送网络是配送过程中相互联系的组织与设施的集合，是由物流配送节点与运输线路连接而成的一个网络，根据逆向物流方式的不同，可分为制造商自己负责逆向物流配送、委托零售商负责逆向物流配送和委托第三方负责逆向物流配送三种。本文重点研究制造商自己负责逆向物流配送的闭环物流配送网络，如图1所示。网络中的运输线路代表不同库存或储存点之间货物的移动路线，而物流配送节点就是商品的储存点或需求点，如仓库、配送中心、物流中心、工厂、供货商或零售店等。任意一对物流节点之间都可能有多条运输线路相连接，这些线路代表了不同的运输方式、不同的运输路线或不同的商品。物流节点也代表那些货物流动过程中的临时经停点，如货物在运达零售店或最终消费者之前进行短暂停留的仓库。

图1 制造商自己负责逆向物流的闭环物流配送网络

二、相关研究综述

对于物流的复杂性特点，学者们从不同角度出发进行了研究。张贝[3]对逆向物流网络设计的复杂性进行了研究，并对逆向物流网络设计模型与方法进行了分析与总结。王玉琳等[4]对物流管理系统组成的多元化和复杂性、功能的整体性、运作机制的随机动态性和开放性等特征进行了分析。张公让等[5]认为，物流管理具有结构、环境、行为等方面的动态、开放、凸显等特点，属于复杂系统的范畴。赵国智等[6]分析了煤炭物流网络的复杂网络特征，并运用复杂网络的相关理论与方法分析煤炭物流网络，对基于复杂网络的煤炭物流网络优化方法进行了研究。

对于车辆路径优化问题，学者们从不同方面利用不同方法进行了大量研究，主要可分为精确算法和近似算法两大类。求解车辆路径优化的精确算法主要包括分支定界算法、[7]列生成算法、[8]动态规划算法、[9]分支切割算法；[10]求解车辆路径优化的近似算法包括人工神经网络算法、遗传算法、模拟退火算法、禁忌算法等。

目前，有关逆向物流定量模型的研究大多集中于网络结构。1989年，梅恩（Min）首先提出了同时收发送的混合车辆路径优化问题（简称VRPSDP）。[11]2001年，戴德罗夫（Dethloff）又重新提出该问题。[12]车辆路线问题还包括一类有回载的车辆路线问题（简称VRPB），[13]主要考虑收集和配送为各自独立的两个部分的情形，车辆从某些客户点收集产品后再配送到另外的某些客户点，没有考虑正向物流与逆向物流的整合。戴德罗夫指出，VRPB的求解方法不能用于解决VRPSDP问题。[14]上述文献本质上属于车辆路线优化问题，其目标是行驶路线最短，但多数研究并没有考虑逆向物流的复杂性特点以及逆向物流与正向物流的有机整合。

针对上述逆向物流与正向物流整合中的物流配送路径优化问题，本文采用一类动态规划模型来对闭环复杂物流配送网络路径优化问题进行研究。

三、物流配送网络的复杂性分析

物流配送网络具有时空复杂性的重要特点，是一个与我们的生活、工作、社会经济环境密切相关的复杂大系统。应用复杂网络理论从理论上分析物流配送网络拓扑结构复杂性，是研究复杂物流配送网络的关键所在，也是物流配送网络研究的基础理论问题之一。物流配送系统的运行效率受多方面因素的影响，要从整体、宏观的角度去了解物流配送网络，就要对系统各个部分之间的相互作用有一个清晰的认识。物流配送网络不仅具有与其他复杂网络相似的一些拓扑特性，而且具有不同于其他复杂网络的显著特点，比如自主性和选择性。而通过融合物流配送网络自身的特点，深入分析拓扑结构对物流配送网络承载力的影响以及缓解物流瓶颈问题的策略是物流配送网络复杂性研究中非常重要的方面。同时，还必须从系统的角度出发，对物流节点以及节点的物流特征进行分析与合理的规划和管理，以达到有效缓解物流配送瓶颈的目的。此外，对本身是动态实体的物流配送网络来说，适应性和动态性也是其基本特性。这意味着物流配送网络拓扑结构不是固定的、成熟的，也不是一成不变的。相反，由于外部作用的驱动或者内部元素的作用，允许它随时间进行演化和调节。因此，有关这方面的研究可以从宏观角度帮助我们理解物流配送网络演化的内在机理和运行规律，进而为提出解决物流问题的有效方法提供理论依据，为切实提高整个物流配送网络承载能力，充分利用现有交通资源降低我国物流配送网络建设设计、管理和控制的盲目性，科学制定我国物流发展战略规划，发展先进的物流管理与控制技术打下坚实的理论基础。

物流配送网络是一个复杂的网络结合体，单就物流配送网络所要实现的某一特定功能而言，可以比较容易地将其归类于某一种网络。比如，仅考察物流配送工具（如车辆）在物流配送网络上的活动，可将之归类于社会网络；而仅考察物流配送网络承担的物流量的分配，可将之归类于技术的分配网络；仅考察物理层面的物流配送网络，其物流配送网络的形成可归类于技术网络的构建。而物流配送网络恰恰是这些功能的承载体，是混合型的复杂网络。

此外，对于物流配送网络拓扑结构的复杂性完全可以用复杂网络的理论进行研究，主要包括三个方面：（1）就简单的拓扑统计规律而言，物流配送网络的整体集合可能具有规则网络的某些特性，但根据我们研究的对象及目的，完全可以根据不同的拓扑表示方式对其进行抽象，从而展示出非常复杂的重要拓扑特征。（2）就其动力学行为或特征而言，它具有明显的复杂性特征。如物流节点不停地进行物流库存产生和转移，这些节点之间已经不再是简单的起点与终点的关系。另外，物流配送网络节点上物流阻塞的形成、传播及消散等规律也具有非常复杂的动态特性。因此，它在简单的貌似规则网络的平面格子上不得不背负着复杂网络相关统计动力学特性，如物流流量的分配、阻塞的传播与消散等。（3）就物流配送网络的演化特征而言，网络拓扑对物流配送网络上物流流量分布及其他动力学过程具有潜在的巨大影响。

复杂网络上的物流配送动力学研究所依赖的底层拓扑基于两个基本思想：（1）通过一般的网络产生机制给定一个底层的拓扑，在这样的拓扑上进行各种动力学演化；（2）网络上的动力学行为反过来影响网络拓扑演化。

目前，复杂网络在物流配送网络系统中所对应的是物流配送网络系统的拓扑结构、物流配送网络系统的形成和演化以及物流配送网络系统的动力学机制和稳定性等问题。

四、任务模型与系统模型

由于闭环物流配送系统中双向的物流配送增加了闭环物流配送网络规划的困难，因此设施的有效共用能有效降低物流成本，也就是说，物流配送网络中制造商、配送中心及零售商等的设施也可以进行废旧品处理或缺陷品回收等。最终客户在地域上的分散性以及拥有废旧品的少量性，使得正向物流和逆向物流配送线路与运输能力的整合，常常导致高昂的废旧品回收成本。由于回收与配送差异巨大，合理安排产品与废旧品之间的运输线路与运输能力变得至关重要。因此，本文考虑由制造商退还货物和废旧品。

闭环物流配送系统涉及物流配送节点的地理位置、交通运输条件、配送物资的供求关系以及回收物资等客观因素，我们可根据这些将物流配送网络划分为若干物流配送子系统。

我们将之划分为 n 个子系统，t=1，2，…，n。

假定在一个时间周期内，从系统内的一个物流配送中心（假定为节点1）发出一辆物流配送车向该系统内的各个节点配送物资，配送完成后再把各个节点的物资（包括退货与回收物资）送回节点1。试研究物流配送车行驶的最短路径及行驶路线。

五、算法设计

依据问题的特点，建立闭环物流配送路径优化动态规划模型如下：

根据问题的要求，从节点1出发到最后回到节点1，中间需要经过n个节点，将子系统物流配送问题划分为n个阶段，阶段变量 k=1，2，…，n。

假定物流配送车从节点1出发行驶到节点i，记Ni={2，3，…，i-1，i+1，…，n}，用以表示由节点 1 到节点 i可能经过的中间节点的集合，Q表示由节点1到节点i经过的中间节点的集合，则Q∈Ni。

状态变量用（i，Q）表示，即物流配送车从节点1出发行驶到节点i，中间所经过节点的集合为Q。（i，θ）表示物流配送车从节点1出发，直接行驶到节点i，中间不经过其他节点，其中θ表示空集。

决策变量pk（ik+1，Qk）=ik表示决定配送车从节点ik-1行驶到节点ik。

最优值函数fk（i，Q）表示配送车从节点1经过k个中间节点（Q表示k个中间节点的集合）到达节点i的最短路线距离。

建立递推公式如下：

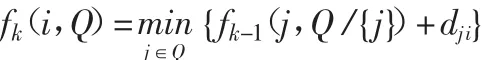
其中，k=1，2，…，n-1；i=2，3，…，n。

其中，边界条件f0（i，θ）表示配送车从节点1出发不经过中间节点（Q=θ）直接到达节点i的距离dji。

最优值函数fn-1（1，Nn，1），Nn，1={2，3，…，n}，即为所求第n个子系统的配送车从节点1出发到达其他n-1个中间节点一次且仅一次，再回到节点1的最短路线距离。配送车行配送车从节点1出发经过k个中间节点一次且仅一次（Qk的前一个节点ik。

在每个子配送系统优化的基础上，可最终实现整个物流配送网络系统路径的最优化：

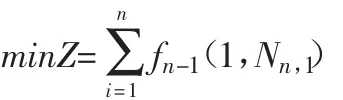
其中，Z表示n个子配送系统中物流配送车行驶距离的总和。

六、算法应用

某闭环复杂物流配送网络如图2所示。其中，某子物流配送网络中的配送中心A下属五个商品超市，配送中心A每天从配送中心发出配送车，将商品配送到每个超市，卸货后再将退货和回收品装车，依次到达下一个目的地，最后将退货和回收品带回配送中心。表1给出了配送中心与五个超市之间的距离（单位：公里），要求配送车从配送中心出发经过每个超市一次且仅一次，最后回到配送中心，求配送车行驶的最优路线与最短距离。

我们把配送中心、超市1、…、超市5依次进行编号，分别设为节点 1、节点 2、…、节点 6。由题设条件 dij≠dji，i≠j，i，j=1，2，…，6可知，此配送系统的交通图是一个有向多重连通图。根据上述讨论，我们采用顺推法求解物流配送车行驶的最优路线和最短距离。

最后得到物流配送车最优行驶路线为节点1→节点2→节点6→节点5→节点4→节点3→节点1，最短距离为114公里。

七、结论与展望

图2 某物流配送网络图

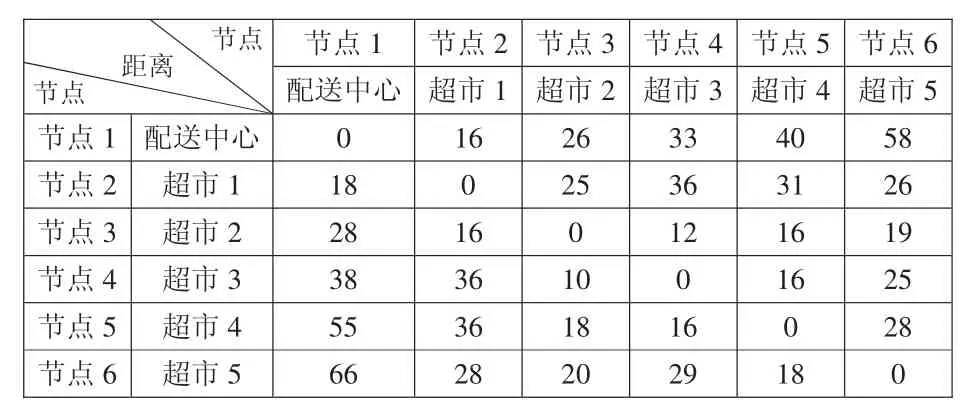
表1 各节点物流配送距离

1.研究结论。本文通过对物流配送网络复杂性的分析，利用动态规划算法对目前闭环复杂物流配送网络中的最优路径精确计算问题进行了研究。经验证，计算结果与实际情况相符合。本文虽然只对闭环复杂物流网络中某一子系统的物流配送路径优化进行了研究，但对于整个闭环复杂物流配送网络来说，可利用这种方法，将各子系统中的物流配送中心作为配送目标节点，将物流网络中总的配送中心作为配送中心，依此类推，从而能够对整个物流配送网络以及某个子物流配送网络的配送路径进行优化研究。

使用本文方法，可将子物流配送网络的路径优化研究扩展到整个复杂物流配送网络的路径优化研究，为研究整体闭环复杂物流配送网络路径优化问题提供新的思路。

2.研究的局限性。本文仅对具有6个节点的子物流配送系统进行了计算，最优解的求解较为容易。如果子系统节点很多，手工计算的工作量很大，就需要借助计算机及相应软件来进行计算。另外，本文只对退货及回收物资与所送物品可同用一车载送的问题进行了分析，而未考虑正向物流物品与逆向物流物品不可同载的问题。

在以后更进一步的研究中，需要在考虑上述问题的同时，继续研究制造商处理回收品时如何解决某些客户具有的优先权问题以及回收品数量为随机变量情况下的闭环物流回载策略问题等。

[1]刘志强，丁鹏，盛华烨.物流配送系统设计[M].北京：清华大学出版社，2004：22-37.

[2]冯之浚，张伟，郭强等.循环经济与末端治理的范式比较研究[N].光明日报，2003-09-22（3）.

[3]张贝.逆向物流网络设计复杂性分析及研究现状[J].物流技术，2005（12）：41-43.

[4]王玉琳，王诤诤.现代物流管理系统的复杂性分析[J].系统辩证学学报，2003，11（4）：88-91.

[5]张公让，代军旗，杨波.物流管理系统中的复杂性特征研究[J].价值工程，2009（4）：70-73.

[6]赵国智，王喜富等.煤炭物流网络的复杂性分析及优化方法研究[J].物流技术，2008，27（8）：117-119.

[7]N.Christofides，A.Mingozzi，P.Toth.Exact Algorithms for the Vehicle Routing Problem,Based on Spanning Tree and Shortest Path Relaxations[J].Mathematical Programming，1981（20）：255-282.

[8]M.Balinski，R.Quandt.On an Integer Program for a Delivery Problem[J].Operations Research，1964（12）：300-304.

[9]S.Eilon，C.D.T.Watson-Gandy，N.Christofides.Distribution Management：Mathematical Modeling and Practical Analysis[M].London：Griffin，1971：79-86.

[10]A.Letchford，R.Eglese，J.Lysgaard.Multistars，Partial Multistars and the Capacitated Vehicle Routing Problem[J].Mathematical Programming，2002（94）：21-40.

[11]H.Min.The Multiple Vehicle Routing Problem with Simultaneous Delivery and Pickup Points[J].Transportation Research Part A，1989，23A（3）：377-386.

[12]、[14]Jan Dethloff.Vehicle Routing and Reverse Logistics：the Vehicle Routing Problem with Simultaneous Delivery and Pick-up[J].Operations Research Spektrum，2001，23（1）：79-96.

[13]J.Dethloff.Relation between Vehicle Routing Problems"An Insertion Heuristic for the Vehicle Routing Problem with Simultaneous Delivery and Pick-up Applied to the Vehicle Routing Problem with Backhauls[J].Journal of the Operational Research Society，2002，53（1）：115-118.