权重信息未知的区间直觉模糊多属性决策方法

李光博,黄德才,2

(1.浙江工业大学理学院,浙江 杭州 310032;2.浙江工业大学信息工程学院,浙江杭州 310032)

权重信息未知的区间直觉模糊多属性决策方法

李光博1,黄德才1,2

(1.浙江工业大学理学院,浙江 杭州 310032;2.浙江工业大学信息工程学院,浙江杭州 310032)

针对权重信息完全未知且属性值为区间直觉模糊数的多属性决策问题,提出了一种基于线性规划和投影模型的决策方法.该方法首先引入区间直觉模糊数相离度的概念,然后,给出了一种基于加权属性值离差最大化的线性规划模型,通过求解此模型得到相应的属性权重.进而利用各个方案的加权属性值在加权模糊正理想点上的投影对方案进行排序.最后用实例说明了该方法的可行性和有效性.

区间直觉模糊数;多属性决策;属性权重;相离度

自Zadeh[1]建立了模糊集理论,数学的理论与应用研究范围便从精确问题拓展到了模糊现象的领域.并在模式识别、决策分析等诸多领域得到了广泛的应用.但随着社会问题的日益复杂化以及科学研究的不断深入,传统的模糊集理论因其不能完整地表达所研究问题的全部信息而在实际应用中受到越来越多的制约和挑战.故 1986年保加利亚学者A tanassov[2-3]拓展了传统的模糊集,提出了直觉模糊集的概念.由于直觉模糊集同时考虑了隶属度、非隶属度和犹豫度三方面的信息.因此,它能够更加细腻的描述和刻画客观世界的模糊性本质,使得在处理不确定信息时具有更强的表现能力,更具灵活性,故直觉模糊集引起了学术界的关注.A tanassov[4]等进一步拓展了直觉模糊集,提出了区间直觉模糊集的概念.文献[5]定义了区间直觉模糊集的一些基本运算法则.文献[6-7]则把传统的理想点决策法拓展到区间直觉模糊集决策领域.文献[8]对区间直觉模糊信息的集成方法进行了研究,提出了区间直觉模糊数算术平均(IIAA)算子、区间直觉模糊数加权算术平均(IIWAA)算子、区间直觉模糊数几何平均(IIGA)算子和区间直觉模糊数加权几何平均(IIWGA)算子,并将其应用于决策中.文献[9]利用每个方案的得分向量和区间直觉模糊理想点之间的余弦函数等建立了两种投影模型来分别度量每个方案和区间直觉模糊理想点之间的相似度,并以此给出排序.笔者则对权重完全未知,且属性值为区间直觉模糊数的情况进行了研究.给出了一种基于离差概念的客观赋权方法,并进一步进行决策.

1 预备知识

定义1[2]设X是一个非空集合,则称A={＜x,μA(x),μA(x)＞|x ∈ X}为直觉模糊集,其中,μA(x)和μA(x)分别表示为X中元素x属于X的隶属度μA：X→[0,1]和非隶属度vA：X→[0,1],且满足条件 0≤μA(x)+vA(x)≤1,∀x∈X.πA(x)=1-μA(x)-vA(x)表示为x中元素属于X的犹豫度.

由于客观事物的复杂性和不确定性,隶属度和非隶属度有时难以用确定的实数来表示,而用区间数表示比较合适.因此,A tanassov对直觉模糊集进行了拓展,提出了区间直觉模糊集的概念.

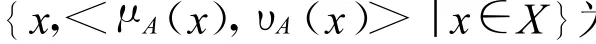
X中元素x属于X的隶属度区间μA(x)和非隶属度区间υA(x)所组成的有序区间对＜μA(x),υA(x)＞称为区间直觉模糊数,并把区间直觉模糊数一般形式记为([a,b],[c,d]),其中[a,b]⊂[0,1]⊂[c,d]⊂[0,1],b+d≤1.

定义3 设γ1=([a1,b1],[c1,d1])和γ2=([a2,b2],[c2,d2])为任意两个区间直觉模糊数,则称：为区间直觉模糊数γ1和γ2之间的相离度.

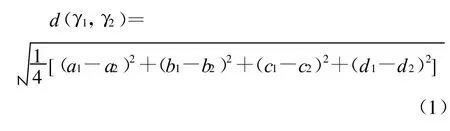
易证 d(γ1,γ2)具有如下性质：

定理 1 设γ1,γ2,γ3为任意三个区间直觉模糊数,则

(1)0≤d(γ1,γ2)≤1,特别地,d(γ1,γ1)=0.

(2)d(γ1,γ2)=d(γ2,γ1).

(3)d(γ1,γ2)≤d(γ1,γ3)+d(γ2,γ3).

2 决策原理与方法

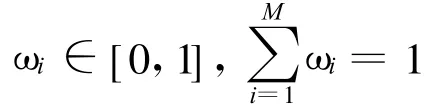
由于属性权重未知,而属性权重的不确定性会引起决策方案排序的不确定性.一般地,若所有决策方案在属性下的属性值差异越小,则说明该属性权重对方案决策的作用越小;反之,若属性能使所有决策方案的属性值有较大的差异,则说明该属性对方案决策将起重要作用.因此,从对决策方案进行排序或择优的角度考虑,无论方案属性值本身重要程度如何,方案属性值离差越大应该赋予越大的权重,离差越小就应该赋予越小的权重.特别地,若所有决策方案在属性下的属性值无差异,则此属性对方案的决策将不起作用,可令其权重为零[10].

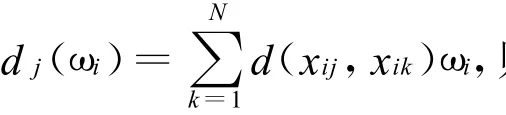
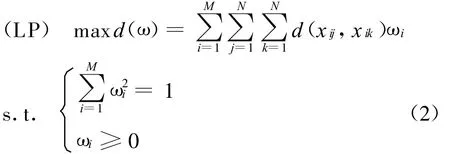
解此模型,构造Lagrange乘子函数：

显然式(3)就是式(2)的最优解,详细证明过程请参阅文献[10].

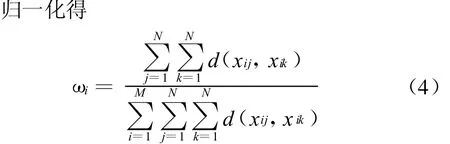
由上可得属性权重向量集 ω=(ω1,ω2,…,ωM)T,至此,我们可以用已有的方法进行排序或择优.根据以上分析,给出如下具体决策步骤：

步骤1 根据所给信息,建立区间直觉模糊决策矩阵A=(aij)M×N.

步骤2 如权重向量完全未知,则求解线性规划式(2),得到最优权重集ω.

步骤3 求得权重向量积 ω后,可按照不同的参照基准进行择优或排序.如理想点法,投影模型法等.

3 实例分析

假设某军方欲采购火炮装配部队,主要考虑五项指标(属性)：(1)火力突击能力(C1);(2)反应能力(C2);(3)机动能力(C3);(4)环境适应能力(C4);(5)成本(C5).现有4种系列火炮Ai(i=1-4)(方案)可供采购,每种系统在各属性下的评估信息经过统计和处理后,可表示为区间直觉模糊数.如表1所示,采购部门应如何采购火炮.

表1 决策矩阵Table1 Decisionmatrix

为了确定最优方案,下面利用笔者方法给出具体决策步骤.

步骤 1 建立区间直觉模糊决策矩阵为A=(aij)5×4.

步骤2 因为属性权重信息未知,由式(1-4)建立线性规划模型求得最优权重向量：

ω=(0.20,0.21,0.19,0.18,0.22)T步骤3 当属性值和属性权重向量都已知,我们可以用已有的决策方法进行决策,如用文献[9]中的投影模型法,首先求各个方案的加权得分向量和区间直觉模糊理想点A+的加权得分向量如下：

然后利用投影公式确定每个方案在理想点A+上的投影

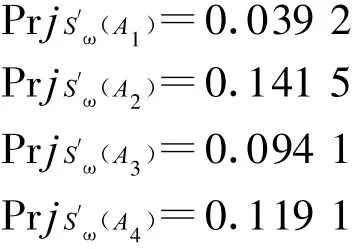
最后按照 Pr j′ω(Ai)的值的大小对方案 Ai进行排序：

所以最理想的方案是 A2,既第二个配系方案最佳.

4 结 论

针对属性权重完全未知,且属性值为区间直觉模糊数的不确定型多属性决策问题,给出了一种基于线性规划和模糊投影的决策方法,该方法基于加权属性值离差最大化建立一个线性规划模型获得了相应的属性权重.进而用模糊投影法进行排序或择优.通过实例分析,证明了该方法的有效性和实用性,因而该方法在属性权重完全未知的区间直觉模糊多属性决策中值得推广.

[1]ZADEH L A.Fuzzy sets[J].Information and Control,1965,8(3)：338-356.

[2]ATANASSOV K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1)：87-96.

[3]ATANASSOV K.More on intuitionistic fuzzy sets[J].Fuzzy Setsand Systems,1989,33(1)：37-46.

[4]ATANASSOV K,GARGOV G.in terval-valued intuitionistic fuzzy sets[J].Fuzzy Sets and Sy stem s,1989,31(3)：343-349.

[5]ATANASSOV K.Operatorsover in terval-valued intuitionistic fuzzy sets[J].Fuzzy Sets and Sy stem s,1994,64(2)：159-174.

[6]胡辉,徐泽水.基于TOPSIS的区间直觉模糊多属性决策法[J].模糊系统与数学,2007,21(5)：108-112.

[7]卫贵武.一种区间直觉模糊数多属性的TOPSIS方法[J].统计与决策,2008,253(1)：149-150.

[8]徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].控制与决策,2007,22(2)：215-219.

[9]徐泽水.直觉模糊信息集成理论及应用[M].北京：科学出版社,2008：179-183.

[10]WANG Ying-m ing.On fuzzy multiattribute decision-making models and m ethods with incom plete p reference information[J].Fuzzy Sets and System s,2005,151(2)：285-301.

A decisionmakingmethod of interval-valued intuitionistic fuzzymultip le attributesw ith unknown attributeweight information

LIGuang-bo1,HUANG De-cai1,2
(1.College of Science,Zhejiang University of Technology,H angzhou 310032,China;2.College of Information Engineering,Zhejiang University of Technology,H angzhou 310032,China)

with regard to decision m aking p rob lem of the interval-valued intuitionistic fuzzy multip le attributesw ith com plete unknown attributeweights,a decision making method based on the linear p rogramming and p rojection model is proposed in this paper.Firstly,the concep t of deviation degree between two interval-valued intuitionistic fuzzy numbers is introduced.Then,a linear programming model based on the maximizing deviation of weighted attribute values is presented.The attribute weights are obtained through solving the m odel.Furtherm ore,the programs are ranked by using the projectionsof theweighted attribute values in each program on the weighted fuzzy positive ideal point.Finally,a case study is given and the result show s this method is feasib le and effective.

inter-valued intuitionistic fuzzy numbers;multiple attributes decision making;attribute values;deviation degree

O159

A

1006-4303(2010)04-0411-04

2009-02-27

浙江省自然科学基金资助项目(Y107596)

李光博(1982—),男,陕西定边人,硕士研究生,研究方向为模糊决策.通讯联系人：黄德才教授,E-mail：hdc@zjut.edu.cn.

(

陈石平)