互通式立交匝道与主线开口处设计浅析

张 颖 郭立臣

1 概述

互通式立交的匝道与主线开口处是指立交匝道与主线的分岔端,也称楔形端。楔形端的设计是互通立交设计的一个极重要的关键点,楔形端的设计直接关系到行车的安全性与舒适性。目前,对楔形端的设计有多种不同的方法,本文主要对比较常用的四种方法进行分析,四种方法适用情况不同,各有利弊。

2 匝道与主线连接处断面设计方法

2.1 第一种方法

楔形端断面设计的第一种方法是匝道的横坡取值与主线横坡相同,纵坡取值采用分流点或合流点对应主线桩号切线纵坡,不考虑出入口角及路面横坡的影响,近似地用楔形端处主线纵坡值作为匝道的起始纵坡。这样可使问题简单化,再加上设计者对简化后纵坡变化的判断,就能使匝道纵面得到控制,并不致在详细设计时纵坡出入过大。这种方法计算简单、复核方便,但误差稍大,一般用于初步设计阶段。

2.2 第二种方法

第二种方法是设路面为一个平面,通过主线割线纵坡和横坡及分流鼻前5 m～10 m匝道上一点的驶出、驶入角度α来确定匝道的纵坡、横坡。

取分合流鼻点处匝道桩号对应的主线设计中心线 A,及 A点前5 m～10 m处一点B,如图1所示。

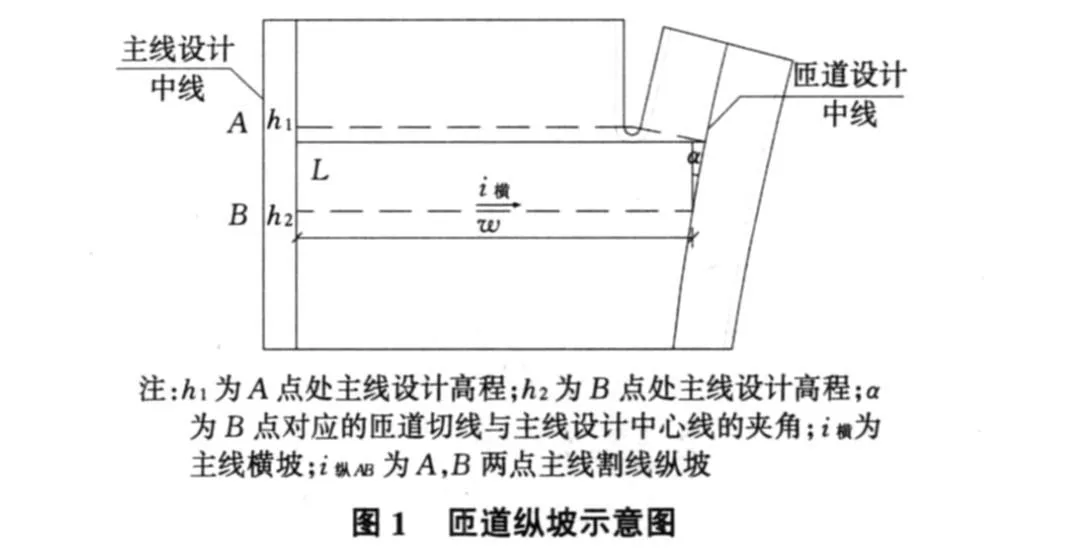
对匝道纵坡进行计算,则匝道纵坡为:

取分、合流点对应的主线中线点为 C,取从分、合流点对应的匝道中线点引出垂直于主线中线点为D,如图2所示。

对匝道横坡进行计算,则匝道横坡为:

第二种方法中,B点的取值较有随意性。不同的设计人所取B点不会相同,但其误差均在可允许的范围内。

2.3 第三种方法

第三种方法为楔形端分合流鼻点处的微分取值法。

这种方法是用主线纵坡、路面横坡及出入口角度来求相接处的匝道纵坡,公式推导如下:

设相接处断面为AP,该处的主线纵坡为 IM,路面横坡为IC,求匝道纵坡 IS。

在AP断面处,取一主线长为ΔX的微分体,其匝道长度为ΔL,断面宽度增量为ΔY,平面图如图3a)所示。而这里高程所研究的范围在 AA′B′C内,设 A,A′,B′,B,C各点的设计高程分别为HA,HA′,HB′,HB,HC,其相应的高程立面如图3b)所示。

则 IS=(HC-HA)/ΔL,而 ΔL=ΔX/cosθ HC=HB-ICΔY 。

则 IS=[(HB-HA)/ΔX]-ICΔY/ΔXcosθ。

当ΔX→0时,有:

则有:

当主线路中至外侧的路面横坡IC为正坡时(外高中低),式(3)则为:

第三种方法匝道横坡计算与第二种方法一致。

2.4 第四种方法

第四种方法为脊线法。在主线外侧行车道边线与匝道内侧行车道边线交点至分合流鼻点之间设置一条合理的脊线,匝道的纵断面和横断面设计自匝道起点开始便不依附主线。匝道起点的纵坡为该点相对应的主线切线纵坡。匝道横坡则根据自身需要设定,这种做法施工中路面会存在一条脊线,影响路面整体平整度,但是匝道的线形却更适合行车。

3 楔形端纵横坡取值实例计算

图4为天津市塘沽区西中环北延京津互通式立交,D匝道与西中环北延主线分流点。

采取第一种方法时,匝道横坡 i横=1.5%;匝道纵坡 i纵=-1.46%;

采用第二种方法时,主线横坡i横=1.5%;A,B两点主线割线纵坡 i纵AB=-1.391%;C,D 两点主线割线纵坡 i纵CD=-1.447%。

代入式(1),可得匝道纵坡 i纵为:

代入式(2),可得匝道横坡 i横为:

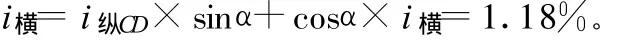
按第三种方法取值匝道横坡IC与第二种方法一样,匝道纵坡IS计算方法为:主线横坡 IC=1.5%;主线纵坡IM=-1.46%。其中,θ=11.56°,代入式(3):

按第四种方法设置脊线匝道横坡 i横=3%;匝道纵坡 i纵=0.73%。

4 结语

1)本文对互通式立交楔形端设计的4种方法进行了理论推导和实例分析,从本文分析可以看出,第一种方法纵横坡的取值比较简单,适合于初步设计阶段,精确性不如其他三种方法,一般不能用于施工图设计。

2)第二种和第三种方法是目前设计中经常使用的设计方法,作者建议在有条件的情况下,应采用本文所述第三种方法进行楔形端纵横坡设计。

3)第四种方法借鉴了反坡的脊线设计法,这种方法设计的匝道行车的舒适性大大增强。鉴于匝道行车速度比较低,纵横坡变化的不连续不会对司乘人造成不适,目前的楔形端设计一般情况下没有考虑脊线设计,视觉的不平整性也使得这种方法并没有得到大规模的应用。

[1] 朱宗余.对互通式立交设计几个问题的探讨[J].中外公路,2004(15):30-31.

[2] 胡建荣,许 刚,姚国宏.互通式立体交叉匝道纵面设计问题探讨[J].交通科技,2007(1):45-46.

[3] 周 鑫.公路立体交叉技术指标合理应用研究[D].上海:同济大学交通运输工程学院,2008.

[4] 钟伟斌.互通立交设计的若干问题探讨[J].中国水运,2007(1):20-21.

[5] 付胜余.关于互通式立交设计中一些问题的探讨[J].北方交通,2007(1):58-60.