乳腺癌检测的三维时域微波断层成像方法

刘广东 张业荣

(南京邮电大学电子科学与工程学院,江苏南京210003)

1.引 言

乳腺癌是国内外危害女性健康的顽疾,其危害性大,患者的死亡率高。研究表明,如果乳腺肿瘤能在早期时被及时发现并加以治疗,那么患者的五年成活率将明显提高。早期检测对降低乳腺癌患者的死亡率具有重要意义[1-2]。

比起乳腺癌常规检测方法,如X线影像技术、计算机断层摄影术、超声成像、核磁共振成像和光学成像等方法,微波成像检测技术具有辐射小、费用低、分辨率高和易普查等优点,有望成为安全实用的常规或者辅助检测手段[1-2]。

微波频段下,正常乳房组织和恶性肿瘤组织的电特性参数差异明显,它们的介电常数和电导率差异均在5倍以上,这为微波成像检测乳腺癌提供了物理基础[1-2]。

目前,微波成像方法主要有有源微波成像、无源微波成像和微波热致超声成像三种,且主要工作集中在有源微波成像。其中有源微波成像主要有微波断层成像(microwave tomography imaging,MTI)和共焦微波成像(confocal microwave imaging,CMI)两种方式[1-2]。

共焦微波成像方法借鉴了军事领域中脉冲探地雷达技术,由发射天线发射超宽带脉冲,多个接收天线接收散射信号,基于目标的电磁参数与周围环境的电磁参数的明显不同,区分出强散射区域,从而判断目标的位置[1-2]。

微波断层成像方法是一种电磁逆散射方法,通过在散射体外部观测到的电磁场来反演成像区域的电磁特征参数分布,从而判断散射体目标的位置、形状和尺寸分布等信息。所以它比共焦微波成像方法有更清晰的物理解释[1-2]。

然而,电磁逆散射属于不适定问题,是一个富有挑战性的工作[3],非线性和病态性是其中两个主要困难[3-11]。从处理非线性的方式来看,早期的线性化近似方法仅适用于弱散射体。对于高对比度反演问题,近年来主流方法是将重建问题转化为最优化问题迭代求解[3-4,10],其中,解决最优化问题的方法主要有局部寻优和全局寻优两大类[12]。无论是哪一类方法,一般都需要采用正则化方案来处理病态性[3-4,10]。

早期的电磁场数值计算多采用频域方法,它对窄带信号而言可行、经济。为了检测早期的小尺寸肿瘤病灶,需要提高重建的分辨率,因此要求利用宽带高频脉冲信号作为激励源。此时,时域方法显示了更大的优势。时域电磁逆散射是利用目标的瞬态响应波形重建目标的物理特征。相比频域方法,时域方法由于包含了更多的信息,可能获得更准确的重建结果[4,10-11]。

得益于时域有限差分(finite-difference timedomain,FDTD)法[13]和计算机水平的快速发展,近十年来已经成功建立了好几种时域电磁逆散射算法,这其中主要有Takenaka等提出的正反演时间步进(forward-backward time-stepping,FBTS)算法[4]和Rekanos等提出的拉格朗日乘子算法[7]以及Winters等人提出的时域逆散射 (time-domain inverse scattering,TDIS)算法[10-11]。其中FBTS算法在二维乳腺癌检测[4,14]、TDIS算法在二维和三维乳腺癌检测[10-11]中均已获得了重要进展[10-11],而拉格朗日乘子算法在这方面的应用还未见报道。

我们首先建立三维半球乳房模型;接着以Rekanos等人的拉格朗日乘子算法[7]为基础,应用泛函分析和变分法,导出闭式的拉格朗日(Lagrange)函数关于乳房内各介质电参数的Fréchet导数;其次,考察了噪声的影响,并加进了一阶的吉洪诺夫(Tikhonov)正则化方案[15],改进为三维时域微波断层成像算法;进而运用FDTD法和Polak-Ribière-Polyak(PRP)非线性共轭梯度(conjugate gradient,CG)法[12],对一个数值算例进行迭代计算,最后给出定量的相对介电常数和电导率分布图像。

2.成像方法

建立如图1所示的三维半球乳房模型和直角坐标系。乳房浸入无耗的匹配液体介质中。本文假设所有介质的电磁参数为各向同性,本构关系为线性,相对磁导率μr为1。

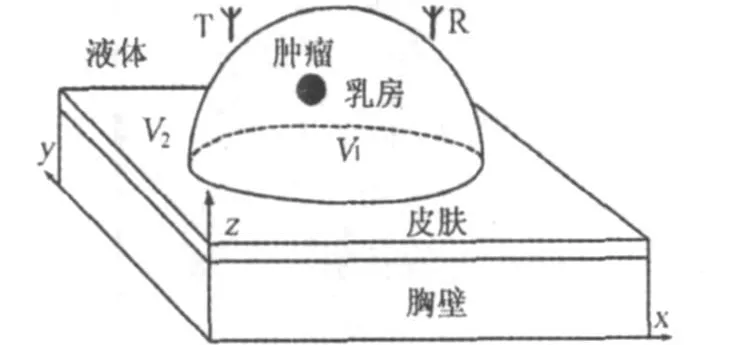
图1 三维半球乳房模型

图1 中,T和R分别表示收发分置(即双站)的发射和接收阵列天线[16],M根发射天线元和N根接收天线元分别位于r=r m和r=r n位置,其中m=1,2,…,M,n=1,2,…,N。这里,位置矢量r=(x,y,z)T,上标T表示转置(下文同)。依次激励其中的一根发射天线元,产生的电磁总场由N根接收天线元接收。

V 1表示待重建的乳房区域,V 2表示已知电磁参数的匹配液体和胸壁区域。整个区域的相对介电常数记为εr(r),电导率记为σ(r)。电参数分布进一步简记为

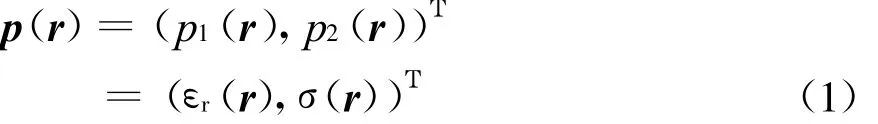
加在第m根发射天线上的激励源为

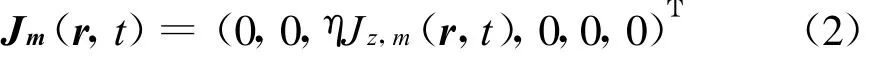
这里

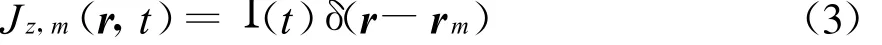
其中:δ是Dirac函数;Ι(t)为时间因子,自由空间的特征阻抗η=,其中 μ0和ε0分别为自由空间的磁导率和介电常数。产生相应的电磁场矢量um(p,r,t)满足算子方程

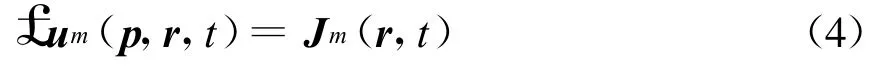
和初始条件

其中

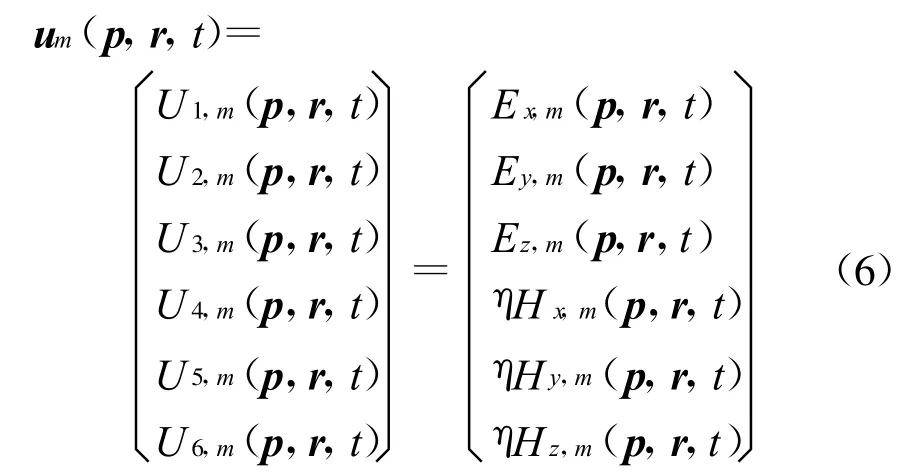
类似于文献[17],包含边界条件的偏微分算子£定义为

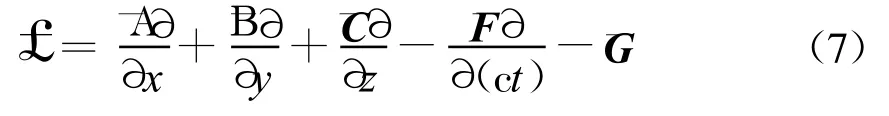
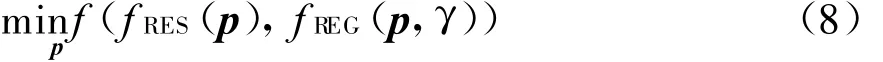
这里

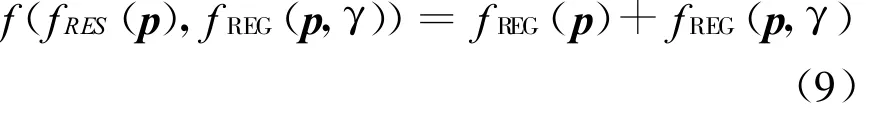
同时满足约束条件式(4)和(5)。

其中与剩余差有关的项为

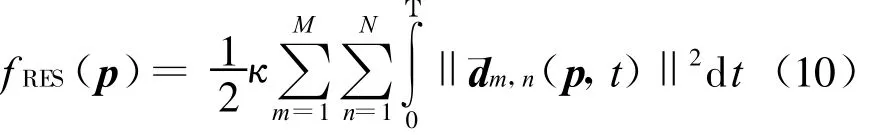
式中,剩余差为

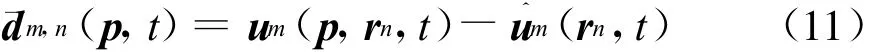
归一化因子为

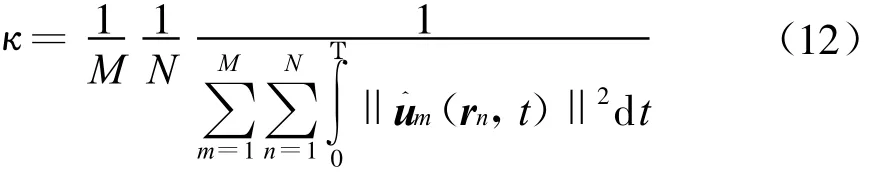
在Jm(r,t)激励下的时域测量场为

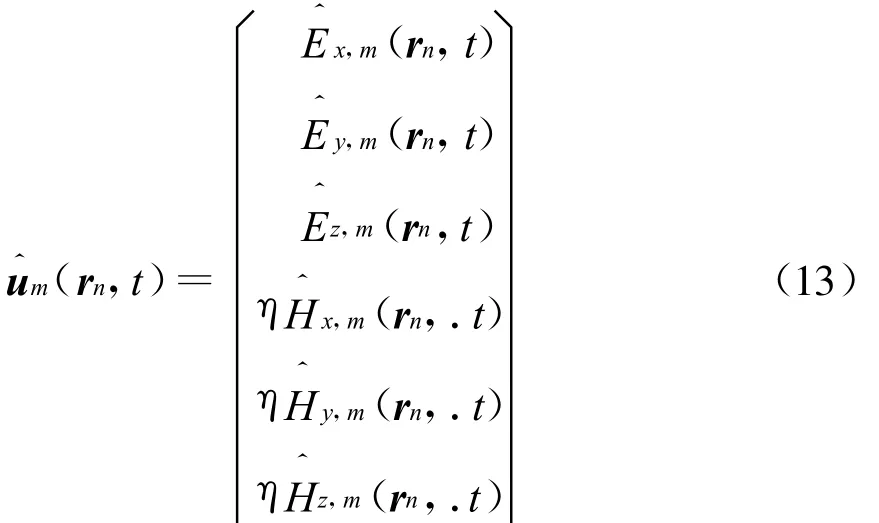
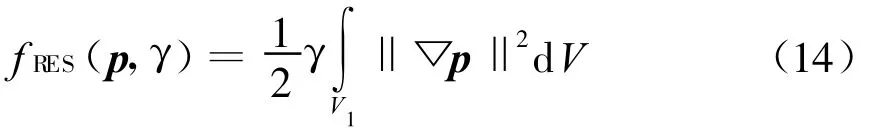
这里采用了一阶 Tikhonov正则化[15],γ为待定的正则化参数,▽为Hamilton算子。

引入Lagrange乘子罚函数

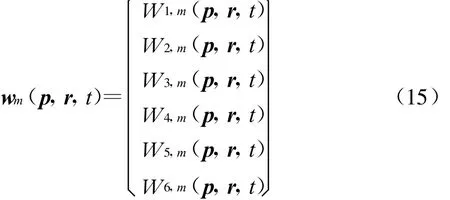
这里,r∈V1,t∈[T,0],这样,利用罚函数方法将原问题转化为无约束的优化问题。设 p*是原问题的解,且w m(p,r,t)是相应的 Lagrange乘子,由 Kuhn-Tucker定理[18]知,p*必是以下 Lagrange函数

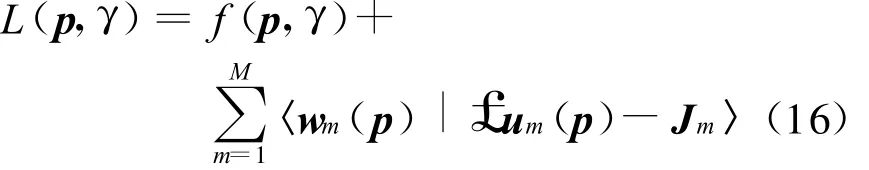
的稳定点,其必要条件是 Lagrange函数L的一阶变分δL|p=p*=0.

由于电磁场矢量u m(p,r,t)的时间t∈[0,T]是正演步进,而乘子罚函数wm(p,r,t)的时间t∈[T,0]是反演步进,这样不便于数值计算的统一实现。若对乘子罚函数w m(p,r,t)作时间变量替换tp=T-t,产生相应的函数 wpm(p,r,tp)。并经过一些计算[7],一方面,可以得到,wpm(p,r,tp)满足以下算子方程

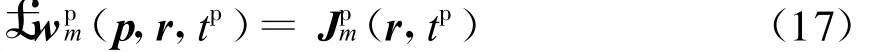
和初始条件

其中,tp∈[0,T],激励源为

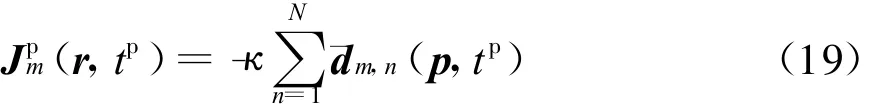
比较式(4)、(5)和(17)、(18),容易看出wpm(p,r,tp)和um(p,r,t)满足相似形式的偏微分算子方程,所不同的仅有激励源项,这样可以方便地利用相似的数值计算方法求解。另一方面,可以得到Lagrange函数L 关于p的Fréchet导数为

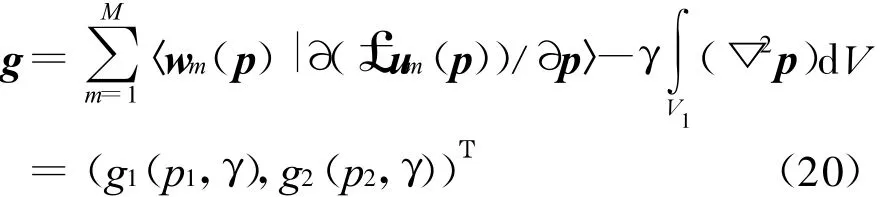
式中:

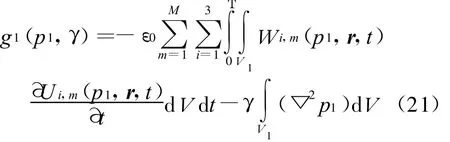
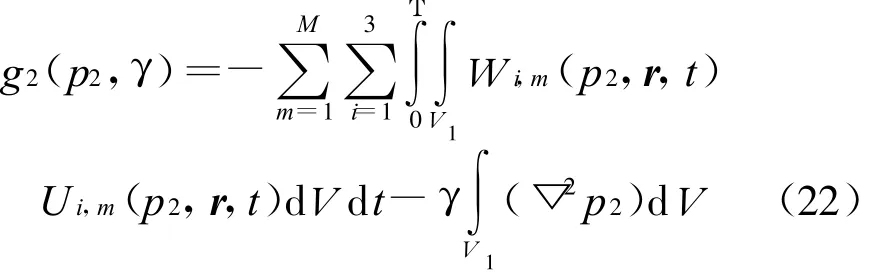
这样,有了闭式的Fréchet导数,本文的反演问题可以利用基于梯度的优化方法进行迭代处理。本文采用PRP非线性共轭梯度法[12]。设k表示迭代次数,这里,(k=0,1,…,kmax),kmax表示总共迭代计算次数,第k次迭代的估计特征参数分布为pk,则第k+1次迭代的更新公式为

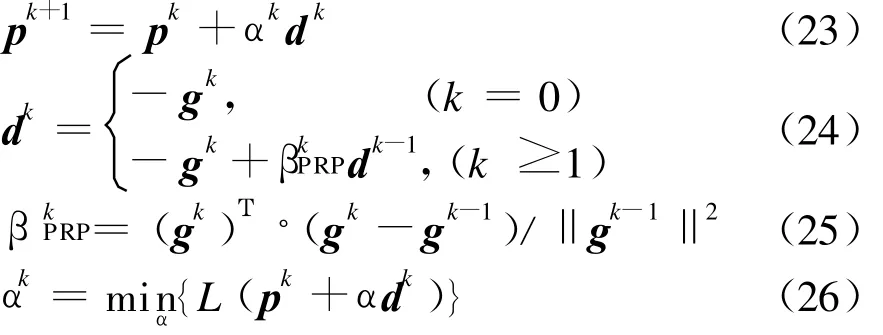
这里 ,gk、dk、βkPRP和αk分别为第k 次迭代的 Fréchet导数、搜索方向、标量因子和步长,其中步长αk可以通过求解线搜索问题式(26)得到[7]。

测量的电磁场u^m(r n,t)可以通过实验得到或者利用数值方法仿真代替,并且设定重建参数的迭代初值pk(k=0)以后,可以利用上述算法迭代求解重建参数pk,直到达到所需要的迭代次数或者计算精度为止。总结起来,三维时域微波断层成像算法的计算步骤如下:

①给定参数T、M、N、总共迭代次数k max或者阈值eps＞0以及入射脉冲 I(t),t∈[0,T],实验测量或者仿真计算场u^m(r n,t),其中t∈[0,T],m=1…M,n=1…N。

②初始化:取k=0,给定p0,仿真计算接收天线上的场u m(p0,r n,t)和成像区域的场u m(p0,r,t),其中,t∈[0,T],r∈V 1,m=1,…,M,n=1,…,N 。对(rn,t)和um(p0,rn,t)作时间变量替换t=T-tp,计算激励源Jpm(r n,tp),仿真计算成像区域函数wpm(p0,r,tp),作时间变量替换tp=T-t,得到成像区域的乘子罚函数 wm(p0,r,t),r∈V1。计算Fréchet导数 g0,计算搜索方向 d0,计算步长 α0。

③令k=k+1,更新估计参数pk,计算接收天线上的场um(pk,rn,t)和成像区域的场um(pk,r,t),其中,t∈[0,T],r∈V 1,m=1,…,M,n=1,…,N。

⑤计算Fréchet导数 gk,如果‖gk‖ ≤eps或者k=则停;否则进入下一步。

⑥计算标量因子βkPRP和搜索方向dk.

⑦计算步长αk,转③步。

3.仿真算例

为了验证本文成像算法的性能,数值算例中,取乳房半球的半径为50 mm,外表2 mm厚为皮肤层,其余为脂类乳房组织。胸壁厚为30 mm,未被乳房覆盖的表层也接2 mm厚的皮肤层。设乳房组织中含有两个半径均为3 mm的球状肿瘤1和2。肿瘤1的中心坐标分别为x1=45 mm、y 1=70 mm和z1=45mm;肿瘤2的中心坐标分别为 x2=70 mm、y2=70 mm和z2=45 mm。

发射阵列天线取最简单的情形,只有1根天线元,即M=1,贴在乳房顶部放置。接收天线阵列按照乳房高度均分5层,由上向下分别在乳房表面圆周上均匀放置 4、5、6、7和 8根天线元,即 N=30。这里,我们忽略对天线元具体形状的建模,即分别视为发射和接收点。

激励源式(3)中的时间因子I(t)取为[19]

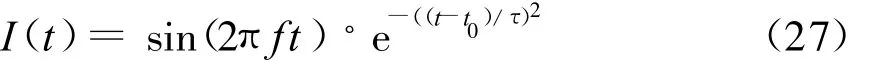
式中:τ=100 ps;t0=4·τ;中心频率 f=3.2 GHz。

在频率 f下,用于仿真测量数据的各种介质的电特性参数如表1所示[16]。

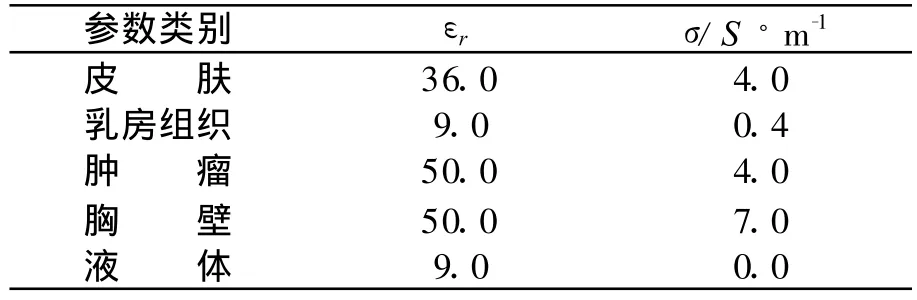
表1 介质的电特性参数

定义第k次迭代时,重建过程的相对剩余误差为[3]RREk

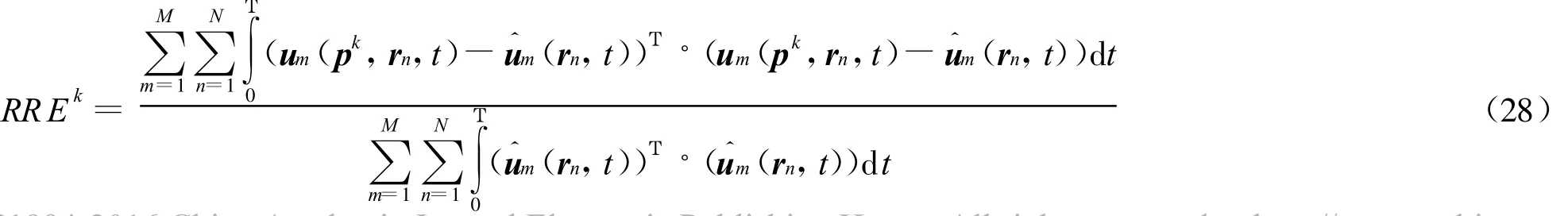
利用FDTD[13]法仿真计算代替测量电磁场u^m,每次迭代过程中,也用FDTD法计算u m和w m,取总共迭代次数kmax=50。计算空间离散化时,Yee元胞尺寸取为Δ=1 mm×1 mm×1 mm,时间采样步长为 Δt=Δ/(2·c),整个计算空间在 x、y和z方向剖分的元胞数目分别为140、140和90,周围用8层完全匹配层(perfectly matched layer,PML)吸收边界截断[13]。观测时间取为 T=500·Δt。

成像的目标是重建乳房区域的电参数分布,k=0时,迭代计算的初值p0取等于均匀乳房组织的相应特征参数。

在实际的测量中一般存在噪声污染,本文假定,在仿真的测量数据中加入均匀分布的随机噪声,其信噪比定义为[17]

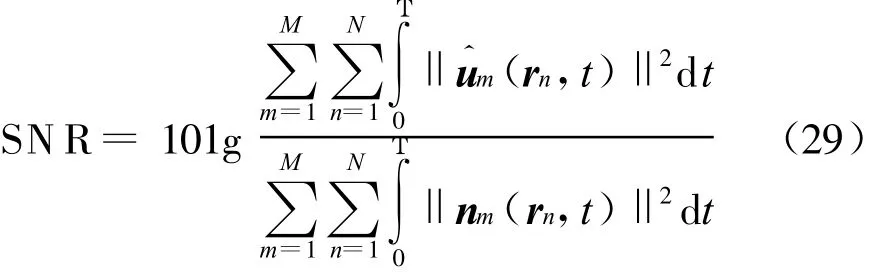
另外,在真实的乳房组织中还存在乳腺导管和小叶等组织,它们降低了肿瘤的检测效果,为了考察它们对反演算法的影响,取乳房组织的电特性参数在正常值的1±10%倍范围内均匀随机变化[14]。

为了对抗噪声污染和降低反演的病态性质,避免求解结果限于局部最优,这里加入一阶的吉洪诺夫正则化,正则化参数取γ=0.001[7]。

通过肿瘤1和2中心的x-y横截面、通过肿瘤1和2中心的 x-z横截面和通过肿瘤2中心的y-z横截面上得到的εr分布分别如图2、3和 4所示;通过肿瘤 1和 2中心的x-y横截面、通过肿瘤1和2中心的 xz横截面和通过肿瘤2中心的 y-z横截面上得到的σ分布分别如图5、6(见 1234页)和7所示 。其中各子图(a)、(b)、(c)和(d)分别表示相应电参数的真实分布以及在迭代次数分别为k=0、25、50时的重建结果。为了检验成像方法检测肿瘤的效果,各子图(d)中附加的黑色圆周表示真实肿瘤的轮廓。

图8给出相对剩余误差随迭代次数的变化关系。其中,第25和50次迭代的相对误差分别为4.6×10-2%和4.2×10-3%。

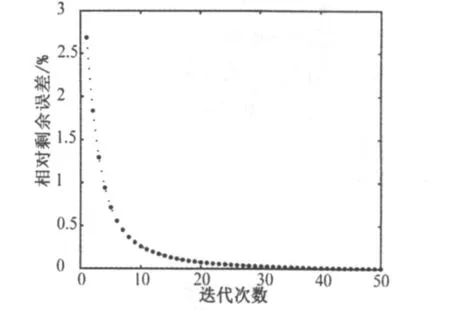
图8 不同迭代次数的相对剩余误差

比较图2～8,经过分析发现:1)从总体来看,算法是收敛的,收敛速度先快后慢。随着迭代次数的增加,相对误差逐渐减小,重建精度逐渐提高。当然,迭代次数越高,计算时间也越长,实际的工程应用中,可以选择一个重建精度与实时重建的合理折中。2)皮肤、肿瘤和乳房组织的电特性参数差异较大,是主要的散射体。迭代次数k=50时,σ分布收到了较好的重建效果,较好地重现了它们的形状、尺寸、位置。然而,εr分布和真实值尚有较大的差异,适当增加仿真时间步数或者适当加大迭代次数可以适当改善重建结果。3)对比皮肤和肿瘤,前者比后者的重建效果好;对比肿瘤1和肿瘤2,后者的重建效果不如前者。其原因是肿瘤比起皮肤位于较深位置,而且肿瘤2位于更深位置,距离天线较远,信号在乳房组织中经受衰减,来自肿瘤2的散射信号较弱所致,解决方法是适当降低激励源的频率。当然这也同时降低了重建的分辨率,在实际的工程应用中,应该选择一个检测深度和重建分辨率的合理折中,即选择一个合理的激励频率。

综合起来,尽管由于测量视角的受限和测量数据的有限增加了反演问题的病态性质,但是在噪声环境下,在电特性参数取正常值的1±10%倍均匀随机变化的乳房组织中,肿瘤目标仍被成功地探测。这可能得益于算法的鲁棒性和正则化方案改善了逆问题的病态性质。当然,正则化方案已有多种,正则化参数的选择也是个困难的问题,最优的正则化参数一般需要根据具体问题多次数值测试确定。

4.结 论

为了提高成像的分辨率,常利用高频宽带脉冲进行生物异常体检测,在时域进行微波断层成像是一种重要的生物医学成像方法。用它进行早期的乳腺癌检测具有良好的应用前景和重要的现实意义。

本文应用泛函分析和变分法,改进了拉格朗日乘子算法并得到闭式的Lagrange函数关于重建参数的Fréchet导数,采用了一阶的 Tikhonov正则化方案。在噪声环境下,利用FDTD法和PRP非线性CG法对三维半球乳房模型进行了仿真测试,介电常数和电导率分布图像均被定量地获得,散射体的位置、尺寸和形状等目标信息得以成功地再现。电导率和介电常数双参数反演方法的研究,丰富了宽带高频电磁脉冲在有耗介质里的传播理论,使得电磁勘探方法的反演解释方法得到一般化,具有一定的理论意义。初步的结果证实了改进后的时域微波断层成像方法检测乳腺癌的可行性和有效性,表明了正则化方案对反演问题的病态性质起到了一定的抑制作用,为工程应用研究奠定了良好的理论基础。

当然,本文的时域微波断层成像算法并不局限于乳腺癌检测,也可应用到目标识别、地球物理勘探和遥感等一般的电磁逆散射问题中。另外,生物肌体组织一般是频率色散介质,特别是对超宽带微波检测,色散效应有重要影响[20],相关问题将另文讨论。

[1] 刘广东,张业荣.An overview of active microwave imaging for early breast cancer detection[J].南京邮电大学学报(自然科学版),2010,30(1):64-70.

LIU Guangdong,ZHANG Yerong.An overview of active microwaveimaging for early breast cancer detection[J].Journal of Nanjing University of Posts and Telecommunications(Natural Science),2010,30(1):64-70.(in Chinese)

[2] 田雨波,钱 鉴.微波近场成像检测乳腺癌及其微波热疗[J].微波学报,2003,19(3):72-78.

TIAN Yubo,QIAN Jian.Breast cancer detection based on microwave near field imaging and its microwavehyperthermia[J].Journal of Microwaves,2003,19(3):72-78.(in Chinese)

[3] 张业荣,聂在平,阮颖铮.用变形玻恩迭代法反演电导率的二维非均匀分布[J].电子学报,1997,25(12):100-111.

ZHANG Yerong,NIE Zaiping,RUAN Yingzheng.Inversion of two-dimensional inhomogeneous conductivity distribution using the distorted born iterative method[J].Acta Electronica Sinica,1997,25(12):100-111.(in Chinese)

[4] TAKENAKA T,JIA H,TANAKA T.Microwave imaging of electrical property distributions by a forward-backward time-stepping method[J].J.Electromagn.Waves Appl.,2000,14(12):1609-1626.

[5] 徐伟强,王敏锡.用求解二维导体柱电磁逆散射[J].电波科学学报,2002,17(5):462-466.

XU Weiqiang,WANG Minxi.Electromagnetic inverse scattering of two-dimensional conducting objects by adaptive parameter real-coded genetic algorithm[J].Chinese Journal of Radio Science,2002,17(5):462-466.(in Chinese)

[6] 王文珂,黄卡玛,刘智明,等.遗传算法在生物组织电导率重构中的应用研究[J].电波科学学报,2003,18(4):400-403.

WANG Wenke,HUANG Kama,LIU Zhiming,et al.Study on conductivity reconstruction of biological tissue by using genetic algorithm[J].Chinese Journal of Radio Science,2003,18(4):400-403.(in Chinese)

[7] REKANOS I T.Time-domain inverse scattering using Lagrange multipliers:an iterative FDTD-based optimization technique[J].J.Electromagn.Waves Applicat.,2003,17(2):271-289.

[8] 邓小波,聂在平,赵延文,等.利用相位感应测井数据重建电导率和介电常数[J].电波科学学报,2005,20(2):236-240.

DENG Xiaobo,NIE Zaiping,ZHAO Yanwen,et al.Reconstruction of permittivity and conductivity using phase induction logging information[J].Chinese Journal of Radio Science,2005,20(2):236-240.(in Chinese)

[9] 傅 林,黄卡玛,向胜昭.生物组织磁聚焦电导率成像原理及反演算法[J].电波科学学报,2006,21(2):249-254.

FU Lin,HUANG Kama,XIANG Shengzhao.Focused magnetic fields conductivity tomography of biological tissue and its inverse algorithm[J].Chinese Journal of Radio Science,2006,21(2):249-254.(in Chinese)

[10]WINTERS D W,BOND E J,BARRY D V,et al.Estimation of the frequency-dependent average dielectric properties of breast tissueusing a time-domain inverse scattering technique[J].IEEE Trans.Antennas Propag.,2006,54(11):3517-3528.

[11] WINTERS D W,SHEA J D,KOSMAS P,et al.Three-dimensional microwave breast imaging:dispersive dielectric properties estimation using patientzaspecific basis functions[J].IEEE Trans.Med.Imag.,2009,28(7):969-981.

[12] DAI Yuhong.A family of hybrid conjugate gradient methods for unconstrained optimization[J].Math.of Computation,2003,17(2):1317-1328.

[13] TAFLOVE A,HAGNESSS C.Computational Elec-trodynamics:The Finite-Difference Time-Domain Method[M].3rd ed.Norwood,MA:Artech House,2005.

[14] JOHNSON J E,TAKENAKA T,TANAKA T.Two-dimensional time-domain inverse scattering for quantitative analysis of breast composition[J].IEEE Trans.Biomed.Eng.,2008,55(8):1941-1945.

[15] TIKHONOV A N,ARSENIN V T.Solutions of Ill-Posed Problems[M].Washington,D.C.:Winston,1977.

[16] XIE Yao,GUO Bin,XU Luzhou,et al.Multistatic adaptive microwave imaging for early breastcancer detection[J].IEEE Trans.Biomed.Eng.,2006,53(8):1647-1657.

[17] TAKENAKA T,ZHOU H,TANAKA T.Inverse scattering for a three-dimensional object in the time domain[J].J.Opt.Soc.Am.A,2003,20(10):1867-1874.

[18] KUHN H W,TUCKER A W.Nonlinear Programming[M].Berkeley,California,University of California Press,1951:481-492.

[19] ZHOU Beibei,SHAO Wenyi,WANG Gang.The application of multi-look in UWB microwave imaging for early breast cancer detection using hemispherical breast model[C]∥IEEE EMBS,2005:1552-1555.

[20] 刘广东,张业荣.二维有耗色散介质的时域逆散射方法[J].物理学报,2010,59(10):6966-6976.

LIU Guangdong,ZHANG Yerong.Time-domain inverse scattering problem for two-dimensional frequency-dispersive lossy media[J].Acta Phys.Sin.,2010,59(10):6966-6976.(in Chinese)