基于双平行线阵的相干分布源二维DOA估计

郑 植 李广军 滕云龙

(1.电子科技大学电子科学技术研究院,四川成都611731;2.电子科技大学通信与信息工程学院,四川成都611731)

1.引 言

分布式信源波达方向(DOA)估计是现代通信信号处理领域中的一个研究热点。无线通信系统的电波传播有直达波传播和非直达波传播[1]两种方式。在直达波传播情形下,移动台和接收阵列之间存在直线路径,因此,一般将目标信号假设为点源。而在非直达波传播情形下,由于本地多径散射将导致信号在到达接收阵列时发生一定程度的角度扩展。此时,传统的点源假设及其对应的参数估计算法将不再适用,必须采用分布源模型及其相应的参数估计算法。

分布源一般可分为相干和非相干两种类型。迄今为止,针对上述两种分布源模型已发展了多种DOA估计算法[2-10]。其中,较为著名的有DSPE[2]、DISPARE[3]、最大似然[4]、协方差匹配[5]和广义Capon波束形成法[6]。但以上方法均针对的是一维分布源。对于二维分布源,对应的DOA估计算法相对较少。其中,文献[11-14]利用L型线阵或均匀圆阵,提出了几种相干分布源二维DOA估计算法。这些算法均把四维参数估计问题转化为两个二维参数估计问题来处理,在一定程度上降低了算法的复杂度,但仍需二维搜索。文献[15]利用双均匀圆阵提出了一种估计相干分布源二维中心DOA的一维交替搜索(SOS)算法,该算法把二维搜索问题简化为一维搜索问题,进一步降低了复杂度。文献[16]提出了一种无需搜索的算法,但仍需对样本协方差矩阵做特征分解,计算复杂度依然较高。文献[17]给出的算法不需要谱搜索和对样本协方差矩阵特征分解,但没有解决参数配对问题,不能用于多源场合。

本文研究相干分布源的二维DOA估计问题。基于双平行均匀线阵,提出了一种低复杂度的估计算法。该算法充分利用了双平行线阵的结构特点,通过将平移子阵的广义方向矢量化为分布源中心DOA的解耦形式获得阵列间的旋转不变矩阵,并利用一种改进的传播算子法求解旋转不变矩阵,进而最终估计出分布源的二维中心DOA。本文算法不需要谱搜索和对样本协方差矩阵特征分解。和常规算法相比,计算复杂度更低。而且算法给出了详细的参数配对流程,能够处理多个分布源。本文算法估计性能良好,在小角度扩展下其估计性能和SOS算法很接近。此外,算法与分布源的角分布形式无关,稳健性好。

2.信号模型

考虑图1所示的阵列结构,它由两个平行的均匀线阵X和Y组成。其中阵列X有M+1个阵元,阵列Y有M个阵元且与X的距离为d。各阵列的阵元间距也为d。假设远场空间中有D个窄带相干分布源以不同的二维中心波达方向(θi,φi)(i=1,…,D)入射到阵列,其中θi和φi分别表示第i个分布源的中心方位角和中心俯仰角(θi∈[-π/2,π/2], φi∈[0,π/2],σθi和 σφi为对应的角度扩展参数 。设各阵元的噪声为加性高斯白噪声,且与信号不相关。

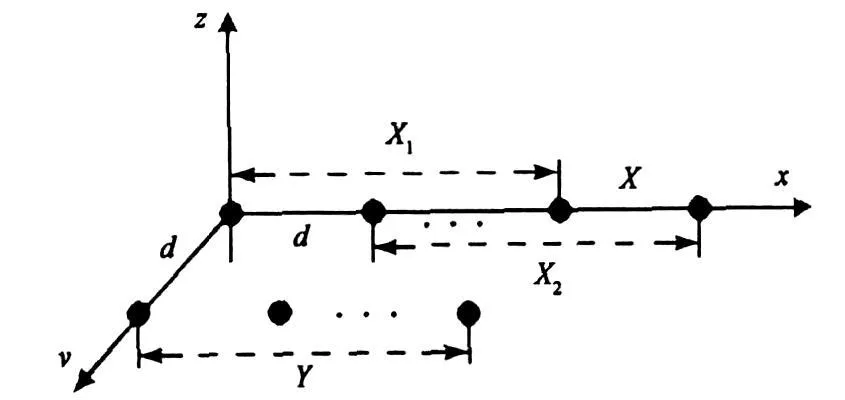
图1 双平行均匀线阵结构

在t时刻,阵列X和Y的观测数据可表示为

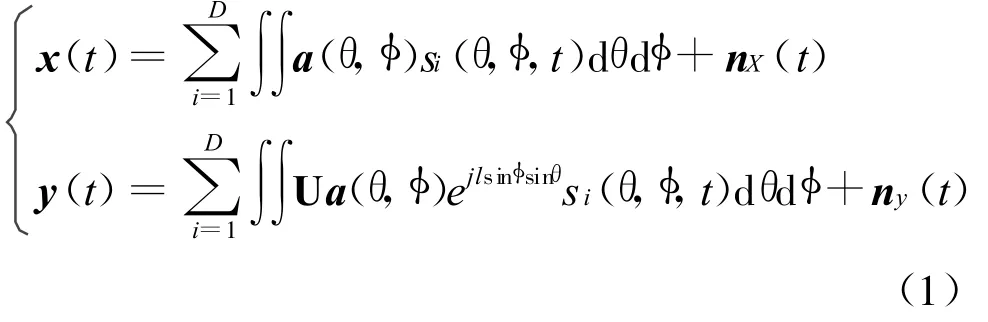
式中 :a(θ,φ)=[1,ejlsinφcosθ,…,ejlMsinφcosθ]T为点源方向矢量;l=2πd/λ(λ为信号波长);U=[I M×M|0M×1]为数据选择矩阵;si(θ,φ,t)为第 i个分布源的角信号密度函数。

对于相干分布源,角信号密度函数可写为

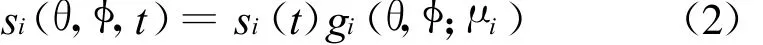
式中:gi(θ,φ;μi)为确定性角信号分布函数;μi=[,σθi,φi,σφi]为角度参数向量 。

定义阵列X和Y的广义方向矢量如下

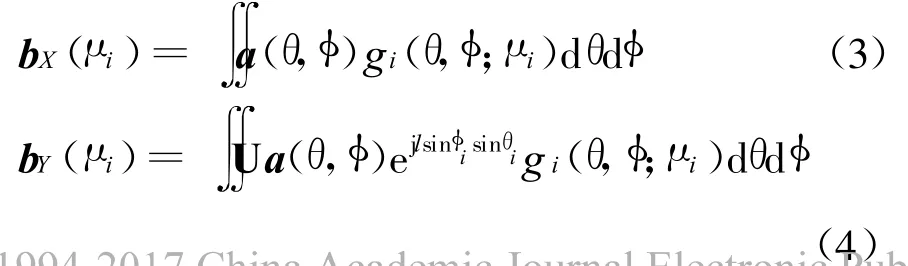
则式(1)可写成矢量形式

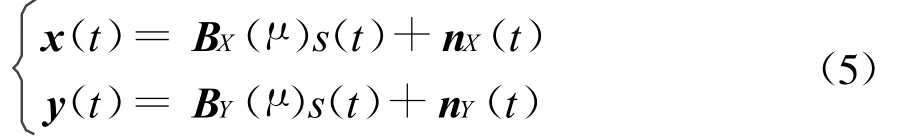
式中:B X(μ)是(M+1)×D维广义方向矩阵;B Y(μ)是M×D维广义方向矩阵。

如图1所示,将X划分成子阵X1和X2,则X1和X2的广义方向矢量可定义为

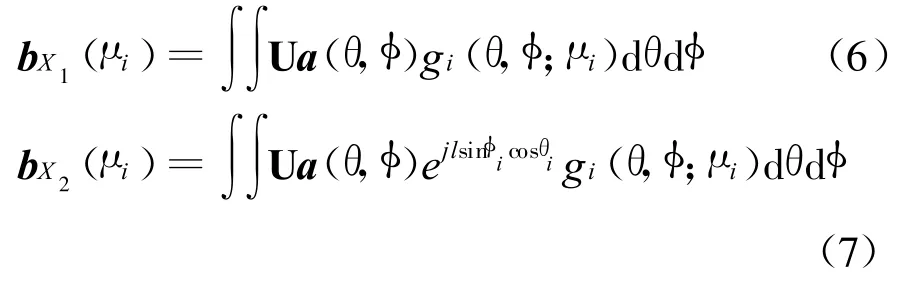
对任意的二维方向(θ,φ),定义 θ=θi+～θ和 φ=φi+～φ。在小角度扩展下,将a(θ,φ)的第k个元素在中心方向(θi,φi)处做一阶泰勒近似

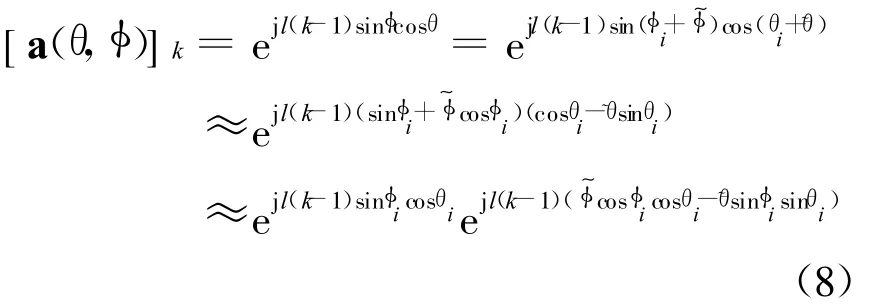
将式(8)代入式(6),可得中心DOA的解耦形式

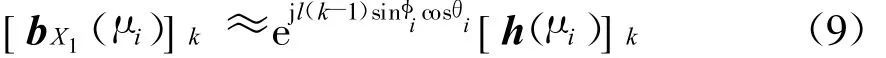
式中

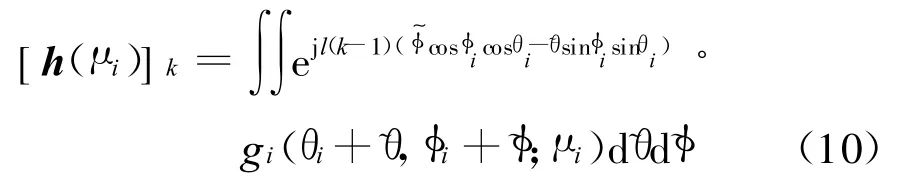
将式(8)代入式(7),可得

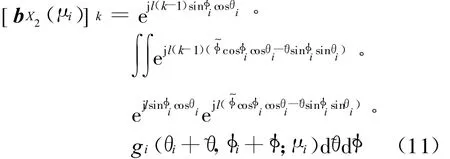
由于ejl(～φcosφicosθi-～θsinφi sinθi)≈1,则式(11)可重写为

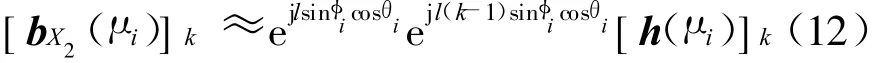
由式(9)和式(12),可得如下关系

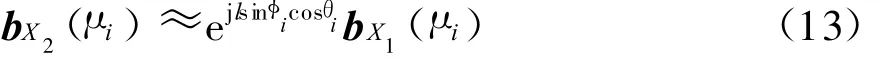
用矩阵表示

式中:B X1(μ)均为M×D维的广义方向矩阵;ΦX=diag[ejlsinφ1cosθ1,…,ejlsinφDcosθD].

同理,将式(8)代入式(4),可得

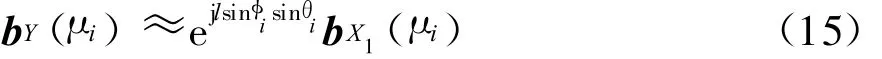
用矩阵形式表示

式中:B Y(μ)为M×D维广义方向矩阵;旋转矩阵ΦY=diag[ejlsinφ1sinθ1,…,ejlsinφDsinθD].

将阵列X和Y的观测数据合并为

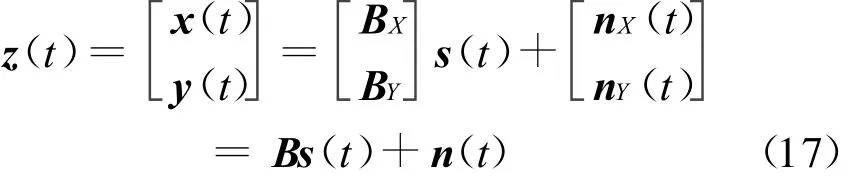
式中:B=[BTX,BTY]T为总阵列的广义方向矩阵;n(t)=[nTX(t),nTY(t)]T,为总阵列的噪声矢量。

3.算法描述

传播算子法在点源的DOA估计中已有不少应用。其中,文献[18]的方法利用传播算子法构建谱搜索函数估计DOA参数,复杂度较高。文献[19][20]的方法虽不需要进行谱搜索,但存在较大的阵列孔径损失,估计精度不高。此部分针对相干分布源,充分利用双平行线阵的结构特点,提出了一种基于传播算子的二维中心DOA估计算法,该算法无需谱搜索,也无任何阵列孔径损失,估计精度较高。

3.1 传播算子的估计

假设总阵列的广义方向矩阵B是列满秩的,则B中有D行是线性独立的,其它行可由这D行线性表示。假设B的前D行线性独立,则B可分为

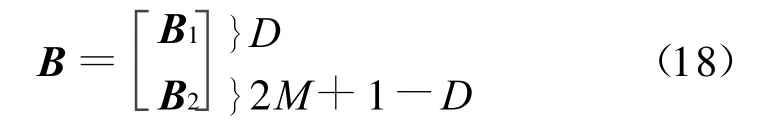
式中,B1和B2分别为D×D 维和(2M+1-D)×D维矩阵。

传播算子定义为由2M+1-D维复空间C2M+1-D到D维复空间CD的唯一线性算子P,且P满足

由于传播算子P的估计需要用到分布源的方位信息,故可由总阵列接收数据的数据协方差矩阵Rzz=E[z(t)zH(t)]求解,具体步骤如下

①估计协方差矩阵R zz

式中,N为阵列接收的快拍数。

式中,G和H分别为(2M+1)×D和(2M+1)×(2M+1-D)维矩阵。

③最小化下面的代价函数

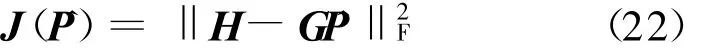
式中,‖·‖2F表示Frobenius范数。其解为

3.2 基于传播算子的分布源二维DOA估计方法

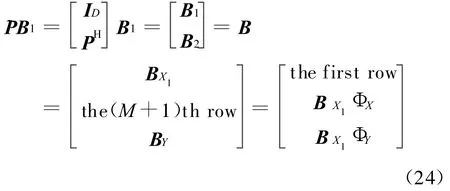
也即由～P张成信号子空间。将 ～P按行划分成三个矩阵,其中第1到第M行记为～P1,第2到第M+1行记为～P2,第 M+2到第2M+1行记为 ～P3,如下所示

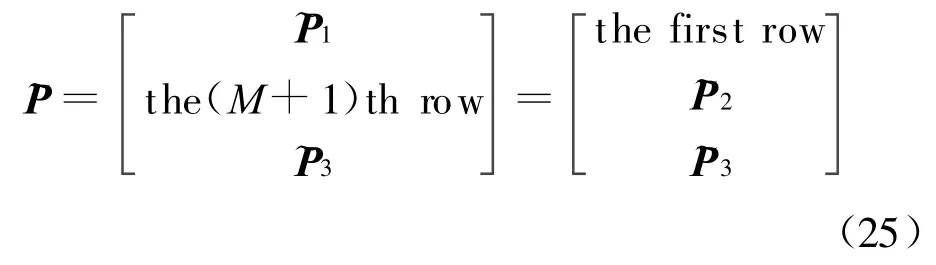
由式(24)和式(25),可得

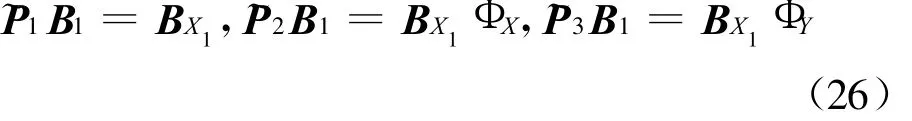
由式(26),可得

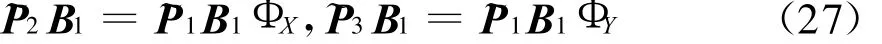
进而有

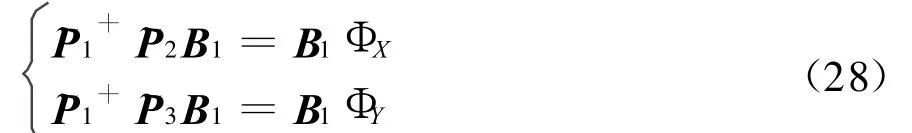
式中,[·]+表示求广义逆矩阵,且～P1+=(～P1H～P1)-1～P1H。令 ～P1+～P2=ΨX,～P1+～P3=ΨY,分别对 ΨX和 ΨY进行特征分解,即可求出 ΦX和 ΦY。对于单一分布源情形,由 ΨX和 ΨY的唯一特征值 ξxi和 ξyi通过式(29)和(30)即可估计出分布源的中心方位角和中心俯仰角。

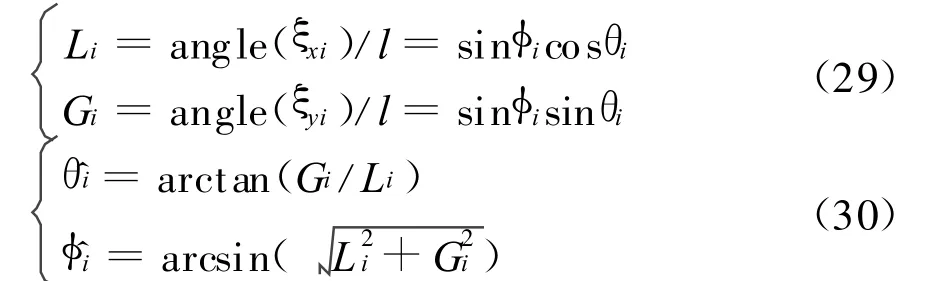
式(29)中,angle(·)表示取相位运算。

对于多个分布源的情况,首先需要对特征值进行配对,否则不能得到正确的估计结果。根据阵列的结构特点,这里用文献[21]中的方法来完成特征值的配对。

若对 ΨX进行特征分解得到的特征值和对应的特征向量分别为ξxi和U i.因为 ΨX和 ΨY有相同的特征向量,所以U i也是 ΨY的特征向量。假设 ΨY与特征向量U i对应的特征值为ξyi,则由矩阵、特征值和对应特征向量之间的关系,可得

令

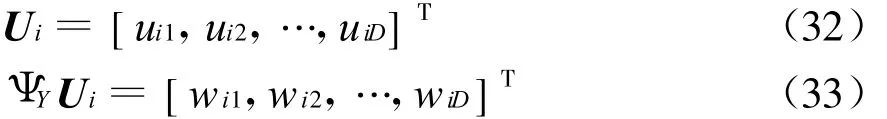
根据式(31)～(33),可得

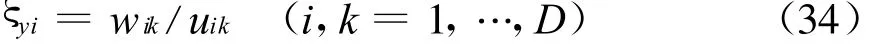
为了提高估计精度,可对式(34)进行如下修正

至此,即求出一一对应的ξyi和ξxi。然后利用式(29)和(30)即可正确估计出每个分布源的二维中心DOA。

3.3 计算复杂度分析

SOS算法是一种典型的一维搜索算法。其计算量主要集中在估计样本协方差矩阵,对样本协方差矩阵进行特征分解和一维谱搜索上。估计样本协方差矩阵并对其进行特征分解所需的计算量约为o(4M2N+8M3),而谱搜索的计算花费跟搜索的精度有关,做精细搜索时一般都在o(M6)以上。文献[16]是一种典型的无需谱搜索的算法,它的计算量主要体现在估计两个样本协方差矩并对其做特征分解上,所需的总计算量约为o(5M2N+9M3)。而本文算法的计算量主要体现在估计一个2M+1阶的样本协方差矩阵和对两个D阶矩阵 ΨX和ΨY的特征分解上,需要的总计算量约为o((2M+1)2N+2D3)。显然,本文算法的计算量比SOS算法和文献[16]算法都低。

4.仿真实验与分析

此部分通过3个统计实验来考察算法的性能。实验基于图1所示的阵列结构。其中,M=8,d=0.5λ。

实验1:比较本文算法和SOS算法(其中,每个圆阵的阵元数为8,两圆阵间距0.1倍波长)的性能。考虑一个相干分布源入射到阵列,其角分布为高斯分布 ,μi=[-30°,2°,60°,2°] 。图 2 表示在快拍数为 400的条件下,在不同的信噪比处分别做200次Monte-Carlo实验得到的二维DOA估计的均方根误差(RMSE)随信噪比(SNR)变化的曲线。从图2可以看出,本文算法在不同信噪比处的估计性能非常接近于SOS算法。图3表示在SNR=10 dB的条件下,以不同的快拍数分别进行 400次Monte-Carlo实验得到的二维DOA估计的均方根误差随快拍数变化的曲线。从图3可以看出,本文算法在相同快拍数时的估计精度略高于SOS算法。这里,二维DOA估计的均方根误差定义为

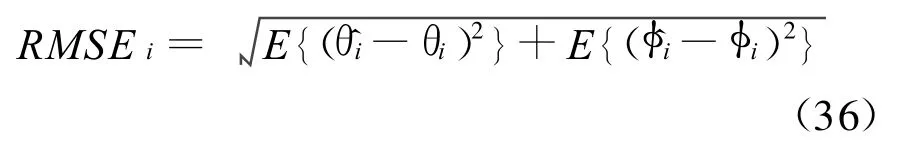
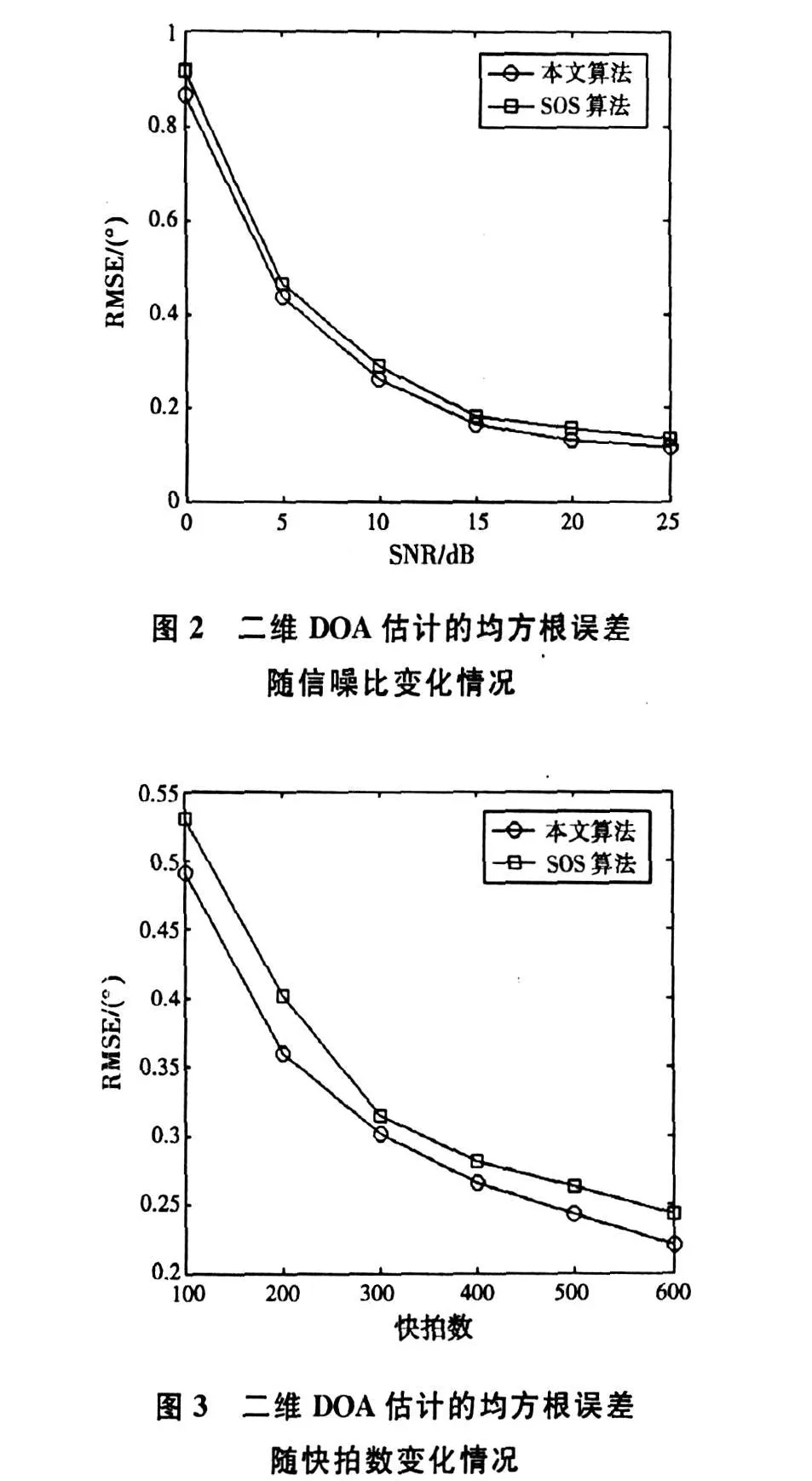
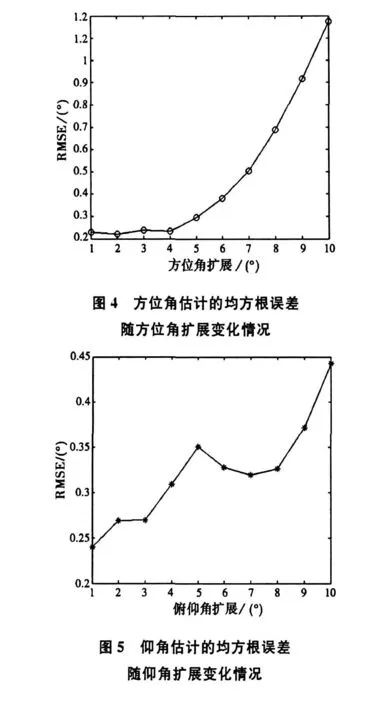
实验2:考察角度扩展大小对算法估计性能的影响。分布源的角分布情况与中心DOA参数与实验 1 相同 。当 σφi=2°,在 SNR=10 d B,快拍数为200的条件下,以不同的方位角扩展进行500次Monte-Carlo实验,得到图4所示的方位角估计的均方根误差随方位角扩展变化的曲线。同样,当σθi=2°,做类似的实验,得到图5所示的仰角估计的均方根误差随仰角扩展变化的曲线。从图4可以看出,方位角扩展越小,方位角估计的均方根误差变化越小。而随着方位角扩展增加,方位角估计的均方根误差急剧增加。类似的情况也可从图5中看到。以上说明算法在小角度扩展情形下估计性能更好。

实验3:考察算法估计多个不同角分布信号的能力。考虑两个相干分布源入射的情况。其中一个分布源是高斯分布源(GCD Source),其角度参数为μ1=[-50°,2°,10°,2°]。另一个分布源是均匀分布源(UCDSource),其角度参数为μ2=[40°,2°,75°,1°] 。在快拍数为800的条件下,以不同的信噪比分别进行500次Monte-Carlo实验,得到图6所示分布源二维DOA估计的均方根误差随信噪比变化的曲线。从图6可以看出,本文算法能够有效估计多个分布源,且无需知道分布源的角分布函数形式。

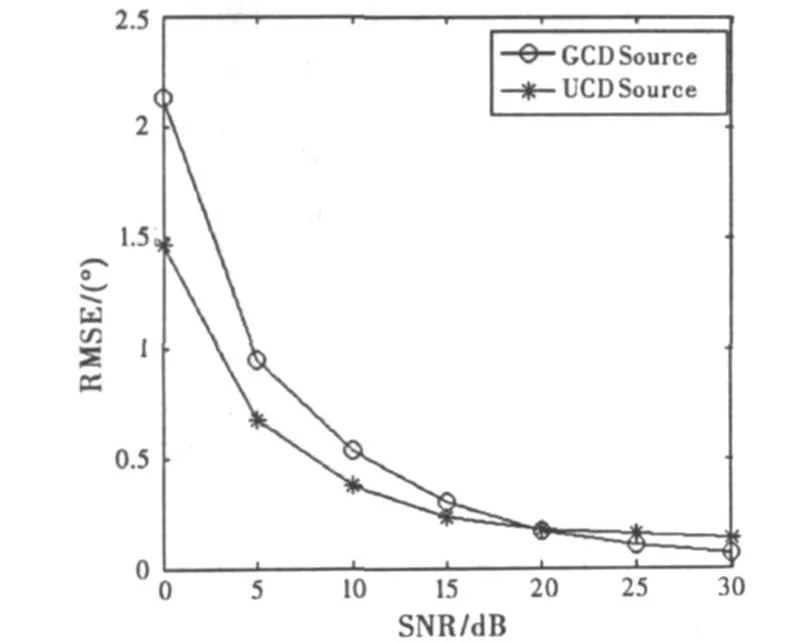
图6 二维DOA估计的均方根误差随信噪比变化情况

5.结 论

利用两个平行线阵,本文提出了一种低复杂度的相干分布源二维DOA估计算法。本文算法无需谱搜索和对样本协方差矩阵做特征分解,计算复杂度很低,易于实时处理和工程实现。仿真结果表明:在小角度扩展条件下,本文算法估计性能良好,接近于SOS算法。而且算法无需知道分布源角分布函数的先验信息,具有一定的稳健性。

[1] TAKADA J,JIYE F,HOUTAO Z.Spatio-temporal channel charact-erization in a suburban non line-ofsight microcellular environment[J].Selected Areas in Communications,IEEE Journal on.2002,10(3):532-538.

[2] VALAEE S,CHAMPAGNE B,KABAL P.Parametric localization of distributed sources[J].IEEE Trans Signal Process,1995,43(9):2144-2153.

[3] MENG Y,STOICA P,WONG K M.Estimation of the direction of arrival of spatially dispersed signals in array processing[J].IEE Proceedings-Radar,Sonar and Navigation,1996,143(1):1-9.

[4] MENG Y,WONG K M,WU Q.Estimation of thedirection of arrival of spread source in sensor array processing[C]//Proc.ICSP,1993,10:430-434.

[5] SHALLBAZPANAHI S,VALAEE S,GERSHMAN A B.A covariance fitting approach to parametric localization of multiple incoherently distributed sources[J].IEEE Transactions on Signal Processing,2004,52(3):592-600.

[6] HASSANIEN A,SHALLBAZPANAHI S,GERSHMAN A B.A gereralized Capon estimator for loealization of multiple spread sources[J].IEEE Trans.on Signal Proeessing,2004,52(l):280-283.

[7] 万 群,杨万麟.一种分布式目标波达方向估计方法[J].通信学报,2001,22(2):65-70.

WAN Qun,YANG Wanlin.A approach to direction of arrival estimation of distributed sources[J].Journal of China Institute of Communications,2001,22(2):65-70.(in Chinese)

[8] 张林让,田 惠,李 燮.分布式目标参数估计的波束域处理方法[J].电波科学学报,2004,19(1):87-91.

ZHANG Linrang,TIAN Hui,LI Xie.The beamspace method for parameters estimation of distributed sources[J].Chinese Journal of Radio Science,2004,19(1):87-91.(in Chinese)

[9] 钱 斌,杨万麟,万 群.一种利用旋转结构的分布式信号DOA估计方法[J].电波科学学报,2007,22(4):702-706.

Qian Bin,Yang Wanlin,WAN Qun.A approach to DOA estimation of distributed signals using rotational invariance structure[J].Chinese Journal of Radio Science,2007,22(4):702-706.(in Chinese)

[10] 熊维族.一种盲的多个分布源到达方向估计算法[J].电波科学学报,2008,23(5):942-945.

XIONG Weizu.A blind DOA estimation algorithm for multiple spread sources[J].Chinese Journal of Radio Science,2008,23(5):942-945.(in Chinese)

[11] LEE S R,SONG I,CHANG T,et al.Distributed source location estimation using acircular array[C]//ISSPA,1996:341-344.

[12] LEE S R,SONG I,LEE Y U,et al.Estimation of distributed elevation and azimuth angles using linear arrays[C]//MILCOM,1996:868-872.

[13] WAN Q,PENG Y N.Low-complexity estimator for four-dimensional parameters under a reparameterised distributed sourcemodel[J].IEE Proc.Radar,Sonar Navigation,2001,148(6):313-317.

[14] WAN Q,YANG W L.Low-complexity estimator for two-dimensional DOA under a distributed source model[C]//CIE Radar.Beijing,2001:814-818.

[15] LEES R,SONG I,KWON H,et al.Low-complexity estimation of 2D DOA for coherently distributed sources[C]//Signal Proeessing,2003,83:1789-1802.

[16] GUO X S,WAN Q,YANG W L,et al.Low-complexity 2D coherently distributed sources decoupled DOAs estimation method[J].Sci China Ser F-Inf Sci,2009,52(5):835-842.

[17] 韩英华,汪晋宽,宋 昕.相干分布式信源二维波达估计算法[J].电子与信息学报,2009,31(2):323-326.

HAN Yinghua,WANG Jinkuan,SONG Xi.2D DOA estimation algorithm for coherently distributed source[J].Journal of Electronics&Information Technology,2009,31(2):323-326.(in Chinese)

[18] MARCOS S,MARSA 1A,and BENIDIR M.The propagator method for source bearing estimation[J].Signal Processing,1995,42(2):121-138.

[19] MARSAL A,MARCOS S.A reduced complexity ESPRIT method and its generalization to an antenna of partially unknown shape[C]//ICASSP,1994,4:29-32.

[20] 吴云韬,廖桂生,田孝华.一种波达方向、频率联合估计快速算法[J].电波科学学报,2003,18(4):380-384.

WU Yuntao,LIAO Guisheng,TIAN Xiaohua.Fast algorithm for joint direction-of-arrival and frequency estimation[J].Chinese Journal of Radio Science,2003,18(4):380-384.(in Chinese)

[21] 刁 鸣,缪善林.一种二维ESPRIT算法参数配对新方法[J].系统工程与电子技术,2007,29(8):1226-1229.

DIAO Ming,MIAO Shanlin.New method of parameter matching for 2-D ESPRIT algorithms[J].Systems Engineering and Electronics,2007,29(8):1226-1229.(in Chinese)