UWB雷达杂波物理建模与仿真分析

杨利民 许志勇 苏卫民 顾 红

(南京理工大学电子工程与光电技术学院,江苏 南京210049)

1.引 言

UWB雷达是指相对带宽不小于 25%的雷达[1],相对带宽定义为2(fH-fL)/(fH+fL),通常情况下UWB雷达具有很高的距离分辨力。杂波是指雷达接收机接收的不感兴趣的回波[2],通常用σ0来描述。虽然UWB雷达分辨率高,具有良好的杂波抑制能力,但在雷达设计的分析阶段,以及在优化阶段,当无法获取测试数据时,杂波的建模和仿真依然具有重要的指导意义。

由于杂波具有随机性,通常利用统计特性进行描述[3-4]。采用统计模型的另一原因是传统的目标检测理论基于杂波的统计特性来判断是否存在目标。但像UWB雷达这样的高距离分辨率雷达,该模型不再服从如Rayleigh分布之类的典型短拖尾[4]。此外,杂波统计模型物理特性不明显,建立的杂波模型不能直接反映测量区域的地形变化特征。另常用杂波建模方法是反映地表面变化特征的物理建模。文献[5]中视测量区由不同的平板组合而成(表面由许多小且方向不同的小平板组合),以简化复杂地貌。每块小平板的反射方向图可视为等尺寸的线性天线,回波为入射波在平板上镜面反射的一部分(法向方向反射最大)。

对于UWB雷达,文献[6]中描述了杂波物理模型,但是没有考虑频率的影响。目前采用平板模型对UWB雷达杂波建模的研究很少,虽然文献[2]和[7]中描述了平板模型,但都是基于窄带信号的。在我们的前期工作中[8]研究了宽带雷达杂波平板模型,但该模型比较粗简,未考虑诸多细节因素,比如入射波和反射波的极化、地表电磁特性(相对磁导率、介电常数)、地面凹凸不平和植被覆盖等,对UWB雷达杂波模型的影响。采用平板物理模型和“频率分割子带合成”法对UWB雷达地杂波进行建模和仿真,并且给出了测量区域的杂波统计模型。其基本思路是首先根据地形起伏把测量区域划分成若干个称为平板的小区域;根据窄带满足的条件把UWB划分成一系列子带(即窄带)。其次利用成熟的窄带雷达杂波模型[9-13]建立子带的平板杂波模型。最后,对平板内的分辨单元的各个子带贡献利用如逆傅里叶变换(IFT)的方法进行子带合成,但子带合成不是简单的各个子带的σ0相加,由于彼此间存在一定的相位关系,所以子带合成事实上是矢量合成。以模拟各种UWB雷达杂波的细节部分[7],在子带合成时还进行了细节的补偿。本文目的是通过仿真验证在包含不同的地貌和参数变化在内的条件下的UWB雷达杂波的相关规律,为雷达分析和优化提供参考,而不涉及具体的地貌匹配条件。

2.基本思路及杂波物理建模

2.1 基本思路

在讨论杂波物理建模之前先介绍一下文中的基本思路:首先根据地形变化对杂波测量区域划分成若干个小区域(称为平板),再将UWB雷达信号分割成一系列子带信号,因而利用已有的成熟窄带杂波模型通过子带合成方式获得 UWB雷达杂波模型,文中称之为“频率分割子带合成”法[8]。在每个子带内采用平板物理模型得到低距离分辨率的窄带杂波雷达截面积(RCS),然后通过加权IFT进行子带合成获得UWB雷达杂波的数学模型。对 UWB雷达分辨单元面积归一后获得杂波散射系数(该径向中每个样点即为相应UWB雷达分辨单元的杂波散射系数),带宽越宽,它愈能反映地面散射细节,即地面的一维距离像。最后利用最大似然参数估计(MLE)法估计其统计参数,且利用柯尔莫诺夫-斯米尔诺夫检验(Kolmogorov-Smirnov test)法优选出杂波的统计分布。基本思路见图1流程框图。

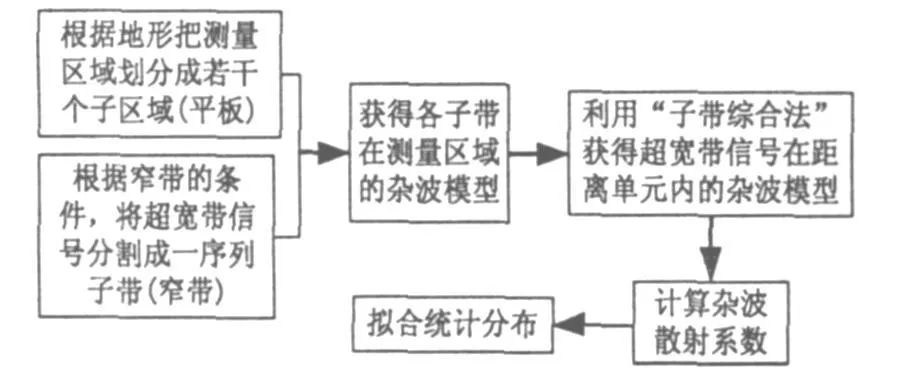
图1 全文基本思路框图

2.2 平板模型

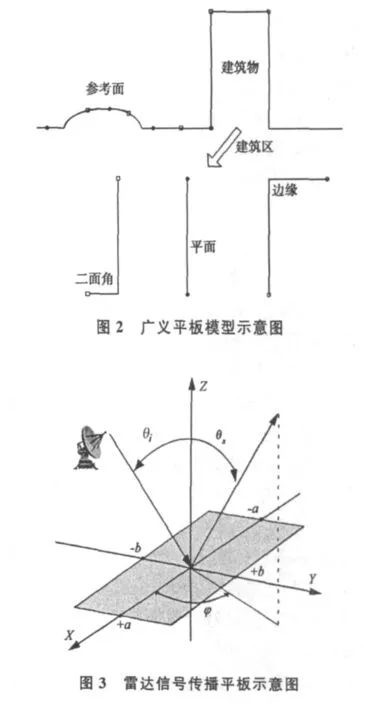
传统的平板模型没有考虑复杂地形,无论地表的形状如何变化,都认为是简单的平板以不同的方向组合而成。对于平原,该模型具有比较好的适应,但对于人工建筑物或树木等,采用传统的平板模型显然不再合适。广义平板模型除了传统的平板模型外,还包括柱面、二面角、边缘和曲面等常见的几何形状。例如,利用柱面模型能较好描述树木,二面角描述建筑物墙面和地面构成的二面关系等。几种常见广义平板模型如图2。

我们在前期工作[8]中通过引入广义平板模型,构建了UWB雷达杂波建模的路线框架,但未考虑诸多细节因素对UWB雷达杂波模型的影响。在此基础上,文中对其中最简单的平板模型进行重点研究,加入一些实际细节因素的影响,且对原杂波模型进行修正,通过仿真预测UWB雷达杂波的一些规律。关于广义平板中其他更复杂的模型的相关研究将在后续工作中开展。传统平板电磁波传播示意图见图 3,其中入射角和反射角分别为θi和θs,且设θi=θs=θ,φ(即式(2)中的 φs)为反射波在 xoy平面上的投影与x轴之间的夹角。窄带雷达杂波反射截面积的数学模型如下[7]

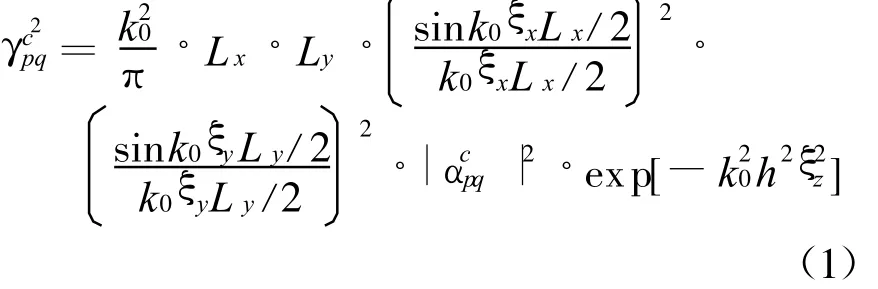
式中:

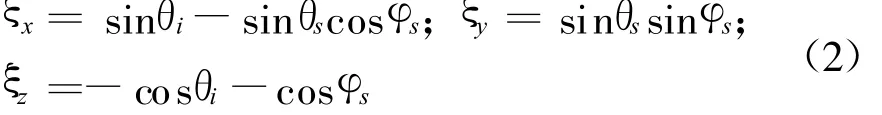
式中,R⊥(θ)为垂直方向上的菲涅耳散射系数

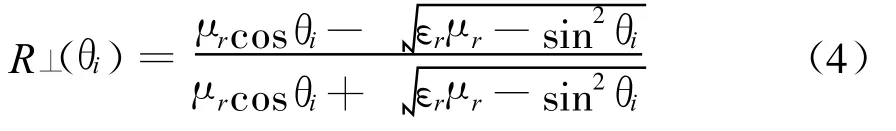
式中,μr和εr分别为地表面的相对磁导率和介电常数。如此可知式(1)不但考虑了地面的起伏,而且考虑了电磁波入射和反射的极性以及地表的电磁特性(介电常数)。通常情况下,起伏的地表上同时考虑植被覆盖更能反映实际地形情况。文中假设植被服从复高斯分布或其它弱拖尾的统计分布(例如杂草、农作物等)。从而子带的杂波平板散射模型[8]为

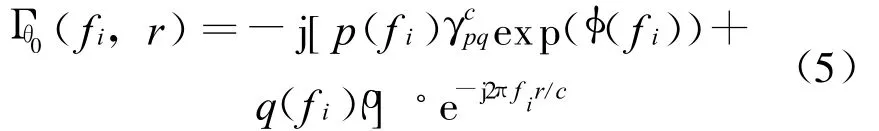
式中:r表示平板上距离门和雷达之间的距离(见式(6));ρ表示植被(例如杂草、农作物等)引起的复高斯或其他弱拖尾的统计值;p(fi)和q(fi)分别为调节高低不平的地面和植被对杂波数据的贡献大小的权值,并且假设式(5)中 γcpq的相位φ(f i)为平板相频特性,假设服从[0,2π]的均匀分布(具体统计分布规律可通过杂波实测数据加以修正)。

式(5)中由于γcpq中相位和ρ都为随机项,所以(,r)也具有统计特性。对于UWB雷达,具有高分辨能力,强散射体贡献未被平均掉,导致杂波统计上表现出长拖尾特性,杂波仿真结果(第3节)证实了这一特征。但是对于测量区域茂密的植被,杂波主要由q(f i)ρ决定。综上可看出,式(5)较文献[8]模型更能反映地形变化以及植被覆盖的一般情况。

2.3 子带合成

一系列子带杂波的贡献通过子带合成的方法实现超宽带雷达杂波建模。设超宽带雷达带宽为BW,从而距离分辨率为δR=c/(2BW)(c为光速)。对位于rk(k=1,2,…),长为L的平板,覆盖的距离门个数M由L/δR取整获得,则M个距离门和雷达之间的距离为

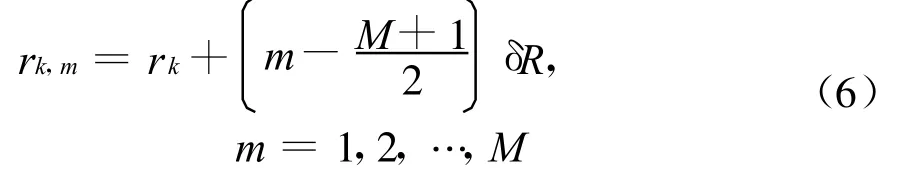
则中心位于r k(k=1,2,…)处的平板的第m个分辨单元的杂波模型(雷达目标截面积)为

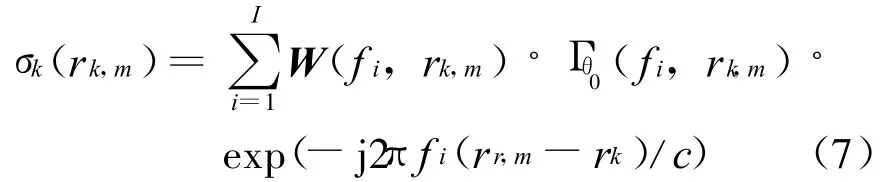
上式事实上是逆傅里叶变换,其中I为子带个数;f i为第i个子窄带的中心频率;rk为平板中心斜距;W(f i,rk,m)为细节补偿因子,实际上反映UWB雷达杂波RCS的频谱结构,该结构受诸多因素(如多径、频率和散射点分布等)的影响,通常是非白的,即频谱的能量可能聚集在较少的几个子带内,即从定性上分析,W(fi,rk,m)在统计上应具有长拖尾特征。文中暂时采用典型的 Lognormal长拖尾分布经过模归一化后进行FFT得到W(fi,rk,m),用以补偿子带合成前子带间杂波细节的光滑化效应[7]。但在实际中具体采用何种长拖尾分布模型,还需进一步地研究,并通过实测数据加以修正。

由式(7)计算σ0[14]为

式中,A为分辨单元的面积。

3.实验及结果分析

仿真条件为:测量区为长15 m、宽1 m的地面;式(6)中r k=5 km;设图 3 中 θi=θs=θ=15°,φ=180°;频率分割的子带相对带宽为1%;入射波和反射波均为水平极化(记为H-H);式(7)中W(f i,r)服从(0,10)的Lognormal分布。

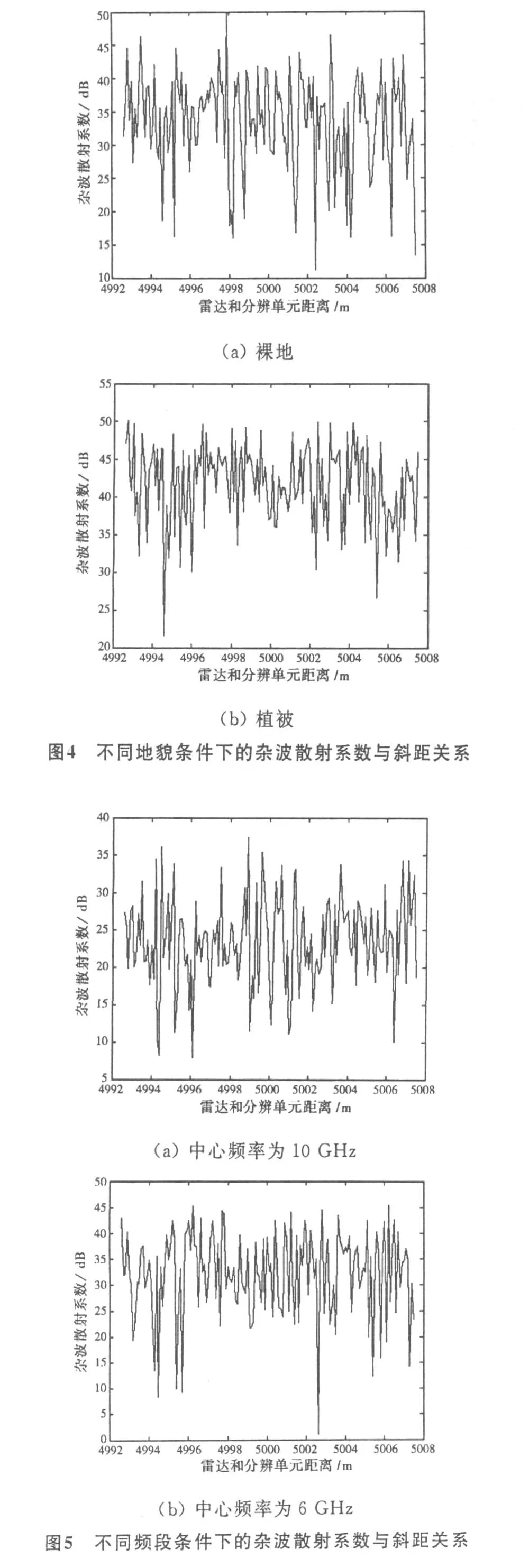
文中UWB信号采用具有代表性的线性调频(LFM)信号,由于篇幅所限,在此未对其他 UWB信号如时域冲击波形(impulse波形)等一一进行讨论。仿真分析的第一种情况是地貌分别为裸地(p(f)=0.8,q(f)=0.1)和植被覆盖(p(f)=0.1,q(f)=0.8)且中心频率为6 GHz,相对带宽为25%(即5.25～6.75 GHz)时的杂波统计特性比较。另一种情况是中心频率分别为6 GHz(5.25～6.75 GHz)和10 GHz(9.25～10.75 GHz),且地貌为裸地(p(f)=0.8,q(f)=0.1)时对杂波统计特性的影响。地貌和中心频率变化时第一组仿真杂波数据分别如图4和图5所示(共进行了15次统计独立重复仿真)

图4给出地貌分别是裸地((a)图)和植被覆盖((b)图)时的杂波散射系数与平板斜距的关系,从图中可以看出在植被条件下杂波和裸地相比起伏要小些,是由于植被的存在,削弱了强散射体的贡献。图5给出了中心频率分别为10 GHz((a)图)和6 GHz((b)图),绝对带宽均为1.5 GHz的杂波散射系数与平板斜距的关系,从图中可知在绝对带宽和测量区域尺寸相同的情况下,中心频率低的杂波散射系数总体要大于中心频率高的,这是因为在绝对带宽相同时,中心频率低,则对应的相对带宽更宽,强散射的反射特性将更加凸显,同时由于低频段平板散射方向图的主瓣更宽,旁瓣更高,所以中心频率低的杂波散射系数大。

利用MLE估计的参数[15]和统计分布拟合情况(柯尔莫诺夫-斯米尔诺夫(K-S)检验统计量D)[16]如表1和表2所示。

表1 不同地貌条件下统计分布参数估计和统计量

表2 不同频段条件下统计分布参数估计和统计量

不同的地貌变化和波段变化时杂波仿真数据直方图及其拟合曲线分别如图6和图7所示(15次统计独立重复仿真)。

从表1看出当地貌为裸地时杂波服从Gen.Gamma分布,而当地貌有植被覆盖时则服从Gamma分布。对于表2,当绝对带宽为1.5 GHz,中心频率为 6 GHz(相对带宽为 25%)时杂波服从Weibull分布,而中心频率为10 GHz(相对带宽为15%)时杂波服从Dagum分布。图6表示其他条件相同,而地貌变化(其上图表示裸地、下图表示植被覆盖)时杂波散射系数的直方图及其统计分布拟合曲线;图7表示其他条件相同,而中心频率变化(其上图表示6 GHz、下图表示10 GHz)时杂波散射系数的直方图及其统计分布拟合曲线。从图6和图7均可发现,杂波散射系数PDF拟合曲线均具有“低重心、重拖尾”的特点。表现出重拖尾是由于UWB具有高距离分辨能力,强散射体可能超过一个或多个距离门,表现出强反射特性,不像窄带信号由于存在大量的弱散射体可能抵消强散射体的贡献,所以对于UWB雷达杂波PDF曲线均具有重拖尾;低重心是指在σ0近0处具有最大的概率,和窄带信号相比,杂波统计分布重心向低散射系数方向移动,其原因是因为高距离分辨率,极强散射体可能遮蔽一定数量的且比其弱的散射体,形成极弱散射或0散射(完全遮蔽),所以PDF曲线重心同时往0散射系数方向移动。由于UWB信号具有高距离分辨,在距离单元中的未被遮蔽的弱散射体数目也很少,表现出重心对应的概率较窄带信号很小。由于杂波的“低重心、长拖尾”的特性,和窄带雷达相比,UWB雷达具有更大的动态范围,从而易造成雷达接收机的饱和甚至过载,导致系统的损坏。同时从图7看出,在绝对带宽相同,而中心频率变小时,由于导致相对带宽的变宽,其统计分布的拖尾比中心频率大的统计分布拖尾更长。

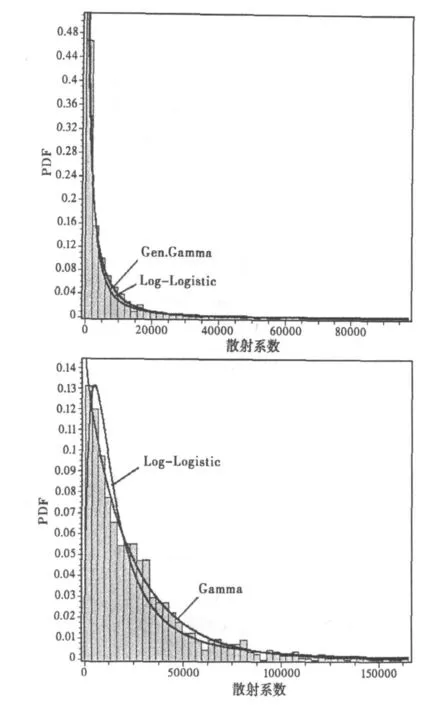
图6 不同地貌条件下杂波统计分布模型拟合

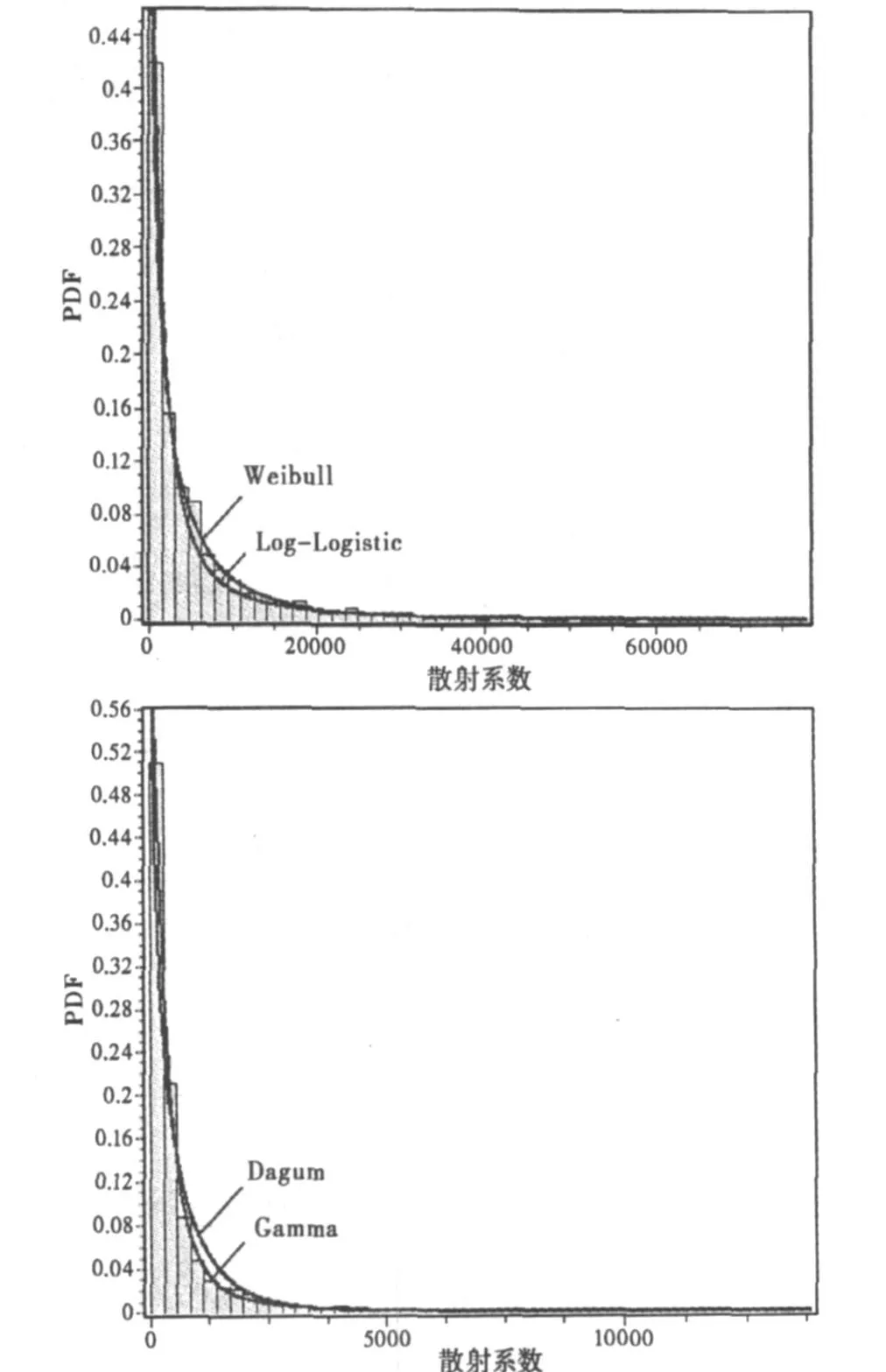
图7 不同频段条件下杂波统计分布模型拟合

通过仿真结果分析进一步发现,在其他条件相同,而地貌变化时,杂波统计分布也随着变化,如图6(上、下图)。根据PDF曲线拟合得知当地貌为裸地时服从Gen.Gamma分布,但当地貌有植被覆盖时,则服从Gamma分布。同样,对于其他条件相同而只有中心频率变化时,杂波统计分布也发生变化,见图7(上、下图),在中心频率为6 GHz时服从Weibull分布,但当中心频率变为10 GHz时则服从Dagum分布。由此发现对于UWB雷达,无法用单一的统计模型对其建模,这和窄带雷达杂波模型(通常地杂波服从具有弱拖尾的Rayleigh分布)具有普适性有很大不同。因此,如果依然对 UWB杂波采用统计建模则带来很大的困难,这也是文中采用物理建模的原因之一。此外,由于传统的目标检测是采用莱曼-皮尔逊(Neyman-Pearson)准则,该准则是基于统计模型的,所以杂波统计模型随参数变化而变化的特性为UWB雷达目标检测带来挑战。

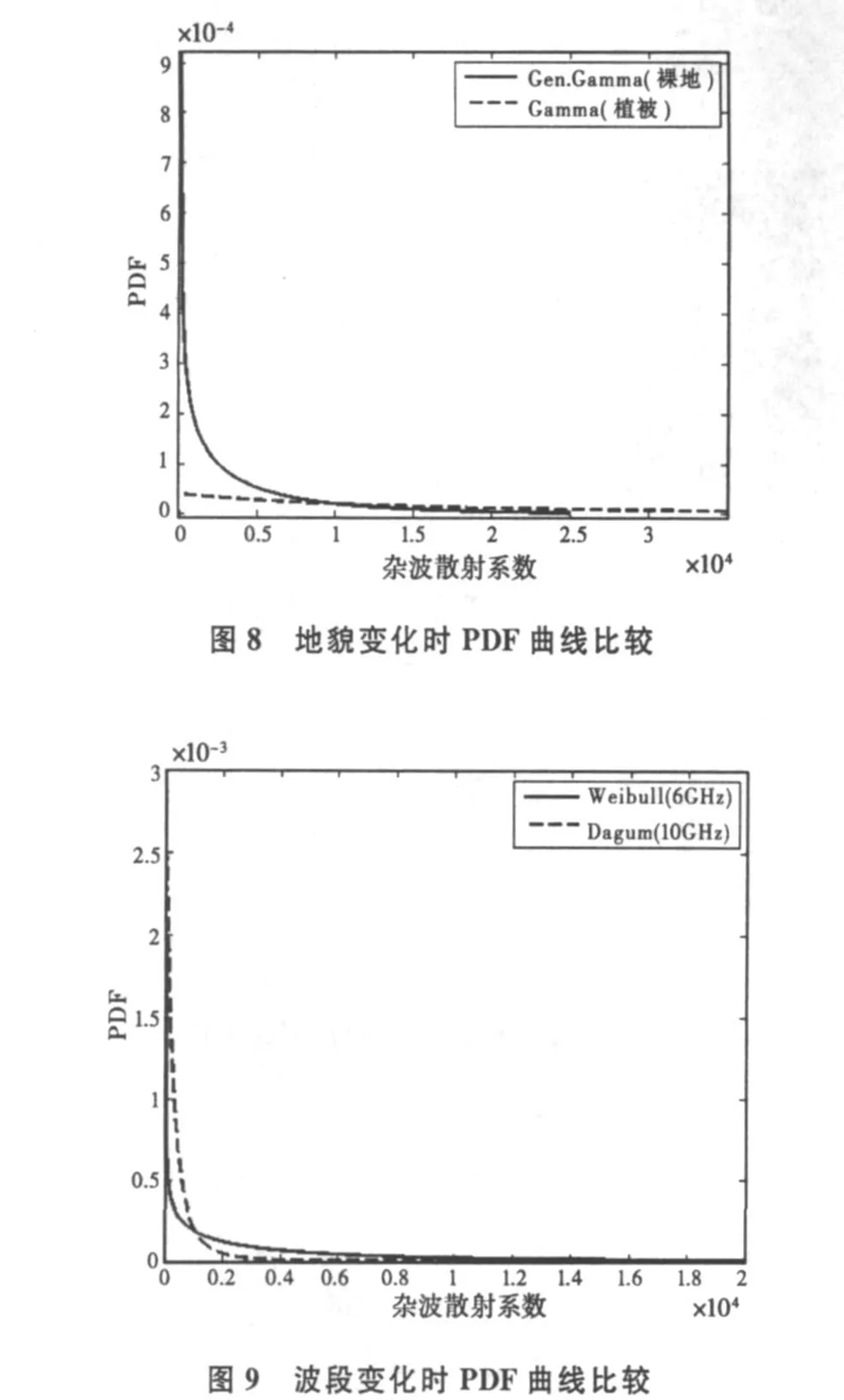
图8和图9分别表示地貌和波段的变化时统计分布曲线比较。图8是地貌分别为裸地和植被时PDF曲线局部放大图(由于植被条件下拖尾比裸地的要长得多,局部放大以便更清楚看出两者PDF曲线的关系),根据计算得出拟合曲线在联合概率密度函数CDF值为0.9处对应的散射系数为1.3408×104(裸地)和5.6899×104(植被)。图9是中心频率分别为6 GHz和 10 GHz的 PDF曲线,在CDF值为0.9时,计算出散射系数分别1.259×104(6 GHz)和1.3618×103(10 GHz)。由图9可知当相同的绝对带宽但中心频率变化时,相同CDF值对应的散射系数位置也发生移动,对于较小的中心频率,当CDF值为0.9时对应的杂波散射系数位置更远离0散射系数的位置,这是由于较小的中心频率在相同的绝对带宽条件下有较大的相对带宽,从而具有更长的拖尾,且PDF曲线重心沿PDF轴下移所致。但由此会导致虚警概率增大,为雷达目标检测、辨识和数据处理带来困难,更有可能在强散射体占优的分辨单元内由于很小的信杂比(SCR)而导致目标被“埋没”,造成距离盲区。

4.结 论

文中采用物理平板模型和“频率分割子带合成”法对UWB雷达杂波进行建模与仿真。首先根据地形把地面划成若干个小区域,同时把超宽带分割成一系列子带;然后分别计算子带的杂波贡献;最后利用子带合成得到超宽带雷达杂波的模型。通过统计模型建模只能适应具体地形、季节和某时间的杂波情况;文中构建的UWB雷达杂波模型不但反映了地面凹凸不平,植被覆盖的现象,而且考虑了地表面的电磁特性(如介电常数)和电磁波入射与反射的极化特性,具有高保真性。仿真结果表明:对于UWB雷达杂波,在其他条件相同的情况下,地貌或者波段(或中心频率)的变化,杂波的统计分布也跟随变化,因此,对于UWB雷达杂波不能用固定的统计分布对其建模,同时由于长拖尾的杂波容易导致虚警概率增大,这给UWB雷达目标检测带来挑战;UWB雷达杂波均具有长拖尾的统计分布特征,在接近0散射系数σ0处概率密度最大,即“低重心,长拖尾”。且随着相对带宽的增大,拖尾加重,则UWB雷达具有更大的动态范围,从而容易出现接收机的饱和甚至过载现象。经仿真分析可知:仿真结果与UWB雷达杂波定性分析的规律基本符合。后续工作中将进一步研究针对其他UWB信号(如时域impulse波形等)的杂波建模和仿真。

[1] JAMES D.Taylor.Introduction to ultra-wideband radar system[M].CRC Press,Inc.,1995:1-2.

[2] SKOLNIK M I.Radar handbook[M].3nd ed.McGraw-Hill,Inc.,2008:14.

[3] ANASTASSOPOULOS V,LAMPROPOULOS G A,DROSOPOULOS A,et al.High resolution radar clutter statistics[J].IEEE Trans on AES,1999,35(1):43-60.

[4] GRECO M S,GINI F.Statistical analysis of high-resolution SAR ground clutter data[J].IEEE Trans on GRS,2007,45(3):556-575.

[5] GARCIA-FERNANDEZ A F,GRAJAL J,YESTEOJEDA O A.Analysis of ISAR images of a helicopter by a facet model[C]//IEEE International Conference on Radar.USA,2008:32-37.

[6] JACHSON JA,MOSES R L.Clutter model for VHF SA R imagery[J].Proceedings of the SPIE,2004,5427.271-282.

[7] RUCK G T,BARRICK D E,STUART W D,et al.Radar Cross Section Handbook Volume 2[M].New York:Plenum Press,1970:700-702.

[8] XU Zhiyong.Subband Systhesis mehtod for simulation of wideband radar clutter[C]//IET International Radar Conference.Guilin,China,April,2009:20-22.

[9] BILLINGSLEY B,FARINA A,GINI F,et al.Statistical analysis of measureed radar ground clutter data[J].IEEE Trans on AES,1999 35(2):579-592.

[10] MA Xiaoyan,FANG Xueli,CHEN Song.Radar clutter recognition based on feature extraction byαtruncation set[C]//Proc.IEEE,IRC'.Beijing,China,2001:436-439.

[11] BILLINGSLEY J B.Low angle radar land clutter:measurements and empirical models[M].USA,William Andrew Publishing,Inc.,2001:143-242.

[12] 张长隆,王 展,周良柱.线性调频脉冲压缩雷达杂波统计模型分析[J].电波科学学报,2004,19(2):240-244.

ZHANG Changlong,WANG Zhan,ZOU Liangzhu.Clutter statistical analysis for linear f requency modulated pulse compression radar[J].Chinese Journal of Radio Science,2004,19(2):240-244.(in Chinese)

[13] 杨 博,周一宇,黄知涛.空基运动平台照射源的无源雷达杂波建模[J].电波科学学报,2009,24(6):1099-1103.

YANG Bo,ZHOU Yiyu,HUANG Zhitao.Modeling of the ground clutter on passive radar based on airborn illuminator[J].Chinese Journal of Radio Science,2009,24(6):1099-1103.(in Chinese)

[14] SKOLNIK M I.Introduction to Radar Systems(3rd edition)[M].Beijing,China,Publishing House of E-lectronics Industry,2006:403-404.

[15] LIANG Jing,LIANG Qilian,SAMN S W.Foliage clutter modeling using the UWB radar[C]//IEEE International Conference on Communications.Beijing,China,19-23 M ay 2008:1937-1941.

[16] STEPHENS M A.EDF Statistics for goodness of fit and some comparisons[J].Journal of the American Statistical Association 69,1974:730-737.