MIMO-OFDM快衰落信道的压缩感知估计方法

周小平 方 勇,2 汪 敏

(1.上海大学通信与信息工程学院,特种光纤与光接入网重点实验室,上海 200072;2.新型显示技术与应用集成教育部重点实验室,上海 200072)

1.引 言

正交频分复用(OFDM)具有高速的数据传输能力、高效的频谱利用率和抗多径干扰能力,因而在无线通信领域引起了广泛关注。为了进一步提高系统容量,将OFDM 与多输入多输出(MIMO)相结合实现多天线分集[1-2]。但是,在快衰落环境中,MIMOOFDM系统容量常常与理想状况相差甚远。为获得较好的系统性能,一般都要求收发端有效地完成信道估计。

传统导频辅助的信道估计方法[3-6],首先估计导频子载波点上的频域冲击响应,然后通过插值的方法得到对应数据子载波上的频域冲击响应。采用这种方法,导频的插入比例需要满足奈奎斯特采样频率条件,也即受信道衰落程度的影响。然而该条件是建立在无线信道传播于丰富地散射环境的基础上,并没有考虑快衰落MIMO-OFDM信道具有可稀疏性。

最近Cand'es和 Donoho提出一种新颖的理论—压缩感知(Compressed Sensing,CS)[7-8],该理论与传统的奈奎斯特采样定理不同,它指出,只要信号在某个变换域具有可稀疏性,那么信号的投影测量数据量将远远小于传统采样方法所获的数据量,并且可从这些少量的测量数据中以高概率重构出原信号。对于单输入单输出(SISO)OFDM系统,文献[9-10]把感知理论应用于慢衰落信道估计中,为提高系统频谱利用率提供了一个方向。而对于MIMO-OFDM系统,文献[11]提出了基于导频辅助的慢衰落信道估计方法。然而在快衰落环境下,由于上述信道估计算法只考虑了时延域信道的稀疏性,并没有考虑空间域和多普勒域信道的稀疏性,所以在空间和频率的测量位置与实际信道变化的范围存在偏差,容易引起功率混叠与泄漏,致使信道稀疏性不强,性能不好。同时在进行信道测量时,使用了计算量大的信道测量矩阵。因此,推导稀疏性更强、频谱利用率高、计算复杂度低和估计性能好的MIMOOFDM系统快衰落信道估计方法就显得十分必要,该文将解决这个问题。

该文所提出的MIMO-OFDM系统快衰落信道估计方法,其主要包括三个方面研究:在角时延多普勒域快衰落MIMO-OFDM信道的稀疏表示;通过一种少量导频结构随机测量矩阵在角时延多普勒域对信道进行测量;最后以高概率重构出快衰落信道。

2.系统模型

考虑一个有 Nt根发送天线,Nr根接收天线和K个子载波的MIMO-OFDM系统,其基本模型如图1所示。

图1 MIMO-OFDM系统模型

假设n时刻第t根发射天线发送的OFDM符号用K×1向量 Xt(n)表示。发送之前该向量经过IDFT处理。为了有效对抗多径时延扩展,还需要在OFDM符号间加入循环前缀(CP)作为保护间隔,循环前缀需要大于信道冲击响应的最大抽头数。接收端去除循环前缀后,接收天线r上的信号可表示为

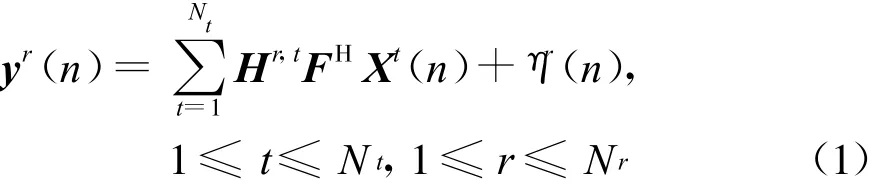
式中,假如在慢衰落信道环境下,Hr,t为一个循环矩阵[1],其第一列为 [hr,tT,01×(K-L)]T,其中符号(·)T表示矩阵转置,并且大小为L×1的向量,hr,t用来表示从第t根发射天线到第r根接收天线之间长度为L的信道冲激响应。F表示功率归一化的K点DFT矩阵。将Hr,t进行特征值分解,容易得到Hr,t。进一步可以推得

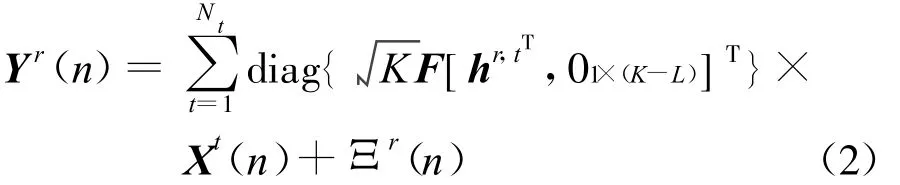
式中,Ξr(n)为均值为零方差为σ2n的加性高斯白噪声ηr(n)的傅立叶变换。然而在移动台高速运行的时候,快速移动在频域上产生多普勒效应而引起频率扩散,多普勒效应引起了时间选择性衰落;同时,在不同的地点、不同的传输路径衰落特性不一样,多径效应引起了空间选择性衰落。即,在多径效应和多普勒效应引起的快衰落环境下,由于此时所有的信道抽头是随时间而快速变化的,所以KL(Q+1)×1维信道函数Hr,t将不在是一个循环矩阵,其中,Q为信道多普勒扩展阶数,L为从第t根发送天线到第r根接收天线的最大抽头数。若使用传统最优信道估计方法,则所需最少导频数为KL(Q+1)。因此,为提高数据传输效率,该文推导了基于压缩感知的MIMO-OFDM系统快衰落信道估计方法。

3.压缩感知信道估计

3.1 MIMO-OFDM信道稀疏变换

为了能在压缩感知理论框架下研究MIMOOFDM系统信道估计,需要对式(2)中 MIMOOFDM无线信道进行稀疏变换。文献[9-11]在时延域研究了慢衰落信道的稀疏性,而在快衰落环境下,需要同时考虑空间域、时间域和多普勒域信道的稀疏性,目的是使在空间、时间和频率的测量位置与实际信道变化的范围相符合,减少了功率混叠与泄漏,提高信道的稀疏性。信道稀疏性越强,性能改善越好。首先考虑信道在空间域的稀疏性,结合文献[12-13],一个发送天线和一个接收天线形成一个角域区域,而每个角域区域内的信道系数是有限的,因此,可在角域考虑信道冲激响应的稀疏特性,将发送信号和接收信号进行角域正交变换:

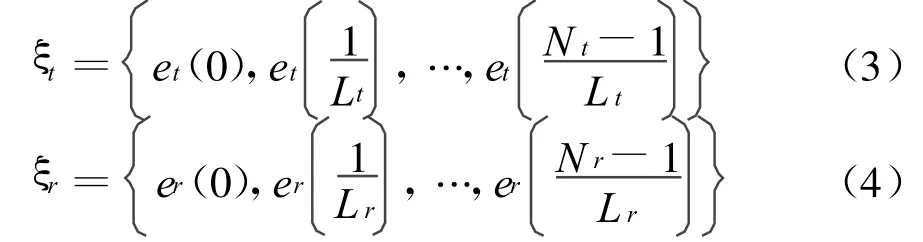
式中:Lt=NtΔt和L r=NrΔr,分别表示发送天线和接收天线均匀线阵的归一化长度和分别为发射单位空间特征图和接收单位空间特征图。让at和ar是整体天线矩阵,其列向量分别是式(3)和式(4)。这样,便根据角域正交变换得到了信道冲激响应角域稀疏向量Hr,t(n)a r aHt。而Hr,t(n)在高速无线OFDM系统的时延多普勒域同样具有稀疏的特性。设Hr,t(n,k)第t发送天线和第r接收天线在n时刻第k子载波的多径信道频率冲激响,可表示为

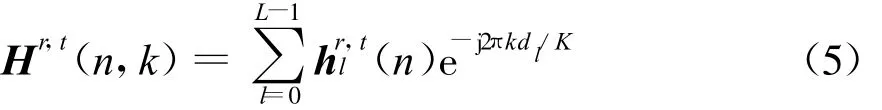
并且第l条径可表示为

定义hr,tl(n)=[hq,rl(n,0),…,hq,rl(n,K-1)],这样hr,tl(n)可表示为

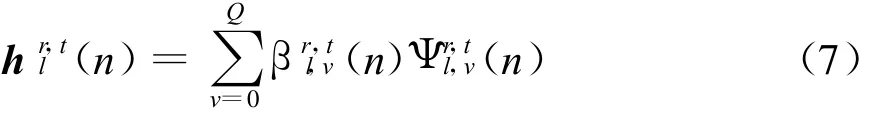
式中 , Ψr,tl,v(n)=[e-j2π(v-Q/2)GK,…,e-j2π(v-Q/2)(K-1)/GK] 。第i个时刻第L条路径信道脉冲响应可以表示为T,则hr,t(n)可表示为

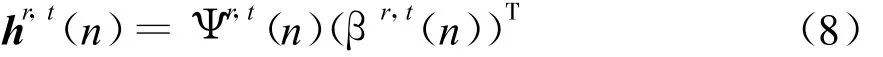
同时

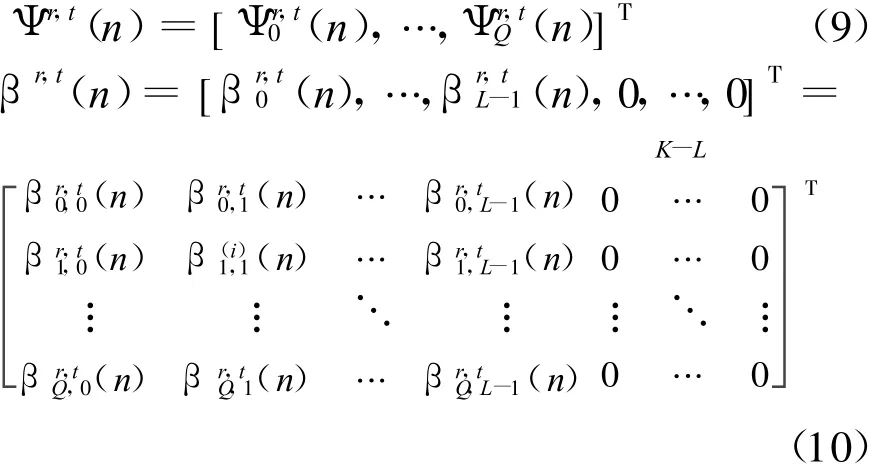
现在,把hr,t(n)信道估计问题转化为估计βr,t(n)的问题,βr,t(n)的功率为

式中:符号(·)H表示矩阵的Hermitian;E[βr,t(n)2]转化为 δr,t(n)=[E βr0,t(n)2,…,E βrL,-t1(n)2];βr,t(n)非零能量表示为.因此,假如=S ＜ Nt Nr KL(Q+1),那么快衰落信道就是稀疏的,其稀疏度为S,其中‖·‖ℓ0计算向量的非零数。因此,在角时延多普勒域可将 NtNrKL(Q+1)维MIMO-OFDM信道变换为S维稀疏矩阵h(n)=[(I Nt⊗aHr)(aTt ⊗INr)]Ψ(n)(β(n))T,其中[(I Nt⊗ aHr)(aTt⊗I Nr)]是 Nt N r⊗Nt N r维角域矩阵,Ψ(n)时延多普勒域矩阵,β(n)是需要估计的稀疏信道冲激响应系数。这样,Nt N r KL(Q+1)维信道h(n)转化为S稀疏信道冲激响应系数β(n),而S远小于N tN rKL(Q+1).

3.2 随机导频测量矩阵设计

通过上一节分析,可将无线信道冲激响应h(n)在角时延多普勒域 A(n)进行稀疏变换 h(n)=A(n)β(n),得到稀疏系数为β(n)。要想能准确地重构此稀疏系数,Candˋes和Tao给出并证明了传感矩阵必须满足受限等距特性(RIP)[7,14]。若令 Φ为M×Nt N r KL(Q+1)(M＜＜Nt N r KL(Q+1))维传感矩阵,则可得该传感矩阵的 T列子矩阵为 M ×T维ΦT。那么对于任意S稀疏信号(其S个非零值的位置是未知的)h(n),能够从Y(n)=ΦA(n)β(n)精确重构出β(n)的充分条件是传感矩阵 Φ对于S稀疏信号h(n)和常数δS∈(0,1)有S阶约束等距性,即

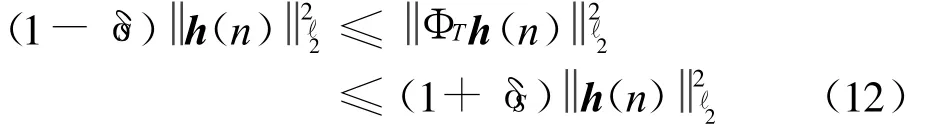
式中:· ℓ2表示ℓ2范数;对所有子集T满足T ≤S,S稀疏向量h(n)∈RT.

为了使传感矩阵 Φ满足受限等距特性RIP,需要从导频输入输出关系着手研究。文献[9]给出了Toeplitz测量矩阵,然而该测量矩阵具有较高的计算复杂度,在接收端存在大规模矩阵求逆运算,其复杂度随着天线数和子载波的增加呈指数倍增加,同时对导频的输入输出也比较困难,而且只能局限于时域信号处理。为了减少计算复杂度,同时又可在角时延多普勒域进行稀疏系数重构,该文给出一种满足约束等距性条件RIP随机结构导频测量矩阵。设此随机结构导频测量矩阵为三个矩阵的乘积,即D(n)R(n)～F,其中,～F为由 K倍标准DFT矩阵对应的M行和前L列组成的矩阵。

R(n):为 Nt根发送天线随机导频发生矩阵R(n)=[R1(n),…,RNt(n)]T,当第n时刻随机性导频发生器随机选择第t根天线用于发送导频,而该天线再随机选择Mt(n)个子载波{k 1,…,kMt(n)}用于承载导频数据+1或-1(等概率分布),其余K-Mt(n)个子载波用于承载用户数据,则可用Rt(n)表示第n时刻第t根天线随机性导频发生矩阵,而Rt(n)为 K×K维对角矩阵,即Rt(n)=diag{Rt(n,0),…,Rt(n,K-1)}.第n时刻所有发送导频数为需要满足 S阶 RIP:M≥CS log(Nt N r KL(Q+1)/S),那么重构稀疏系数β(n)的概率为1-e-CM,其中C≥1为过采样因子[7]。

D(n):为 Nt根发送天线下采样矩阵D(n)=[D1(n),…,DNt(n)]T,矩阵D(n)的取值是根据矩阵Rt(n)来决定的,令Dt(n)为K×K维对角矩阵,当Rt(n)用于发送导频,则Dt(n)根据导频子载波位置{k1,…,kMt(n)}在对角矩阵相应位置放数据其余的数据0。那么Dt(n)取值的概率为

3.3 稀疏信道重构

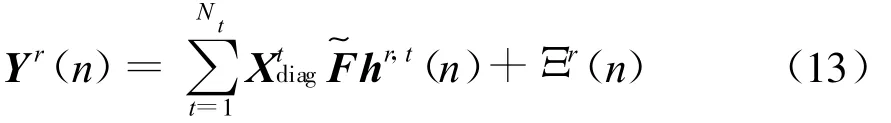
将式(8)和角域矩阵代入式(13),可推导

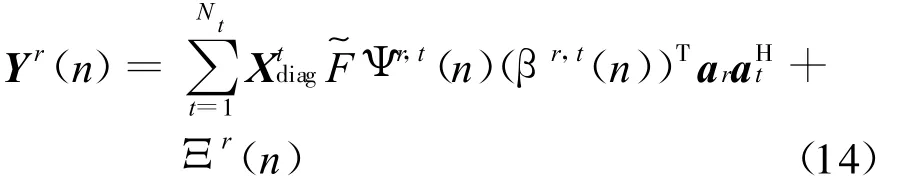
进一步,根据3.2小节导频发生矩阵Rt(n),可以得到n时刻各发射天线与第r个接收天线之间上的接收信号

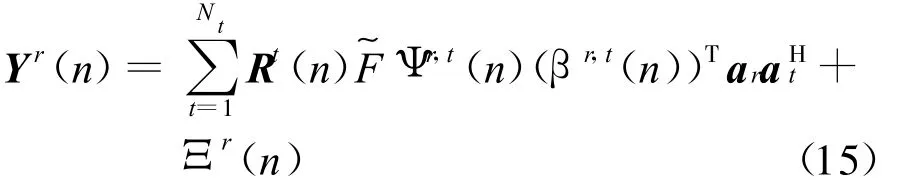
再利用下采样矩阵D(n)对接收信号进行下采样,可以得到n时刻各发射天线与第r根接收天线之间导频点上的接收信号Yrp(n),可表示为

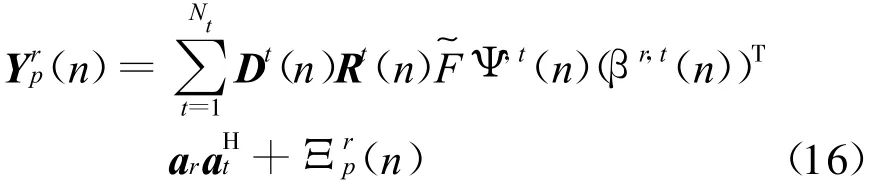
式中:Ξrp(n)为Dr(n)Ξr(n)。将式(16)表示成矩阵形式

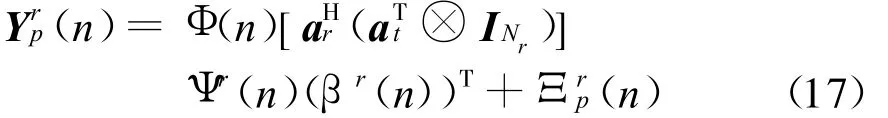
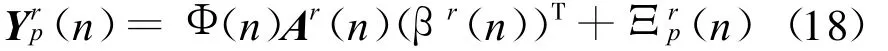
进一步可得到n时刻N t根发射天线与N r第r根接收天线之间导频点上的接收信号Nr×N t维接收信号(n)=[Y1P(n),…r(n)]T,可表示为

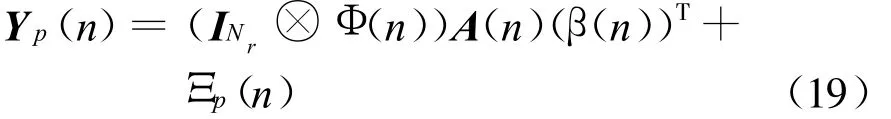
式中:A(n)=[(I Nt⊗)(⊗I Nr)]Ψ(n)为Nt N r KL(Q+1)×Nt N r KL(Q+1)维角时延多普勒域矩阵 ;β(n)=[β1(n),…,βNr(n)] 为 S 稀疏信道冲激响应系数;Φ=INr⊗ Φ(n)为 M ×Nr N tKL(Q+1)导频测量矩阵。

利用Dantzig Selector[15]重构S稀疏信道冲激响应系数β(n)。令 δ2S＜-1,对于任何b ≥0,可使得λ=(2σ2(1+b)log(NrNtKL(Q+1)))1/2,则估计(n)的方程为

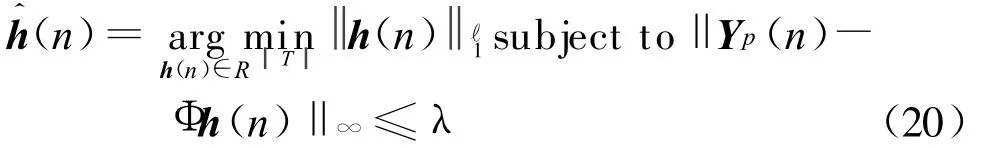
式中,·∞表示ℓ∞范数,估计^h(n)满足式中,

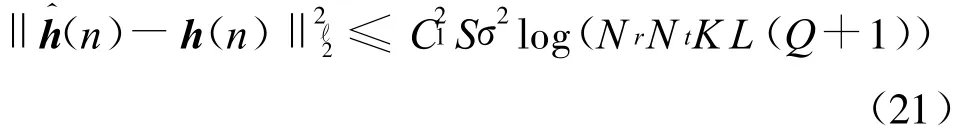
3.4 性能分析

对结构随机导频矩阵的 RIP进行分析。由式(15),可得第t根发射天线和第r根接收天线接收信号

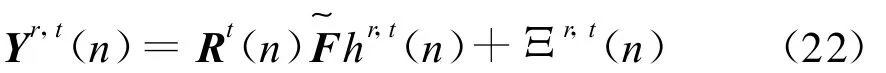
由于Rt(n)具有正交归一性,有

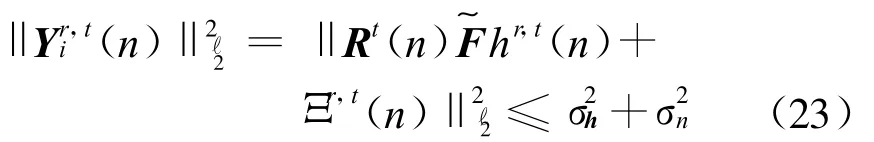
σ2h为信道功率,而由式(16),可得

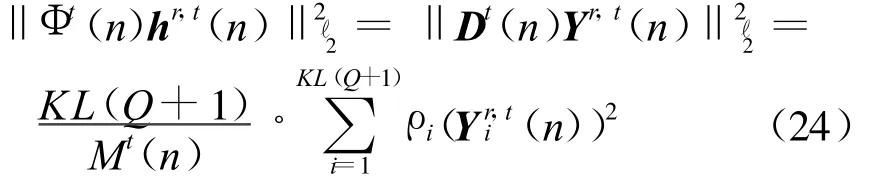
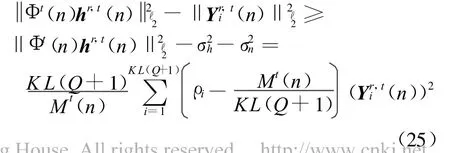
式(25)右边等于零均值独立随机变量的和,即E{‖Φt(n)hr,t(n)‖2ℓ2-σ2h-σ2n}=0,方差为

再利用伯思斯坦不等式[16],概率为

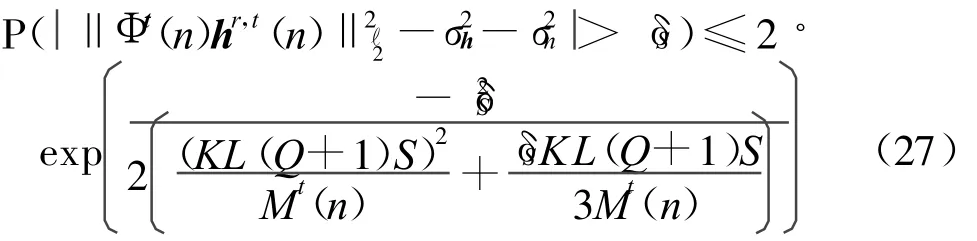
然后,分析系统计算复杂度。与传统导频辅助的信道估计方法[3-6]不同的是:该方法并不需要先估计导频子载波点上的频域冲击响应,然后通过复杂的插值方法得到对应数据子载波上的频域冲击响应,而是先通过少量的导频测量信号估计出少量的非零信道系数(n),然后把得到的少量非零信道系数(n)与角时延多普勒域A(n)=[(INt⊗aHr)(⊗I Nr)]Ψ(n)相乘就可以得到所有子载波上的频域冲击响应,因此,大大减少了计算复杂度。

最后,分析系统的传输效率。让SD={(v,l,ar,at):β(v,l,ar,at)＞0}为信道冲激响应非零系数集合,若S=SD≪NrNtKL(Q+1),对于该文所采用方法,只要导频满足M ≥CS log(Nt Nr KL(Q+1)/S),就可以准确重构s稀疏信道冲激响应系数β(n)。而传统方法基于均方误差最小的准则,推导了最优导频序列数为Nr NtKL(Q+1)。由此可见,该文所采用方法能提高数据传输效率。

4.实验结果分析

这一节给出了一些仿真结果来证实该文所提出算法的有效性与理论分析的正确性。分别考虑了收发天线皆为2和收发天线皆为4的MIMO-OFDM无线通信系统,载波频率5 GHz,基带采样频率5 MHz,子载波个数为1028,采用的调制方式为16-QAM(正交幅度调制)。采样间隔 Ts为204.8μs。

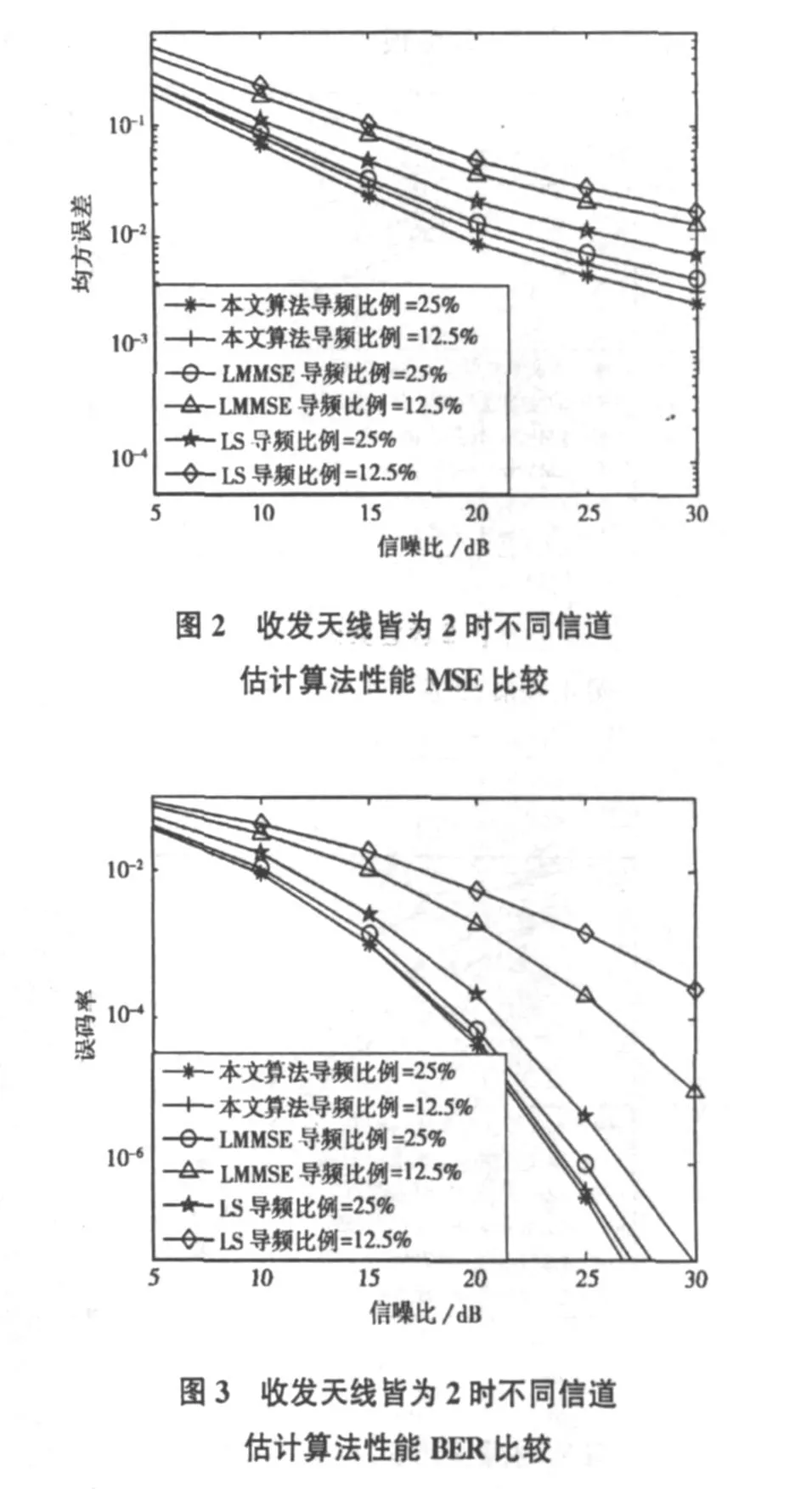
图2,3比较了各信道估计算法在不同信噪比下的MSE和BER性能比较分析曲线。考虑收发天线皆为2,且信道抽头数L=15,当移动台的最大速率取150 km/hr时,最大多普勒频移为506.25 Hz。从图中可以明显看出,在导频数量分别为所有传输符号数量的25%和12.5%时,LS和LMMSE算法MSE性能随着导频的减少下降很快,但该文所采用算法性能变化不大。原因是在导频数量为所有传输符号数量的25%时,最优导频序列数满足传统方法的均方误差最小准则;而在导频数量为所有传输符号数量的12.5%时,这个准则就无法成立,信道估计误差呈急剧下降趋势。该文所采用算法却不受这个准则限制,因此,性能变化不大。表明了压缩感知理论用于快衰落信道估计可以减少导频数量,提高数据传输效率。

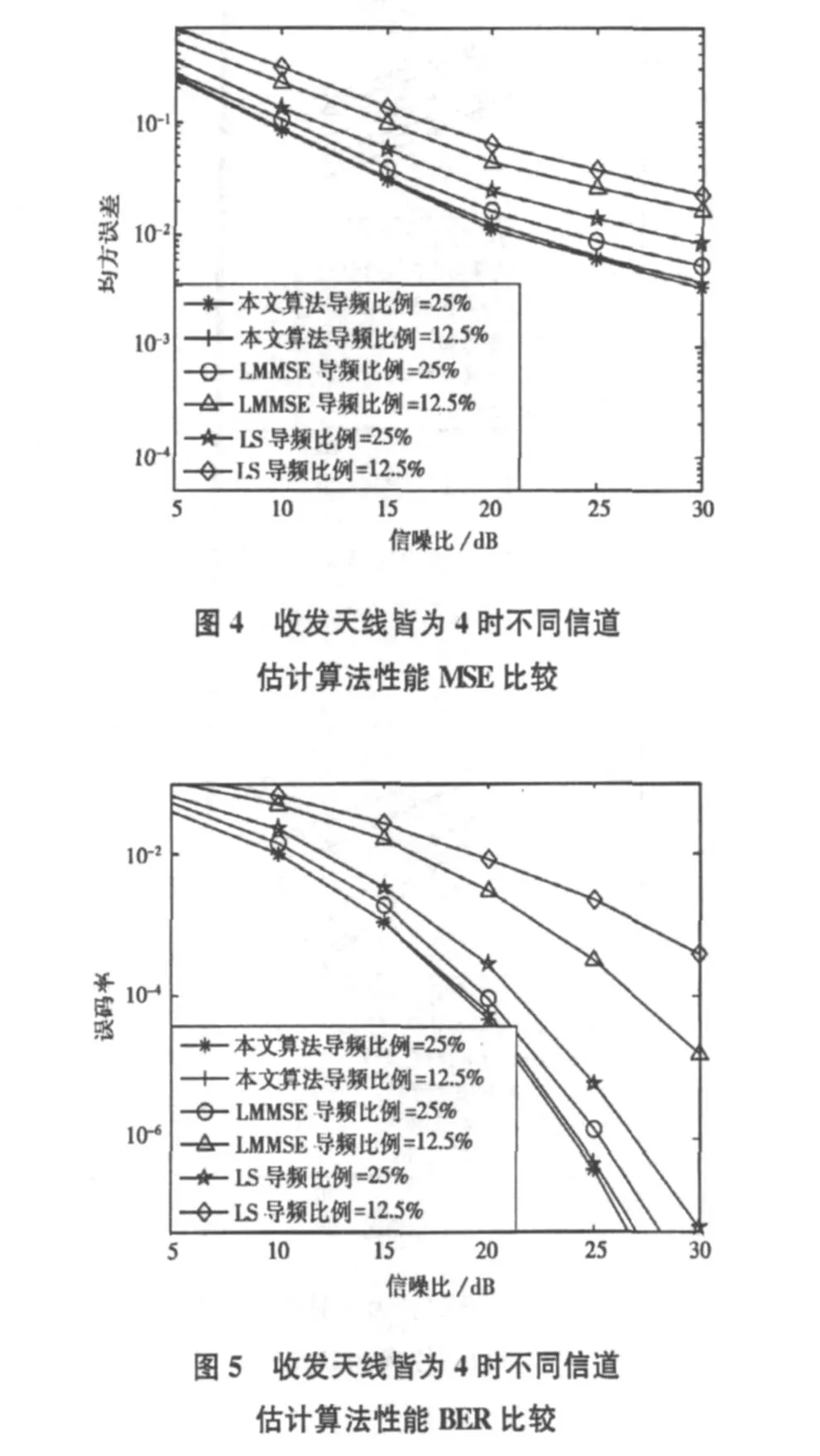
同样,图4,5比较了各信道估计算法在不同信噪比下的MSE和BER性能比较分析曲线。但这时考虑收发天线皆为4,且信道抽头数L=20,当移动台的最大速率取200 km/hr时,最大多普勒频移为675 Hz。从图2～5分析曲线可以明显看出,快衰落信道对传统信道估计算法有一定的影响,而对该文利用了快衰落MIMO-OFDM信道在角时延多普勒域的强稀疏性,所以影响很小。

5.结 论

针对快衰落MIMO-OFDM系统中导频过多导致的低数据传输效率,估计性能差以及计算复杂度高的弊端,提出了基于压缩感知理论的 MIMOOFDM系统快衰落信道估计算法。该算法同时考虑空间域、时间域和多普勒域信道的稀疏性,减少了功率混叠与泄漏,提高信道的稀疏性。基于压缩感知的RIP准则,推导了一种少量导频随机结构测量矩阵,用于测量快衰落信道在角时延多普勒域稀疏系数。该算法降低了系统对导频的需求,提高了系统的数据传输效率;减少了计算复杂度,提高了估计性能。

[1] BARHUMI I,LEUS G,and MOONEN M.Optimal training design for MIMO OFDM systems in mobile wireless channels[J].IEEE Transactions on Signal Processing,2003,51(6):1615-1624.

[2] MAAREF A,AISSA S.Impact of spatial fading correlation and keyhole on the capacity of MIMO systems with transmitter and receiver CSI[J].IEEE Transactions on Wireless Communications,2008,7(8):3218-3229.

[3] SONG WONGYU,LIM JONGTAE.Channel estimation and signal detection for MIMO-OFDM with time varying channels[J].IEEE Communications Letters,2006,10(7):540-542.

[4] JACOBSL,MOENECLAEY M.Effect of MMSE channel estimation on BER performance of orthogonal space-time block codes in rayleigh fading channels[J].IEEE Transactions on Communications,2009,57(5):1242-1245.

[5] DANIEL N L,MICHAEL P F.Urbashi M.On Channel estimation in fast fading mobile coded MIMO OFDM[C]∥IEEE International Symposium on Information Theory,2009:754-758.

[6] 王 晗,汪晋宽.MIMO-OFDM系统信道估计中的最优导频设计[J].电波科学学报,2008,23(3):501-505.

WANG Hang,WANG Jinkuang.Optimal pilot tone design in MIMO-OFDM systems[J].Chinese Journal of Radio Science,2008,23(3):501-505.(in Chinese)

[7] CAND ES E J,ROMBERG J,TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete f requency information[J].IEEE Trans Information Theory,2006,52(2):489-509.

[8] Donoho D L.Compressed sensing[J].IEEE Trans Information Theory,2006,52(4):1289-1306.

[9] SHARPM,SCAGLIONE A.Application of sparse signal recovery to pilot-assisted channel estimation[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing,2008:3469-3472.

[10] BAJWA W U,HA UPT J,GIL R,et al.Compressed channel sensing[C]∥42nd Annual Conference on Information Sciences and Systems,2008:5-10.

[11] KHOJASTEPOUR M A,GOMADAM K,WANG XIAODONG.Pilot-assisted channel estimation for MIMO OFDM systems using theory of sparse signal recovery[C]∥IEEE International Conference on A-coustics,Speech and Signal Processing,2009:2693-2696.

[12] LI HUANG,CHIN KEONG HO,BERGMANS J W M,et al.Pilot-aided angle-domain channel estimation techniques for MIMO-OFDM systems[J].IEEE Transactions on Vehicular Technology,2008,57(2):906-920.

[13] 许 鹏,汪晋宽,祁 峰.基于奇异值分解的MIMO-OFDM系统角域MAP信道估计算法[J].电波科学学报,2009,24(5):854-859.

XU PENG,WANG Jinkuang,QIFeng.Angle-domain M AP channel estimation algorithm by singular value decomposition for MIMO-OFDM systems[J].Chinese Journal of Radio Science,2009,24(5):854-859.(in Chinese)

[14] BARANIUK R.Compressive sensing[J].IEEE Signal Processing Magazine,2007,24(4):118-121.

[15] CAND'ES E J,TAO T.The dantzig selector:Statistical estimation when p is much larger than n[J].Ann.Statist.,2007,35(6):2313-2351.

[16] FRAPPIER C,Note on bernstein's inequality for the third derivative of a polynomial[J].Journal of Inequalities in Pure and Applied M athematics,2004,5(1):1443-5756.