矩形钢管混凝土拱模型试验
朱 斌 刘祖华
0 引言
钢管混凝土结构中,在轴向力的作用下混凝土的变形受到钢管的约束处于三向受力状态,混凝土的承载力会显著提高。同时,钢管的套箍作用能大大提高混凝土的塑性。另外,钢管内填混凝土能提高钢管壁的稳定性,使结构整体稳定性得到提高。此外钢管可作为混凝土浇筑模板,为施工提供便捷。因此,在拱形建筑物中采用钢管混凝土结构具有很大优越性。
某建筑在使用阶段外表面需承受0.8倍标准大气压的作用,因此设计采用圆弧形拱屋架结构。该结构体系主受力构件为矩形钢管混凝土拱,每个拱上有26个纵向次梁,次梁上安置抵抗大气压的弧面板。
拱截面尺寸为:方钢管混凝土构件,尺寸1 000 mm×2 000 mm,钢管壁厚38 mm,内填C50混凝土。钢管内壁设置栓钉。拱身半径 R=30.74 m,跨度 L=59.244 m,拱高 H=22.525 m。拱肋下端采用埋入式拱脚,拱脚与基础刚接。设计单位根据等效梁柱法初步确定了拱的截面尺寸,但还需要进行模型试验以确定拱肋的承载力。
1 试验方法
1.1 模型设计
根据设计单位提供的图纸,综合考虑模型的相似关系、尺寸效应、试验场地、加载条件以及材料限制等因素的影响,采用1/9.5的缩尺比例制作拱的模型试件。
本试验中所用材料按原型结构设计采用,钢管用Q345热轧薄钢板,混凝土用C50无收缩混凝土,采用海螺P.O42.5水泥,细石骨料,掺膨胀剂使混凝土微膨胀无收缩,水灰比为0.32。
根据相似关系要求,确定拱试件的几何尺寸见表1。

表1 拱试件尺寸
1.2 加载方法
该建筑在使用时,围护体系将承受0.8个大气压的压力,即相当于80 kN/m2的面荷载。面荷载的作用方向为垂直指向外壳表面(耐压钢板),通过次梁,这些面荷载合成一个指向拱轴线圆心的集中力,每根次梁处为一个集中力。按照设计要求,共计有26根次梁,它们间距相等,所以这些集中力大小相等。
由以上的相似关系可以得到拱试件的试验加载。
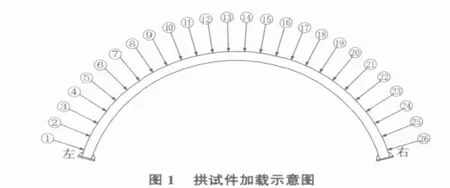
试验加载采用一个千斤顶作为一个集中力,共计用26个千斤顶进行并联加载,对拱作用26个大小相等、加载速率相同的集中力(见图1)。千斤顶(集中力)作用在拱的外表面,与实际结构情况(次梁作用在拱的下半部)稍有不同。由于本次试验主要用于验证整体拱的受力情况和承载能力,可以忽略集中力作用点不同等因素。
为完成加载,设计了一个试验加载装置(见图2),主要组成部分为:底座,26套横梁拉杆,26个千斤顶及相应的油路、油泵,平面外支撑。

1.3 测试方法
测试内容:1)拱试件的径向变形。沿拱试件的轴线布置5个径向位移测点(见图3中测点S1~S5),用拉线式位移计测量测点处试件沿径向的位移。另外,在固定端布置位移计测量两端拱脚沿径向和轴向的位移,还布置位移计测量底座的变形(见图3中测点S6~S12)。由这些测点的位移测量结果,可以得到拱试件平面内的径向变形。2)拱身截面应变。沿拱试件的轴线布置5个应变测试截面,位置与径向位移测点相同。在每个应变测试截面,布置了6个轴向应变测点,7个横向应变测点。所有应变计都粘贴在试件钢管的外表面。3)集中力。在加载油路上,安装了1个液压传感器,用于测量1个千斤顶集中力的大小。
试验过程中,通过数据采集程序,进行数据采集。另外,还观察试件的受力变形情况和破坏形态。
2 试验结果
试验加载分为4个阶段:1)正常使用荷载试验,分级加载至22.63 kN(单个千斤顶的荷载,对应于使用时的80 kN/m2的面荷载)。2)弹性阶段加载,分级加载至50 kN。3)设计极限荷载,分级加载至87 kN(单个千斤顶的荷载,根据规范CECS 159∶2004矩形钢管混凝土结构技术规程和等效梁柱法按压弯构件计算得到)。4)极限承载力试验,分级加载至120 kN(单个千斤顶的荷载),然后连续加载至试件破坏。
第1阶段~第2阶段加载过程中和卸载后试件完好,未发现任何损坏现象。
第3阶段加载至60 kN时,试件发出轻微的声音;以后每级加载,都可以听到声音;卸载后检查,试件基本完好,未发现明显的损坏现象。
第4阶段加载至100 kN时,22号加载点附近钢管外壁附着的水泥浆薄层脱落;加载至120 kN时,试件各截面的应变增长较快,因此开始进行连续加载;加载至124.9 kN时,试件在22号与23号加载点之间的部位发生受压破坏,试件达到极限承载力,破坏时伴有剧烈响声。破坏后检查得到,破坏处钢管的四个侧面均向外鼓凸、焊缝撕裂,从裂口可见内部混凝土已压碎。另外,试件右面近拱脚处背面钢管鼓凸,该区域钢管与内部混凝土脱开。
3 试验结果分析
选取与破坏截面附近的截面1分析,截面1荷载—平均应变曲线见图4。

由图4可知,在第1阶段(0~A)截面的荷载与应变曲线基本为直线,加载至22.63 kN时(模拟0.8个大气压荷载),平均应变为184μ ε,根据试验记录的数据,卸载后应变基本回零,仍处于线弹性阶段。在第2阶段(A~B),截面的荷载与应变曲线基本为直线,加载至50.0 kN时,平均应变为 450μ ε,卸载后应变基本回零,仍处于线弹性阶段。在第3阶段(B~C),拱试件已有弹塑性变形,加载至87.0 kN时,平均应变为 950μ ε,卸载后有明显的残余变形,已进入弹塑性阶段。第4阶段(C~D)加载至 120 kN持载时,钢管内部混凝土损伤裂缝已经不稳定扩展,在荷载未增加的情况下,截面应变仍持续快速增长,加载至124.9 kN(极限承载力)时,平均应变为2 368 μ ε,拱试件达到破坏,根据先前拱身轴压试验结果,拱身轴心受压承载力平均值为1 676.7 kN,按结构力学计算方法,欲使拱试件达到轴心受压破坏,单个千斤顶荷载必须达到163.6 kN,本次试验极限承载力达到了轴心受压破坏荷载的76.3%。
根据各径向位移测点的数据画出各加载阶段拱的变形图见图5。

由位移数据以及图5可看出,在第1加载阶段~第2加载阶段,拱各处变形基本是对称的,对称点位移差距不大,这时拱是处于弹性工作阶段;当荷载逐渐增大,尤其是进入弹塑性工作阶段后拱的不对称变形越来越明显,对称点位移差距也逐渐加大,在拱发生破坏时,变形不对称性达到最高。
综合试验现象、各阶段荷载与应变、位移的关系,可以得出第1加载阶段~第2加载阶段,试件基本处于线弹性阶段,卸载时基本无残余变形,试件变形基本是对称的,当进入第3加载阶段,尤其是荷载大于60 kN时,试件因变形损伤发出响声,可以判断自60 kN开始试件已进入弹塑性阶段,进入弹塑性阶段后,试件变形加大,且不对称变形也越来越明显,试件由早期的轴心受压转变为压弯工作状态,最终发生失稳破坏。
4 结语
1)所施加的荷载(单个千斤顶的荷载)不大于 60 kN,试件基本处于线弹性阶段;荷载大于60 kN时,试件开始进入弹塑性阶段;拱试件的破坏形式为失稳破坏,破坏时钢管压弯、混凝土压碎,其破坏荷载达到了拱身试件的轴压破坏荷载的76.3%。2)在正常使用荷载(22.63 kN,模拟0.8个大气压荷载)作用下,试件截面的应变很小、变形也很小,试件仍处于线弹性阶段。根据相似关系,实际结构的单拱在相应的条件和荷载作用下,具有足够的承载力和安全储备,能够满足安全使用的要求。3)根据CECS 159-2004矩形钢管混凝土结构技术规程和等效梁柱法按压弯构件计算拱模型试件得出其极限轴力应控制在891.94 kN,换算成单个千斤顶荷载为87 kN,当荷载加载至87 kN时,拱模型试件已经进入弹塑性工作区,但持载时并未出现明显的应变增长,因此这时结构是处于稳定的弹塑性区域,试件在此荷载下是安全的。这说明按CECS 159∶2004矩形钢管混凝土结构技术规程和等效梁柱法来设计矩形钢管混凝土拱结构是可行且偏于安全的。4)拱试件的极限承载力为124.9 kN,换算成作用在屋面或外壳上的面荷载为442 kN/m2,相当于正常使用荷载(80 kN/m2)的5.5倍。根据相似关系,实际结构的单拱承载力可以达到在屋面或外壳上的面荷载为442 kN/m2。
[1]陈宝春.钢管混凝土拱桥设计与施工[M].北京:人民交通出版社,1999.
[2]邵旭东.钢管混凝土拱肋节段模型试验[J].长安大学学报(自然科学版),2003,23(4):34-37.
[3]CECS 159∶2004,矩形钢管混凝土结构技术规程[S].
[4]朱慈勉.结构力学[M].北京:高等教育出版社,2004.
[5]姚振纲,刘祖华.建筑结构试验[M].上海:同济大学出版社,1996.
[6]李德寅,王邦楣.结构模型实验[M].北京:科学出版社,1996.
——超集中力
—— 梁在集中力作用点处的剪力分析

