基于最小走时射线的LSQR 成像反演方法研究
赵火焱,赵明阶,黄卫东,李 建,李 勇
(1.重庆交通大学河海学院,重庆400074;2.重庆市交通工程监理咨询有限责任公司,重庆400042)
层析成像作为一种非破坏性的检测方法,概念是利用外部探测能量观察待测物的反应,藉由反应结果进而对待测物剖面进行成像的技术。其最早应用于天文显像(Bracewell,1956)、医学诊断与显微技术(DeRosier and Klug,1968)等,并逐渐应用于地球物理学和机械工业中。如今随着计算机技术和成像理论的发展,成像技术在土木工程无损检测中也日益发挥重要作用[1-3]。采用弹性波等激发源,根据实测波初至旅行时间及波的行进路径来反演待测体内速度分布的方法称为波速层析成像。
波速层析成像的概念可以由下面这个简单的数学公式来表示:

为确定波的行进路线ray,目前主要采用射线追踪技术,其理论基础是在高频近似条件下,波场的主能量沿射线轨迹传播。现有射线追踪方法有初至波旅行时法、线性旅行时插值法和最短路径法等。其中最短路径射线追踪算法最早由Nakanishi et al提出,Moser[4]对此方法做了全面研究。该方法基于图论和费马原理,其灵活而稳定,且适用于任意复杂介质模型,在弹性波正反演领域应用广泛[5-6]。
笔者根据最短路径射线追踪原理,并在离散网格单元过程中做出改进,采用FORTRAN语言和VB语言实现联合编程计算,然后通过建立数字模型来验证该方法的可行性。
1 波速层析成像系统的软件编制
1.1 建立速度网格和射线网格
为实现编程计算,笔者将待测体离散化为N个二维矩形节点网格作为速度网格,并假定网格单元内速度v为均匀分布。第i个单元的初始速度值由旅行时观测值假定:该方法首先假定模型为均质,则射线传播路径为直线,由第j条射线的长度Dj为与这条射线对应的观测值的比值得到射线上的平均速度值,令通过某网格单元的所有射线的速度均值为该单元的初始速度值。该方法比假设初始速度值为均值的方法具有一定的优越性[7]。
将速度网格各边内插若干节点并与原节点网格共同形成射线网格。本文用到的射线网格模型是在Moser使用的网络模型的基础上每单元增加了4个角点,即每条边增加2个节点,这在一定程度上提高了射线精度。根据惠更斯原理,每个射线节点既作为接收点又作为新的震源向周围节点传播能量,波在各节点之间的旅行时由下式得出:

其中:tij、dij为节点间走时及间距;Sij为节点公共单元慢度。
1.2 Dijkstra最短路径射线追踪法
求解最短路径问题多采用F.W.Dijkstra[8]提出Dijkstra算法。在求从网络中的某一节点(源点)到其余各节点的最短路径时,该算法将网络中的节点分成3部分:未标记节点、临时标记节点和最短路径节点。算法开始时源点初始化为最短路径节点,其余为未标记节点,算法执行过程中,每次从最短路径节点往相邻节点扩展,非最短路径节点的相邻节点修改为临时标记节点,判断权值是否更新后,在所有临时标记节点中提取权值最小的节点,修改为最短路径节点后作为下一次的扩展源,再重复前面的步骤,当所有节点都做过扩展源后算法结束。具体算法描述如下:设在一非负权简单连通无向图G=[V,E,W ](V:顶点集;E:边集;W:边权值)中,D 为图G的邻接矩阵,求源点P0到其余所有节点P(i)的最短路径长度。①将V分为未标记节点子集N、临时最短路径节点子集T和最短路径节点子集S,每个节点上的路径权值为 D(i),初始化:S=P0,T=φ,N=V-C,D(0)=O,D(i)=∞;②更新:将新加入 S集合的节点P(s)作为扩展源,计算从扩展源到相邻节点的路径值。若该值比原值小,则替换原值,否则保持原值不变,将相邻节点之中的未标记节点归为临时标记节点,即T=T∪ P(i),N=N- P(i);③选择:在T中选择具有最小路径值D(s)的节点P(s),归入集合S中,即 S=S∪P(s),T=T-P(s);④迭代判断:若T=φ算法结束,否则转②。
1.3 建立JACOBI矩阵
JACOBI矩阵A(M,N)是反映速度节点与各条射线关系的矩阵,M为射线根数,N为速度网格单元个数。当最短射线路径确定后,A(i,j)即为第i条射线在第j单元中的长度。由于每条射线只通过少数几个单元,只对这几个单元的节点产生影响,故JACOBI矩阵是大型稀疏矩阵,并且通常是病态的。
1.4 反演计算
网格离散化后,第j条射线旅行时理论值Tt
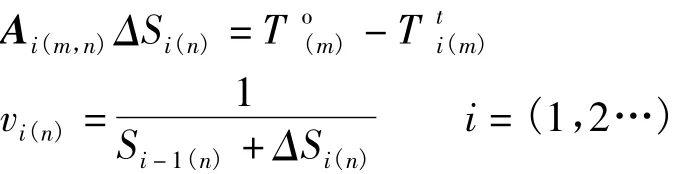
迭代方法有代数重建法(ART)、联合迭代重建法(SIRT)以及最小二乘正交分解法(LSQR)等几种。LSQR算法[9]计算速度快、易收敛,故采用此种方法。
2 假定物理模型
笔者设计了2个带有异常速度区域的假定物理模型。模型宽6 m,深8 m,离散网格间距0.5 m,每边内插9个节点,发射点22个,接收点24个,炮点间距均为0.5 m,左侧发射时顶部接收,顶部发射时左右两侧接收,射线布置图如图1。

图1 射线布置图Fig.1 Ray disposal figure
模型1(图2)设置水平低速异常带,带宽2 m,位置在顶面以下2 m,背景速度4 000 m/s,异常带速度为3 500 m/s。经7次迭代后射线图和色块图及波速三维图分别为图3~图5。

图2 模型1Fig.2 Model No.1

图3 经7次迭代射线图Fig.3 Ray after 7 times inversion

图4 经7次迭代后色块图Fig.4 Result after 7 times inversion

图5 经7次迭代后波速3D图Fig.5 Velocity 3D figure after 7 times inversion
模型2(图6)设置4个速度异常块,2个高速异常块,2个低速异常块,尺寸均为1 m×1 m。背景速度4 000 m/s,高低速异常块速度分别为4 500,3 500 m/s。经6次迭代后的射线图和色块图及波速三维图分别为图7~图9。
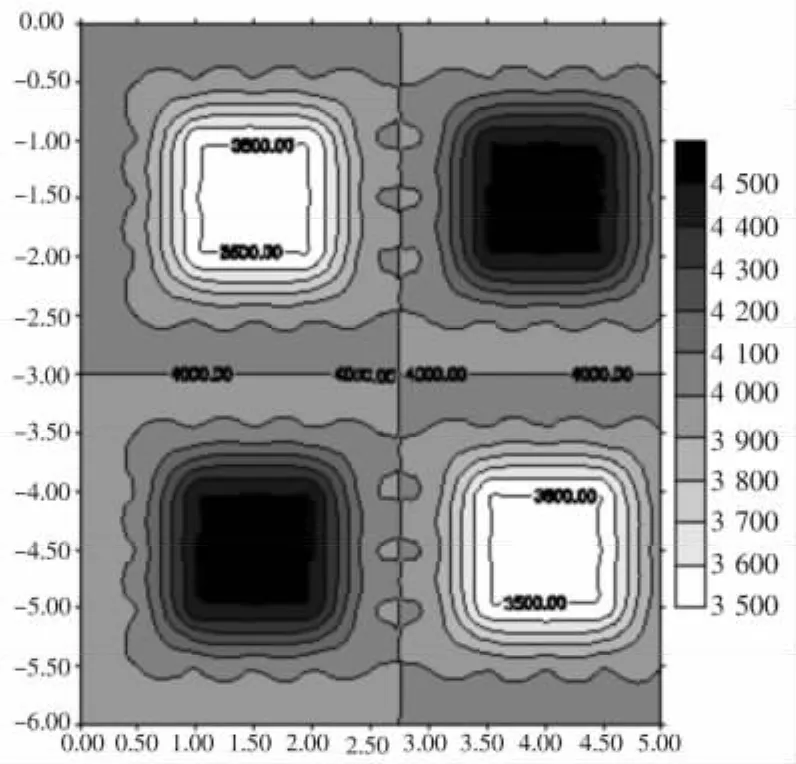
图6 模型2Fig.6 Model No.2
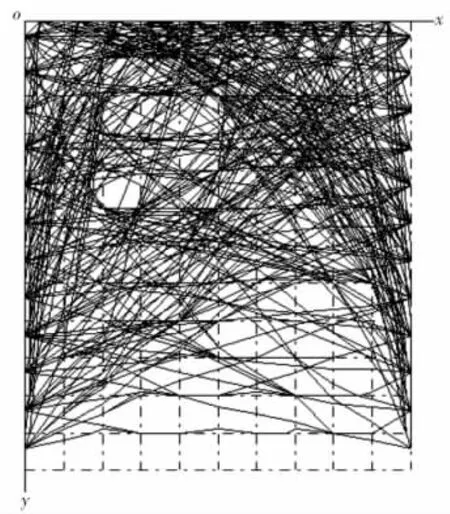
图7 经6次迭代后射线图Fig.7 Ray after 6 times inversion

图8 经6次迭代后色块图Fig.8 Result after 6 times inversion
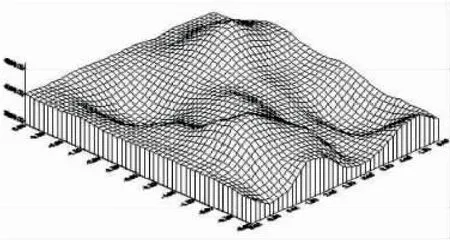
图9 经6次迭代后波速3D图Fig.9 Velocity 3D figure after 6 times inversion
通过观察图4及图8可见,成像结果能较好的反映速度异常区域的位置,但在形状和尺寸上存在失真,究其原因有以下几点:①本文模型中,射线是水平和倾斜的,缺少垂直方向或接近垂直方向上的射线,因此成像横向分辨率较垂向分辨率要高;②由于通过底部区域的射线数较少,导致这一区域的失真情况较明显;③由于在边界处数据的覆盖程度不足引起边界图像失真并影响反演的中间区域,使远离边界很大一段距离内的图象都发生畸变。
模型节点速度真值与反演值之间相关系数为:

模型1反演结果的平均相对误差为2.34%,相关系数为0.84,低速异常带相对误差为-4.4% ~12.5%;模型2平均相对误差为2.59%,相关系数为0.85,低速区节点相对误差为 -1.73% ~7.44%,高速区相对误差为-6.24% ~4.06%。节点相对误差如图10、图11。结果表明,异常区偏差较大,且结果值大都偏近于速度背景值;平均相对误差较小,相关系数值较高;成像结果能较好地反映模型值。

图10 模型1节点相对误差Fig.10 Node relative difference of model NO.1

图11 模型2节点相对误差Fig.11 Node relative difference of model NO.2
3 结论
对基于最小走时射线追踪方法和LSQR反演方法的波速层析成像从方法原理、假定物理模型等方面进行了研究,得出了以下2点结论:
1)基于最小走时射线追踪的LSQR波速层析成像方法可靠稳定,收敛性好,效率高。
2)由于射线分布不均及射线数据覆盖程度不足等原因引起图像局部失真。以上情况可通过完善射线布置情况和加密网格等方法得以改善。
[1]杨文采,杜剑渊.层析成像新算法及其在工程检测上的应用[J].地球物理学报,1994,37(2):239 -244.
[2]王五平,宋人心,傅翔,等.用超声波CT探测混凝土内部缺陷[J].水利水运工程学报,2003,56(5):56 -60.
[3]赵明阶,许锡宾.水工混凝土结构缺陷成像诊断的试验研究[J].水利学报,2007,38(2):198 -204.
[4]Moser T J.Shortest path calculation of seismic rays[J].Geophysics,1991,56(1):59 -67.
[5]张建中,陈世军,余大祥.最短路径射线追踪方法及其改进[J].地球物理学进展,2003(1):146-150.
[6]周兵,赵明阶.最小走时射线追踪层析方法[J].物化探计算技术,1992(2):124-130.
[7]段心标,金维浚.井间地震层析成像初始速度模型[J].地球物理学进展,2007(6):1831-1835.
[8]王志和,凌云.Dijkstra最短路径算法的优化及其实现[J].微计算机信息,2007(33):275-277.
[9]常旭,卢孟夏,刘伊克.地震层析成像反演中3种广义解的误差分析与评价[J].地球物理学报,1999(5):695-702.
——随钻钻孔电磁波层析成像超前探水设备及方法研究

