基于荷载传递法的锚杆锚固段荷载变形分析

许锡宾，刘 涛，褚广辉

(重庆交通大学 河海学院，重庆400074)

土木工程建设领域所面临的环境越来越复杂，需要抵抗灾害的要求越来越高，高切边坡、深基坑、复杂环境下的隧洞等工程都需要有一种安全可靠的支护技术。锚固技术能较充分地发挥和提高岩土体的自身强度和自稳能力，显著缩小结构物体积和减轻结构的自重，因此，有效控制岩土工程的变形，就成为提高岩土工程稳定性和解决复杂岩土工程问题最经济有效的方法之一。

对于锚杆的锚固机理的研究，目前还没有统一的理论，国内外主要是从两个方面对其进行展开研究［1－3］:①锚固段载荷传递机理，特别是注浆岩石锚杆中锚杆与灌浆体、灌浆体与周围岩体之间黏结应力的分布和传递机理的研究，这是从微观方面进行分析;②宏观分析研究，从锚固体加固效果角度出发研究岩土锚固作用机理。很多学者利用力学理论对锚固段荷载传递机理进行了解析分析。尤春安［4］基于Mindlin问题的位移解，推导了全长黏结式锚杆剪应力、轴向载荷等应力分布的弹性解;张季如、唐保付等［5］在假定锚固体与岩土体之间的剪切力与剪切位移呈线性增加关系的基础上，建立了锚杆荷载传递的双曲函数模型;杨庆等［6］基于 Boussinesq问题的位移解，推导出了和基于Mindlin问题的位移解相同的结果。

笔者引入在桩基沉降计算中常用的荷载位移法对锚杆锚固段进行分析，推导其荷载传递的基本微分方程;再结合开尔文(Kelvin)问题的位移解，推求锚固段的应力分布函数。以此试图能够对锚固段的荷载传递机理有更深一步的认识。

1 荷载传递法的基本原理

荷载传递法［7］首先是由Seed和Reese在1955年提出的，是研究桩基础的一种最普遍的方法。其基本概念是把桩看作由许多弹性单元组成，每一单元与土体之间(包括桩尖)都用非线性弹簧联系(图1)，这些非线性弹簧表示桩侧摩阻力(或桩尖阻力)与剪切位移(或桩端位移)之间的关系，通常统称为荷载传递函数或τ－z曲线。一旦桩土间的这种关系曲线获得后，就可以求得在竖向荷载下桩侧摩阻力和桩身轴力分布以及桩身各截面处的位移。

图1 荷载传递法力学模型Fig.1 Sketch of load transfer method

2 基本微分方程

笔者将锚杆视做桩，采用荷载传递法来推导锚杆锚固段荷载传递的基本微分方程，结合Kelvin问题的位移解来推求锚固段的剪应力与轴力分布函数。

2.1 Kelvin模型

在无限体内一点O承受集中力P的作用，此一问题即为Kelvin问题［8］，它对应的基本解是Kelvin解，利用这些基本解可以解决很多全空间和半空间的受力问题。Kelvin力学模型见图2。设集中力P沿z方向作用在坐标原点O，边界条件应满足:

1)在无穷远处所有应力分量均趋于0;

2)在O点处应力的奇异性相应于集中力的幅度P。

Kelvin问题沿z方向的位移u(z)为:

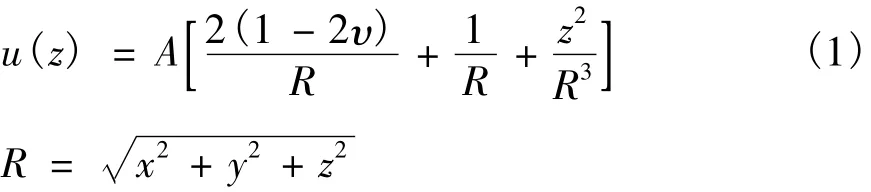
图2 开尔文问题模型Fig.2 model of Kelvin problem

锚杆埋置到稳定岩层，深度较深，已有的研究表明在锚杆锚固段远端应力分布很小并趋近于0，可以认为锚固段处于无限体中。根据荷载－位移互等定理，作用于o点的力P在M点产生的位移等于M点的作用力P在o点产生的位移。并假定预应力锚杆的锚固段与z轴重合，锚固段的始端点与o点重合，此时x=y=0，对式(1)简化，则得到在集中力P的作用下锚杆锚固段内任意一点处z所产生的位移:

2.2 基本微分方程

将锚杆视作桩，来分析其荷载传递过程。其受力与图1相似，取图1中的微段进行受力分析:

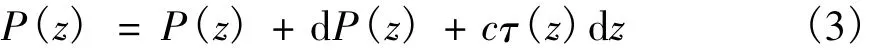
式中:c为锚杆体的周长，c=πD(D为锚杆体直径)。

式(3)简化为:

微元体受荷后所产生的弹性变形为:

式中:Eg、Ag分别为锚杆体的弹性模量和截面积。

由式(4)、式(5)可得:

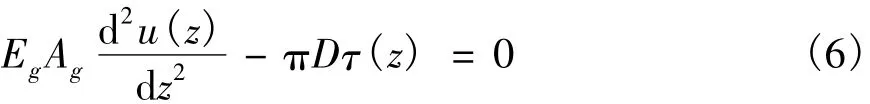
即为基于荷载传递法的锚杆锚固段的基本微分方程。

2.3 锚固段荷载传递函数(τ－z曲线)

结合式(2)及式(6)，可以得到锚固段的剪应力的分布函数:

对式(7)沿锚固段长度积分即得锚杆锚固段的轴力分布函数:

式(7)、式(8)即为锚杆锚固段的剪应力、轴力分布函数。

3 锚固段受力特性分析

3.1 锚固段的受力特征

从剪应力及轴力分布函数可以看出，锚杆体的弹性模量、岩土体的剪切模量、锚杆体的直径(孔径)、外荷载等因素影响着锚固段剪应力及轴力的分布。在此考虑锚杆体和岩体的弹性模量分别为Eg=30 GPa，E=0.5 GPa，岩体泊松比 υ =0.25，岩体剪切模量。不同的P及D的情况下锚固段的应力分布特征分析如下。

3.1.1 P为定值，D不同的情况

取 P=100 kN，D 分别为0.15，0.2，0.25，0.3。将数值分别带入式(7)、式(8)，得到锚固段应力分布曲线，如图3、图4。

图3 不同直径时的剪应力分布曲线(P=100 kN)Fig.3 Relation between shear stress and anchored section length(P=100 kN)

图4 不同直径时的轴力分布曲线(P=100 kN)Fig.4 Relation between axial force and anchored section length(P=100 kN)

从图3、图4中可以看出，锚固段应力分布是很不均匀的，剪应力和轴力的最大值都出现在锚固段端部，随着锚固段长度的增加，剪应力和轴力都呈下降趋势，在锚固段远端趋于0。随着锚杆体直径D的增大，剪应力和轴力在锚固段端部都急剧增大，并且在较大的锚杆体直径D的情况下应力沿锚固段长度衰减得较快。

应力主要分布在锚固段前端，表明锚固体直径的增大对锚固段的应力分布改善并不显著。沿着锚固段长度方向，剪应力在z为3 m处已相差不大，轴力在z为5 m处也比较接近，说明锚固段超过一定长度后，对于增加锚杆的工作性能的效果并不明显。

3.1.2 D为定值，P不同的情况

取 D=0.2 m，P 分别为 50，100，150，200 kN。将数值分别带入式(7)、式(8)，得到锚固段应力分布曲线，如图5、图6。

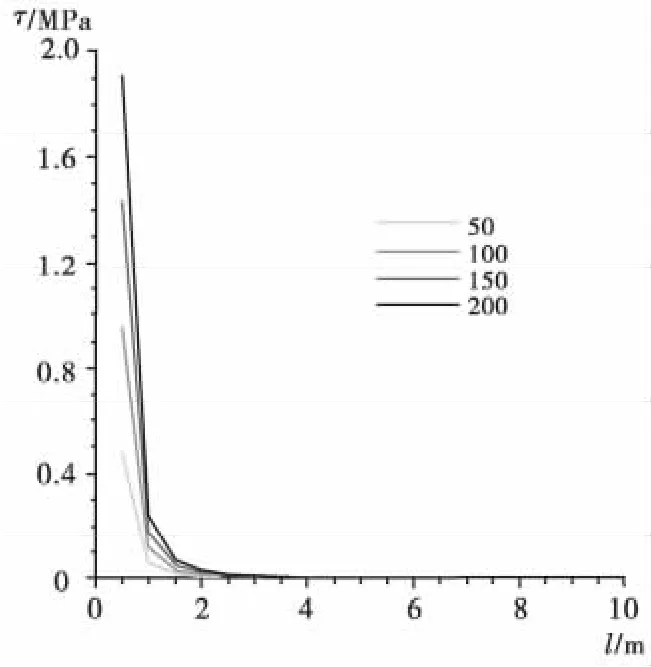
图5 不同外载时的剪应力分布曲线(D=0.2 m)Fig.5 Relation between shear stress and anchored section length(D=0.2 m)

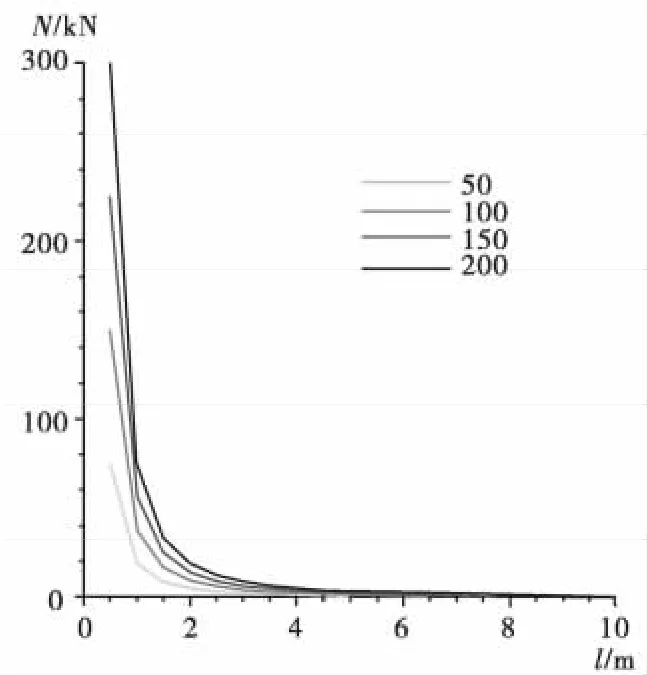
图6 不同外载时的轴力分布曲线(D=0.2 m)Fig.6 Delation between axial force and anchored section length(D=0.2 m)

从图5、图6中可以看到应力分布曲线情况与第1种情况大致相似，因为在分布函数中剪应力与轴力分别是关于锚固段长度z的－3次、－2次幂函数，曲线近似呈双曲线型式。从图中还可看出，在不同的P的情况下可以得到与第1种情况类似的结论。

3.1.3 不同的Eg/G值的情况

以上两种情况没有考虑不同的Eg/G值的影响。下面取几组不同的Eg/G值来看看锚固段的应力分布。Eg/G 值分别取为 500，300，150，75，50，设P=100 kN，D=0.2 m，得到的应力分布曲线如图7、图8。

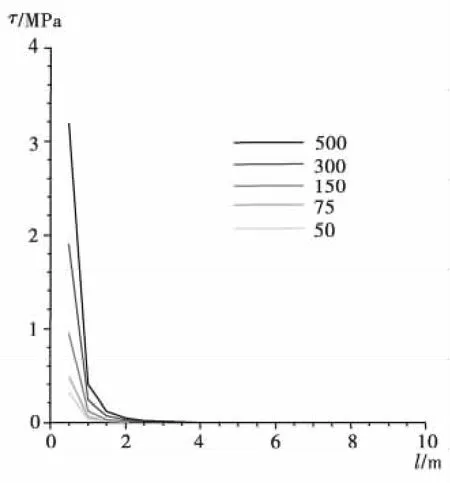
图7 剪应力分布曲线(不同的Eg/G值)Fig.7 Relation between shear stress and anchored section length(different values of Eg/G)

图8 轴力分布曲线(不同的Eg/G值)Fig.8 Relation between axial force and anchored section length(different values of Eg/G)

从图7、图8中可看出，Eg/G值越大，锚固段前端的应力衰减就越迅速，而随着Eg/G值的减小，锚固段前端的应力急剧下降，在z为3～4 m时逐渐趋缓，至锚固段远端接近于0。也就是说，Eg/G值越小，锚固段所受到的最大剪应力值就越小，沿锚固段应力的分布就越均匀，但同时其应力作用范围也较小，这样容易在界面处发生破坏，导致锚固系统失效;Eg/G值越大，锚固段顶端所受到的最大剪应力值就越大，应力集中现象就越明显，其应力分布的范围就越广，但不均匀程度也相应较大。

3.2 锚固段受力影响因素分析

从得到的锚杆锚固段荷载传递函数可知，锚杆体的直径(孔径)、外荷载、锚杆体弹性模量与岩体剪切模量的比值等因素影响着锚固段的应力水平。

1)锚杆所受剪应力与锚杆直径(孔径)成正比，锚固段在较大的孔径情况下应力分布范围有所扩大，但不能一味靠加大杆体尺寸来提高锚杆的工作性能，随着直径的增加，会使锚杆所受的最大剪应力快速增加。

2)在较高的P值条件下，锚杆相应的剪应力很大，特别是在锚固段前端;应力沿锚固段长度方向衰减的速度更加迅速。

3)锚杆体弹性模量与岩体剪切模量的比值对锚固段应力分布的影响有很大关系。比值越小，锚固段所受到的最大剪应力值就越小，越有利于锚固段应力的均匀分布，但同时其应力作用范围也较小;比值越大，锚固段顶端所受到的最大剪应力值就越大，其应力分布的范围就越广，但不均匀程度也相应较大。

4 结语

笔者在对锚固段的受力特性分析中引入荷载传递法，通过荷载传递法的基本原理推导了锚固段荷载传递的基本微分方程，结合开尔文问题的位移方程推求了锚固段的荷载传递函数，得到了以下一些结论:

1)锚固段应力分布的影响因素与锚杆体的弹性模量、岩体剪切模量、锚杆体直径(孔径)、外荷载等因素有关。锚固段的剪应力大小与孔径及外荷载呈正比，较大的孔径与外荷载，其应力作用范围较大;锚杆体弹模与岩体剪切模量比值越小，锚固段所受到的最大剪应力值就越小，越有利于锚固段应力的均匀分布。

2)锚固段应力分布非常不均匀，应力最大值出现在锚固段始端，并沿锚固段长度方向逐渐缩小，在锚固段远端趋于0。表明锚固段过长对于改善锚杆的工作机制没有多大作用，往往还造成工程浪费。

3)通过Kelvin位移方程应力分布函数具有奇异性，计算结果在锚固段端部会出现应力无穷大的现象，不能表现出锚固段起始端的实际受力特征。

4)分析将锚索与灌浆体看作一个整体，没有考虑它们之间的相互作用。而预应力锚杆在受到外荷载的作用时，在灌浆体与锚索之间产生了相互作用力，此相互作用力对灌浆体施加了一个反作用力并传递到周围岩体上，这就存在灌浆体和岩体之间、灌浆体和锚索之间两个界面上的作用力，其相互之间的作用对于锚固段的荷载传递机理有何影响，在以后的工作中还有待进一步的研究。

［1］程良奎，韩军，张培文.岩土锚固工程的长期性能与安全评价［J］.岩石力学与工程学报，2008，27(5):865 －872.

［2］程良奎.岩土锚固研究与新进展［J］.岩石力学与工程学报，2005，24(21):3803 －3811.

［3］张乐文，汪稔.岩土锚固理论研究之现状［J］.岩土力学，2002，23(5):627－631.

［4］尤春安.全长黏结式锚杆的受力分析［J］.岩石力学与工程学报，2000，19(3):339 －341.

［5］张季如，唐保付.锚杆荷载传递机理分析的双曲函数模型［J］.岩土工程学报，2002，24(2):188 －192.

［6］杨庆，朱训国，奕茂田.全长注浆锚杆的解析本构模型研究［C］//中国岩石力学与工程学会东北分会.第九届全国岩石力学与工程学术大会论文集.北京:科学出版社，2006.

［7］钟闻华.深长桩荷载传递特性与相互作用理论及应用研究［D］.南京:东南大学，2005.

［8］杜庆华，余寿文，姚振汉.弹性理论［M］.北京:科学出版社，1986.