考力代羊体重生长的遗传参数估计

李秀丽 孙红梅 刘文忠

（①山东畜牧兽医职业学院 潍坊 261061 ②大盛畜牧兽医管理站③山西农业大学动物科技学院)

考力代羊是世界著名的半细毛羊品种之一，原产于新西兰。它的肉用体型较明显，肉质较好，全身被毛白色，有闭合型毛被，相对早熟的特点。我国从20世纪40年代中期、60年代中期和80年代后期先后从新西兰和澳大利亚引进考力代羊，除进行纯种繁育外，还作为主要父系品种，用来改良本地绵羊，已参与培育了东北半细毛羊、陵川半细毛羊、贵州半细毛羊、云南半细毛羊等新品种或类群，使本地绵羊羊毛质量大大改善，剪毛量显著提高[1]，表现出良好的适应性和生产性能，弥补了我国羊毛和羊肉产品短缺的状况。

本研究拟对考力代羊生长性状的遗传参数估计，旨在了解考力代羊生长性状的遗传规律和遗传背景，掌握影响生长性状的遗传和非遗传因素。根据不同月龄生长性状的遗传力估值，可为考力代羊的育种规划提供依据。

1 材料与方法

1.1 材料

1.1.1 试验动物及数据来源 本研究所用数据来自山西省沁水示范牧场考力代羊初生、断奶、8月龄、周岁和18月龄等5个关键时间的体重数据(表1)，原始数据集涉及1 480个个体，其中有记录的个体数1 330，经剔除系谱不清或记录不详的个体后，共1 418个个体，其中有记录的个体数1 269，共有3 332个记录。基础群个体数149只。

表1 生长性状的数据集概况

1.1.2 数据预处理 ①剔除系谱不清、记录不详的个体；②剔除超出平均值±2SD范围之外的数据；③断奶重统一校正至4月龄，校正公式为：

1.1.3 自然生态环境及饲养管理方式 沁水示范牧场位于山西省太行、太岳、中条三山之间，海拔900～1 200m，属暖温带半湿润大陆性气候。

每年夏秋以放牧为主，并根据体况和不同生理状况适当补饲精料，草地类型为白羊草灌草丛草地，主要草种组成见靳宗立等(1992)[2]；冬春期间采用放牧加舍饲方式。舍饲日粮由专家根据具体情况配制而成，主要由苜蓿草、禾本科青干草、青贮、胡萝卜，混合精料等。

每年剪毛1次，时间大约为4月下旬。每年9～11月配种，2～4月产羔。5～8月药浴3～5次，春秋全面防疫和驱虫两次，并在羔羊断奶和周岁时各驱虫1次。舍饲期间每隔2月左右修蹄1次。

1.2 方法

1.2.1 单性状参数估计 分别将生长性状的5个不同月龄的体重测定值作为5个不同性状，用混合模型来估计其方差组分和遗传参数。

1.2.1.1 遗传分析中的9个动物模型 模型1 y=Xb+Z1a+e；模型2 y=Xb+Z1a+W1p+e；模型3 y=Xb+Z1a+W2c+e；模型4 y=Xb+Z1a+Z2m+e、(Cov(a,m′)=0)；模型5 y=Xb+Z1a+Z2m+e、(Cov(a,m′)=Aσam)；模型6 y=Xb+Z1a+Z2m+W2c+e、(Cov(a,m′)=0)；模型7 y=Xb+Z1a+Z2m+W2c+e、(Cov(a,m′)=Aσam)；模型8 y=Xb+ Z1a+Z2m+W1p+W2c+e、(Cov(a,m′)=0)；模型9 y=Xb+Z1a+Z2m+W1p+ W2c+e、(Cov(a,m′)=Aσam)。式中，y为个体性状的观察值向量；b、a、m、p和c分别为固定效应、直接加性遗传效应、母体加性遗传效应、个体永久环境效应和母体永久环境效应向量；X、Z1、Z2、W1和W2分别为相应效应的关联矩阵；e为残差效应向量；Cov(a,m′)为加性直接遗传效应和母体遗传效应间的协方差矩阵；σam为直接加性遗传效应和母体遗传效应间的协方差；A为分子血缘相关矩阵。且有：。其中，I为单位矩阵，和分别为直接加性遗传方差、母体加性遗传方差、个体永久环境方差、母体永久环境方差和残差方差。

1.2.1.2 统计分析软件 用DFREML软件的DFUNI程序[3]，采用平均信息REML (AIREML)[4]的算法估计方差组分和遗传力，收敛标准为1×10-8。

1.2.1.3 最宜模型的选择 模型间的比较分两种情况：①随机效应数相同时，可直接用对数约束似然函数最大值比较，似然值大的较好；②随机效应数不同时，用似然比检验(LRT)来决定，即-2(logLi-logLj)服从自由度为ninj的χ2分布。其中，logLi和logLj和分别为模型i和j的约束最大似然函数值的对数；ni和nj分别为模型i和j的随机效应数[5,6]。然后将分析所得的最宜模型用作后续多性状参数估计的模型。

1.2.2 多性状参数估计 （1）模型和模型中的固定效应。模型为单性状分析所得的最宜模型，模型中的固定效应为单性状分析筛选固定效应后所得的所有显著非遗传因素的主效应(表2)，即出生年份、出生月份、性别和出生类型。（2）遗传参数估计。分2种情况：①不考虑误差间的协方差；②考虑误差间的协方差，用DFREML软件DXMUX程序[3]，采用AIREML算法[4]，收敛标准为1×10-8，1次估计5个不同性状间的协方差组分和遗传相关，2种情况下的遗传力估值与单性状遗传力估值进行比较。

表2 固定效应的水平数

2 结果

2.1 单性状遗传分析

2.1.1 模型中所包括的固定效应 经GLM分析，初生重遗传分析模型中包含的固定效应为出生年份和出生类型；断奶重、8月龄重、周岁重和18月龄重遗传分析模型中应包含的固定效应为出生年份、出生月份、性别和出生类型(表3)。

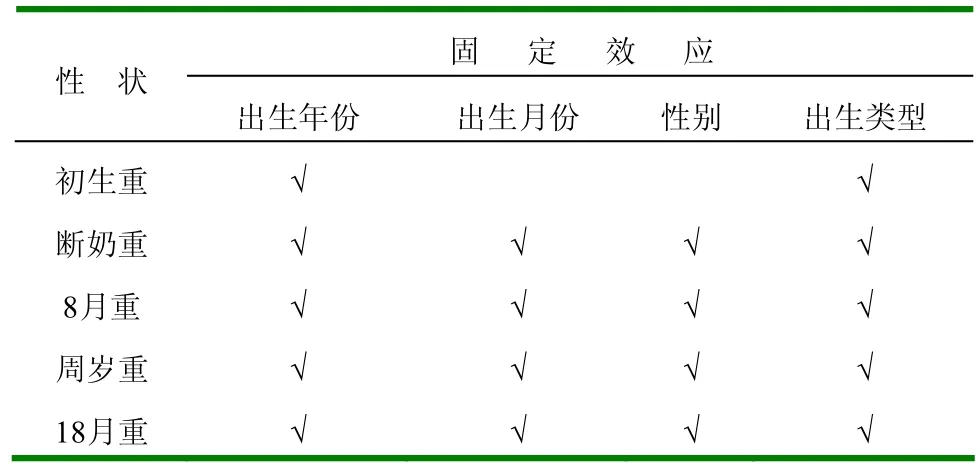
表3 不同性状遗传参数估计的模型中所包括的固定效应

2.1.2 不同模型的参数估值 （1）初生重。不同模型下初生重的参数估值见表4。①模型1和模型2的遗传力没有变化，说明个体永久环境效应对遗传力估值没有影响。②模型3在模型1的基础上考虑了母体永久环境效应，其遗传力有所下降。③考虑母体遗传效应的模型，无论考虑不考虑直接-母体遗传相关，其直接遗传力几乎没有变化，但比不考虑母体遗传效应时的遗传力估值小。考虑直接-母体遗传相关时母体遗传力较小，直接-母体遗传相关为正值，且母体遗传力比相应的直接遗传力大。若在此基础上再考虑母体永久环境效应，此时，无论考虑不考虑个体永久环境效应，母体永久环境方差在初生时几乎为0。（2）断奶重。不同模型下断奶重的参数估值见表5。①模型1和模型2下的断奶重与初生重情况相同，即个体永久环境效应对遗传力估值没有影响。②模型3下的断奶重也与初生重情况相同，即考虑母体永久环境效应时，遗传力有所下降。③当模型中考虑母体遗传效应时，若不考虑直接-母体遗传相关，直接遗传力较其它模型小，这主要是由于直接-母体遗传相关为负值所造成的。（3）8月龄重。不同模型下8月龄重的参数估值见表6。①模型1、模型2和模型3下的遗传力变化与初生重和断奶重情况相同，即个体永久环境效应对遗传力估值无影响，母体永久环境效应可使其减小。②考虑母体遗传效应的模型，直接遗传力较其它不考虑母体遗传效应的模型小，且考虑直接-母体遗传相关比不考虑直接-母体遗传相关时，直接遗传力稍大，相应的母体遗传力也稍大，直接-母体遗传相关为适度大的负值。（4）周岁重。不同模型下周岁重的参数估值见表7。①模型1、模型2和模型3下的个体永久环境效应与母体永久环境效应对周岁重的遗传力估值影响情况与初生重、断奶重和8月龄重相同。②考虑母体遗传效应时，遗传参数估值与8月龄情况相同，只是考虑直接-母体遗传相关时，其母体遗传力比不考虑直接-母体遗传相关时大得多，且直接-母体遗传效应间的负遗传相关达最大值。（5）18月龄重。不同模型下18月龄重的参数估值见表8。①模型1、模型2和模型3下，个体永久环境效应和母体永久环境效应对遗传力估值的影响与初生、断奶、8月龄和周岁重的影响情况相同。②考虑母体遗传效应时，遗传参数估值与周岁重情况相同。

表4 不同模型下初生重的参数估值

表5 不同模型下断奶重的参数估值

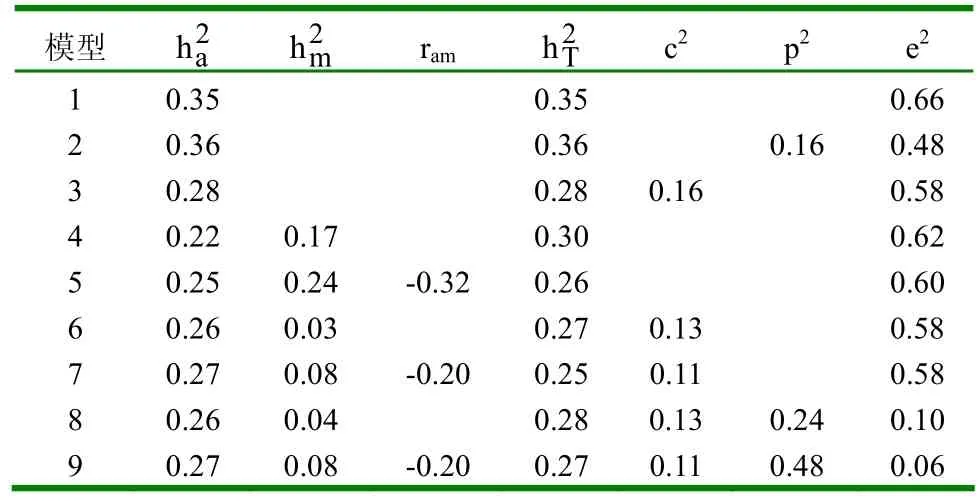
表6 不同模型下8月龄重的参数估值

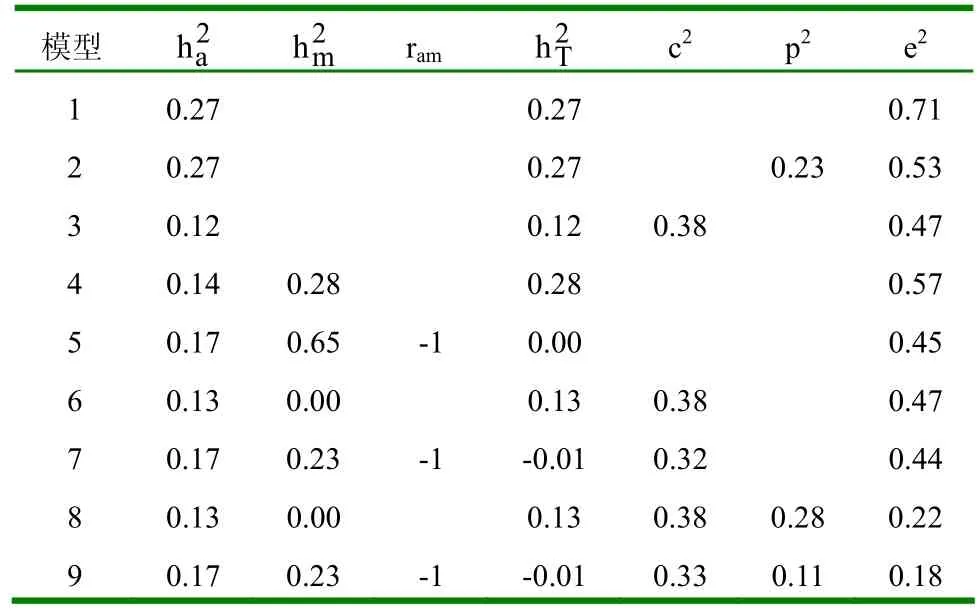
表7 不同模型下周岁重的参数估值

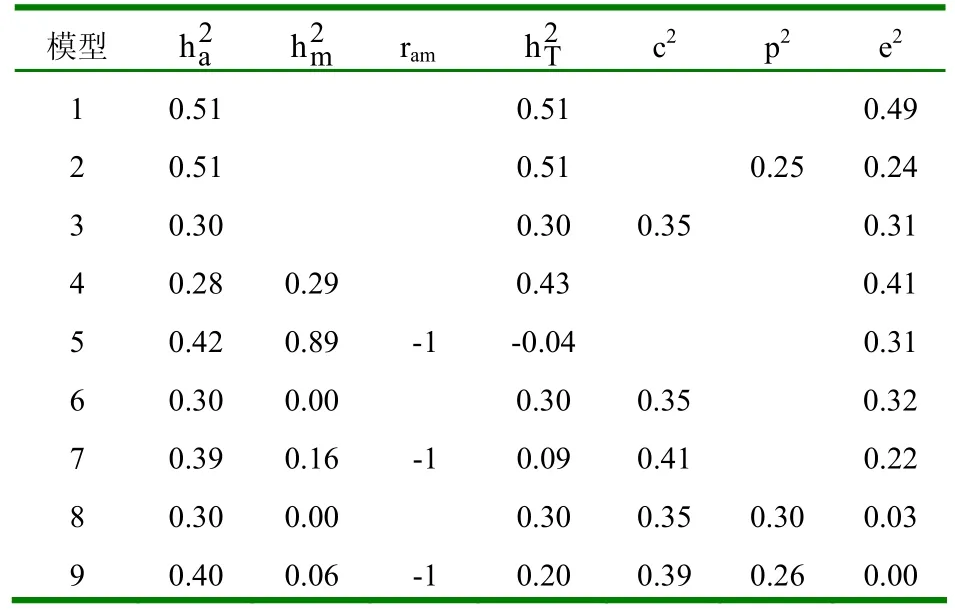
表8 不同模型下18月龄重的参数估值

2.1.3 模型的选择结果 含两个随机效应数的模型2、3、4中，模型3的似然值较大，以模型3为宜，含三个随机效应数的模型5、6中，以模型6为宜，含4个随机效应数的模型7、8中，以模型7为宜，模型1、3、6、7、9的似然比检验结果，以模型3为宜(表9)，所配合的效应为直接加性随机效应和母体永久环境随机效应。

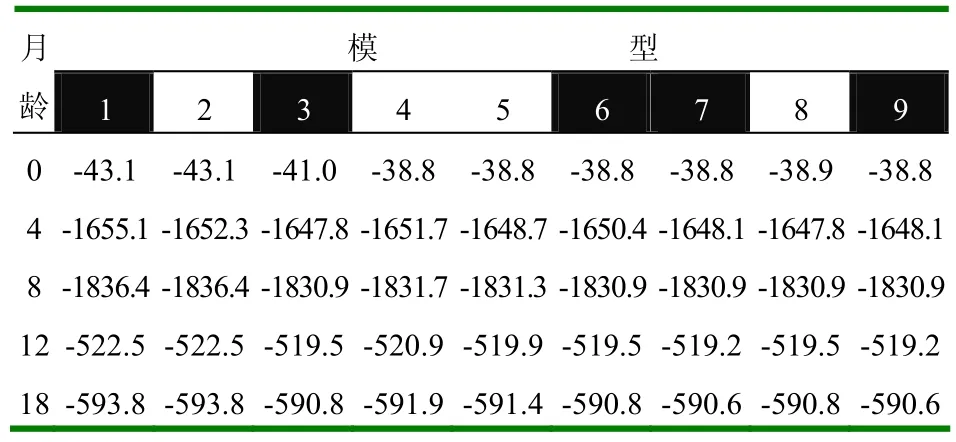
表9 不同模型下各性状遗传力的对数约束最大似然值

2.1.4 最宜模型下的参数变化 从初生到18月龄的参数变化情况(表3～表8)来看，初生重遗传力较大，从初生到断奶，体重遗传力变化呈下降的趋势；从断奶到8月龄，体重遗传力变化不大；8月龄到12月龄，体重遗传力急剧下降；12月龄到18月龄呈增大趋势(图1左)；c2从初生到8月龄变化不大，从8月龄到12月龄则急剧增大，12月龄到18月龄又开始下降(图1右)。

最宜模型下的遗传力为：初生重0.32、断奶重0.27、8月龄重0.28、周岁重0.12、18月龄重0.3。

图1 左、右图分别为单性状分析下体重的遗传力(h2)和母体永久环境方差(c2) （母体永久环境方差表示为与表型方差之比)

2.1.5 最宜模型下的方差组分估值 最宜模型下的方差组分估值见表10，这些估值作为多性状分析的初值。

表10 最宜模型下的方差组分估值

2.2 多性状遗传分析

2.2.1 遗传力 多性状遗传分析所得遗传力估值见表11。若不考虑误差间的协方差，则与单性状遗传力估值不一致，明显的较大；若考虑误差间的协s方差，则与单性状遗传力估值基本一致，呈中等大小；不考虑误差间协方差比考虑误差间协方差的遗传力估值明显偏高。

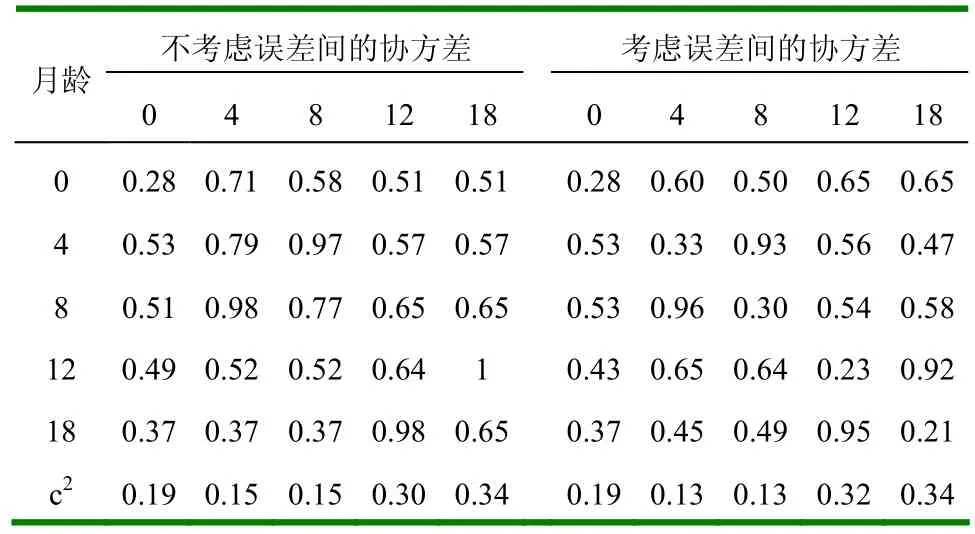
表11 多性状遗传分析的参数估值

2.2.2 母体永久环境效应 由表11和图2可见，c2在考虑与不考虑误差间协方差的两种情况下没有多大的变化。与单性状遗传分析结果比较，大小和变化趋势基本一致。

图2 左、右图分别为不考虑和考虑误差间协方差时的母体永久环境方差（母体永久环境方差表示为与表型方差之比）

2.2.3 相关 各性状间的遗传和母体永久环境相关见表11，可见月龄相近的二性状间相关较大，月龄相差越大，其间的相关越小。初生重与断奶重的遗传相关比与其它性状的遗传相关较大。表型相关也有同样的情况(表12)。本研究所有性状间的遗传相关和表型相关都为正值。由表11和表12可看出，不考虑误差间的协方差时，遗传相关、母体永久环境相关和表型相关相对较大。

表12 性状间的表型相关

3 讨论与结论

3.1 关于固定效应的筛选

当模型中包含的固定效应经GLM过程筛选后，计算过程中涉及的方程组较小，计算速度大大加快，又降低了耗机时间，并且大多月龄体重的误差方差与表型方差比也较小。因此，分析前已进行固定效应的筛选为宜，尤其是对于大的数据集，更应该做这一步工作。

若固定效应不经筛选或对于大数据集，包含固定效应多时，是否对参数估值有显著影响，有待进一步研究。

3.2 关于遗传力估值

3.2.1 单性状遗传力估值 本文中考力代羊生长性状的遗传力呈中等大小，这与Forgarty (1995) 报道兼用绵羊品种的遗传力范围[7]一致。Jara (1998) 报道，智利考力代羊的初生重和断奶重遗传力分别为0.32±0.07和0.37±0.10[8]，与本文结果也一致。因此，对考力代羊任何月龄的体重进行选择都能够获得一定的进展。

3.2.2 关于母体效应 本研究所得最宜模型包括母体效应，且当模型中不考虑母体效应时，直接遗传力被过高地估计，这与刘文忠关于安哥拉山羊生长性状的研究[5]中报道一致。模型中考虑母体遗传效应且不考虑效应间遗传相关时，母体遗传力由大到小变化，周岁和18月龄几乎为0，与Robison (1981) 报道母体遗传效应在随年龄逐渐减小[9]一致。另外羔羊早期母体遗传力大于直接遗传力，与Nasholm和Danell (1994)[10]报道一致。因此，对生长性状的动物分析模型中应该包括母体效应，否则误差过大。

3.2.3 多性状遗传力估值 当不考虑误差间协方差时，多性状遗传力估值比单性状遗传力估值高，而母体永久环境方差与表型方差的比则在两种情况下没有多大变化，所以遗传参数过高的估计，主要是由于部分误差效应被合并到了遗传效应里面。因此，分析遗传参数时，应该考虑误差间的协方差。

3.3 关于遗传相关

考虑误差间协方差时，所有性状间的遗传相关估值均为正值，表明对任何月龄体重的选择都将有利于其它月龄体重的提高。

3.4 关于环境效应

对于以放牧为主的生产系统，应该合理考虑大的环境效应的影响。

[1]孙清, 勃利种羊场: 考力代羊(下载).

[2]靳宗立等. 1992. 安哥拉山羊在黄土高原白羊草灌草丛放牧时的采食特性[J]. 山西农业大学学报(专辑): 9-13.

[3]Meyer, K. 1997. DFREML Version 3.1. User Notes. 29pp.

[4]Gilmour, A.R., et al. 1995. Average information REML: An efficient algorithm for variance parameter estimation in linear mixed models.Biometrics. 51: 1440-1450.

[5]刘文忠. 2001. 安拉山羊主要性状的遗传分析与选种方法研究[D].博士学位论文.

[6]Meyer, K. 2000. Estimating direct and maternal covariance function for growth of Australian beef calves from birth to weaning. Genet. Sel.Evol. (Submitted).

[7]Fogarty, N.M. 1995. Genetic parameters for live weight, fat and muscle measurements, wool production and reproduction in sheep; a review. Animal Breeding Abstracts. 63: 101-143.

[8]Jara, A., et al. 1998. Direct and maternal genetic effects for birth,weaning and 14-month weights of Corriedale breed in Magallanes. In:Proc. 6th World Congr. Genet. Appl. Livest. Prod., Armidale, 24: 181-184.

[9]Robison, O.W. 1981. The influence of maternal genetic effects on the efficiency of selection. A review. Livest. Prod. Sci. 8: 121-137.

[10]Nasholm, A., and O. Danell., 1994. Maternal genetic effects on lamb weights. In: Proc. 5th World Congr. Genet. Appl. Livestock Prod. 18:163-166.