遗传算法在秩亏自由网平差中的应用研究
唐立强
(湖南省水利水电勘测设计研究总院 长沙市 410007)
1 问题的提出
在经典间接平差中,必须要有足够的起算数据。当控制网中仅含必要的起算数据时,我们称之为自由网;当控制网中除必要起算数据外,还有多余起算数据时,我们称之为附合网。不管自由网还是附合网,在间接平差时,当所选的待定参数独立时,误差方程的系数矩阵B总是列满秩的,相应的法方程系数阵N=BTPB为一满秩对称阵,故法方程有唯一解。
在实际工程应用中,我们经常遇到一种具有特殊用途的控制网,它没有起算数据并以待定点的坐标作为参数。显然,由于缺乏确定控制网坐标的基准,这种网的误差方程的系数矩阵B不是列满秩的,相应的法方程系数阵N=BTPB为奇异阵。这种网被称为秩亏自由网。秩亏自由网的法方程系数阵N奇异,即│N│=0,故N的凯利逆N-1不存在,法方程有无穷解[1]。因此在求解此类问题时一般采用附加d(d为法方程秩亏数)个基准条件,且附加的基准条件与法方程N线性无关。基准条件的确定依据不同的网型,需要进行大量的前期计算工作,而且把基准条件方程与法方程联立进行参数估计时,涉及复杂的矩阵运算。鉴于此,有必要研究一种计算更加简单、有效的参数估计方法。
遗传算法(Genetic Algorithms),简称 GA,是人类向其自身演化这一宏观过程学习的结果,是一种更为宏观意义下的仿生算法,它模仿的机制是一切生命与智能的产生与进化过程。它通过模拟达尔文“优胜劣汰、适者生存”的原理激励好的机制;通过模拟孟德尔遗传变异的理论在迭代过程中保持已有的结构,同时寻找更好的结构[2]。与其它搜索算法相比,GA具有智能性、良好的并行性、很强的通用性、全局优化性、稳健性、可操作性、简单性的优点,体现出很强的寻优能力。本文提出一种基于遗传算法求解秩亏自由网平差的新算法。
2 问题的数学描述
秩亏自由网平差的法方程组用下式表示:

其中 法方程系数阵N=BTPB为t×t维的奇异方阵,参数向量 X=(x1,x2,…,xt)T,常数项向量 W=(w1,w2,… ,wt)T,t为未知参数的个数。
令 F(X)=NX-W,其中 F(X)=(f1(X),f2(X),…,ft(X))T,为了方便用遗传算法来求解奇异方程组 (1),将方程组(1)的求解转化为一个多维优化问题来解决。方程组(1)的最小二乘解(或L2范数)等价于下面多维无约束优化问题(2)的全局近似最优解。
令目标函数ObjF(X)=FT(X)F(X),则无约束多维优化问题为:
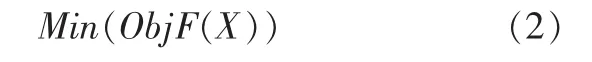
上述问题就转化为求解优化问题(2)。
3 问题的遗传算法设计
用遗传算法求解问题(2)时涉及的主要问题有参数编码方案、适应度函数设计、遗传操作算子设计、遗传算法基本参数选择、迭代终止条件等等。
3.1 参数编码方案
对问题(2),我们采用二进制多参数级联编码,即把参数向量X的每个分量先进行二进制编码得到各个子串,再把各个子串按参数的顺序排列在一起形成一个解个体。
3.2 适应度函数的设计
适应度函数是选择操作的最根本依据,它直接影响到遗传算法的性能。但适应度函数的设计没有一成不变的公式,只能根据具体问题进行设计,并通过仿真进行改进。对于优化问题(2),本文采用下式计算个体染色体的适应值:
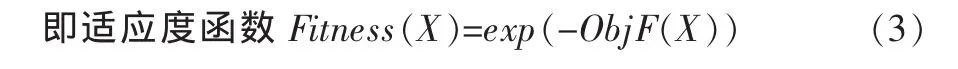
可见,目标函数值越大,其适应值越小,与优化问题
(2)一致,且该适应度函数变化趋势平缓,有利于趋近全局最优解。
3.3 遗传算法基本参数选择
群体规模l,交叉概率Pc,变异概率Pm的确定没有明确的数值,只有大概的范围。本文根据文献[5]的研究成果并结合所研究问题的实际取群体规模L为40~100,Pc为0.4~0.8,Pm为 0.001~0.01 。
3.4 遗传操作算子设计
选择算子采用排序选择,其主要着眼点是个体适应度之间的大小关系。即按适应度把个体从大到小排列,然后把序号在前的e个个体复制两份,覆盖序号在后面e个个体,而序号在中间的个体复制一份。这样整个群体大小并没有变化,它能保持一致的选择压力,能较好的抑制非成熟收敛。其中e的大小视群体规模而定,一般取1~5,当e=1时为杰出种子保留策略,本文采用这种策略。
交叉算子采用单点交叉,它能有效的保存较好的模式;变异算子采用基本位变异,即对个体染色体以变异概率Pm随机指定的某一位或某几位基因座上的基因值做变异运算。
3.5 迭代终止条件
虽然从理论上讲,遗传算法可以得到全局最优解,但实际上我们无法判断其确切的收敛时机,大多数情况下得出的是其近似最优解,这对于实际应用已经足够了。本文采用目标函数值ObjF(X)<1e-6作为迭代收敛条件。
3.6 遗传算法的具体实现步骤
(1)设定遗传算法的基本参数,初始化种群。
(2)根据式(3)计算每个个体的适应度。
(3)让群体中的个体进行上述的遗传操作,以产生新一代种群。
(4)判断是否达到3.5中所述的收敛条件。
(5)若是,则结束运算;若否,则重复(2)、(3)、(4)步直到算法收敛。
(6)对适应度最高的进行解码,从而得出方程(1)的最优L2范数解。
4 应用实例
本例取自文献[8]的[例7-5]。秩亏自由网平差的法方程为:
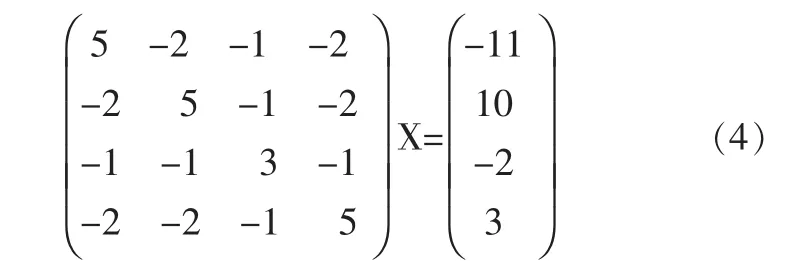
很显然,方程(4)的法方程系数阵的行列式│N│=0。为了验证本文算法的有效性,我们用上述遗传算法思想编程实现了求解该方程组。遗传算法参数设置为:群体大小L=80,交叉概率Pc=0.70,变异概率Pm=0.009.
附表给出了进化代数与目标函数值、方程解之间的情况。当迭代到280次,算法终止,得出X=(-1.499 96,1.499 96,-0.500 04,0.500 00),这与文献[8]用两种方法计算的结果几乎完全相同,但在实现方法上却简单了很多,省去了大量复杂的矩阵运算及需掌握的烦琐专业知识。
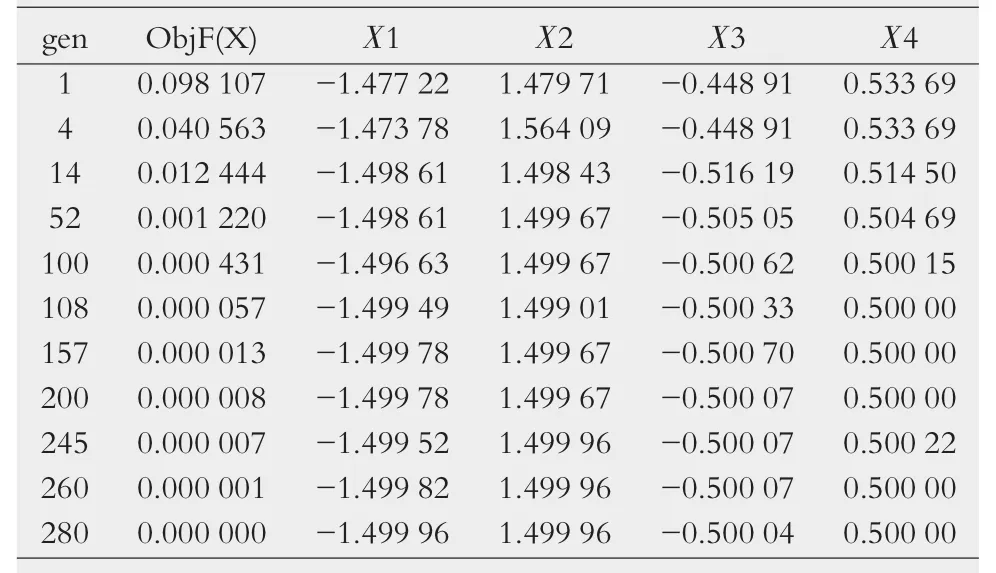
附表 进化过程中目标函数值及解的演变过程
5 结论
本文应用遗传算法直接求解秩亏方程组,实例结果表明,该方法能省去大量复杂的矩阵计算,且求解精度很高,完全满足工程的实际需要。本文所设计的算法比较合理,能有效地解决测量中秩亏自由网平差问题,具有较高的应用价值。但在算法设计中,遗传参数的选择还停留在定性阶段,需凭经验或通过大量的仿真来确定。一般情况下,我们希望能解决一类问题,而遗传算法依具体的问题不同,其参数的选择也不同,因此如何使参数能随着种群的进化过程进行自适应调整,从而得出问题的满意遗传解,是笔者下一步要研究的课题。
1 武汉测绘科技大学测量平差教研室.测量平差基础(第三版)[M].北京:测绘出版社,1996.
2 张文修,梁怡.遗传算法的数学基础[M].西安:西安交通大学出版社,2000.
3 周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.
4 王小平,曹立明.遗传算法—理论、应用与软件实现[M].西安:西安交通大学出版社,2002.
5 李敏强,寇纪凇,林丹,等.遗传算法的基本理论与应用[M].北京:科学出版社,2002.
6 李世玲,张富堂,李治.基于遗传算法的一类不确定性扰动下的系统参数辨识[J].系统仿真学报,2002,(5).
7 郝博,胡玉兰,卢有文,聂义勇.用遗传算法解病态线性方程组的研究[J].计算机工程与设计,1998,(3).
8 於宗俦,鲁林成.测量平差基础(增订本)[M].北京,测绘出版社,1983.
9 冯旭东,陈方.遗传算法的程序设计与实现[J].微机发展,1997,(6).

