空间结构动力灾变主动控制优化设计研究

王社良，董 元，代建波，赵 祥

(西安建筑科技大学 土木工程学院，陕西 西安710055)

随着建筑物跨度增大、高度增加以及结构形式日益复杂，按传统设计方法设计的工程结构在强地震、强风等作用下，很难完全避免损伤和破坏。因此，通过控制技术消除或减弱不利因素产生的影响得到了越来越多设计者的重视。被动、半主动控制技术在土木工程中已经得到了很好的研究及应用，而运用智能材料进行主动控制具有灵活性、智能性、高效性和适应性等优点，能够实现更好的控制效果，但目前在航空航天行业研究及应用较多，而在土木工程中的研究则刚刚起步。为了实现主动控制，设计适应于土木工程结构的主动元件，同时由于结构杆件较多，如何合理的布置主动元件以取得较高的控制效率，以及主动元件性能参数对结构不利因素的控制效果和影响是当前的热点研究问题[1，2]。

超磁致伸缩材料(Giant Magnetostrictive Material，简称为GMM)是一种新型的智能材料，具有输出力大、响应速度快、可靠性高、驱动电压低等特点。GMM在磁场作用下，长度及体积均发生变化而对外做功，去掉外磁场后，又可以恢复原来的尺寸，因而能高效地实现电磁能与机械能之间的相互转换，是重要的能量与信息转换功能材料[2]。用GMM制作的作动杆具有磁致伸缩应变量值大、能量转换效率高、能量密度大、工作电压低、响应速度快、承载能力强等无可比拟的优良特性，因而非常适宜用于结构振动的主动控制[3]。

1 超磁致伸缩作动器结构设计及性能

1.1 GMM作动杆设计原理

GMM元件在磁场的作用下发生形变从而产生作动力与位移，磁场由励磁绕组来提供，磁场大小可通过调节励磁绕组的电流进行控制。外加磁场的方向应与GMM元件产生变形的方向一致，当GMM元件中的磁场达到一定值时，元件发生变形。磁场去掉以后，GMM 元件基本自动恢复变形[4，5]。

1.2 GMM作动杆总体结构设计

图1为本文设计的GMM作动杆的总体结构示意图，图2为制造好的GMM作动杆实物图。此GMM作动杆包括外套、探测线圈、偏置线圈、激励线圈、线圈骨架、GMM元件、作动杆、连接杆、预压碟簧和调节螺母等，通电后偏置线圈、激励线圈提供叠加磁场，单层探测线圈用于测量磁场的大小。GMM是低磁导率材料，为了尽大可能的提高其工作效率，设计了由GMM元件和高导磁外套筒构成的闭合磁路，因为外套筒的高导磁率，磁通几乎全部被限制于外套筒中，磁力线沿着外套筒的路径流通，均匀穿过GMM元件且于其伸长方向一致，从而降低了漏磁。在GMM元件伸长方向上用碟簧加一足够大的反力，可起到预紧及增加位移输出量的作用。为了可以控制施加的力的大小，在弹簧上部设计了调解螺母以调节弹簧预压力的大小。当激励线圈通以电流信号时产生磁场，GMM元件产生伸长变化且伸长效应通过作动杆输出给作动对象，断掉电流信号后磁场消失，GMM元件恢复原来形状，完成此作动杆的作动效应。

图1 GMM作动杆总体结构示意图

图2 GMM作动杆实物图

1.3 GMM作动杆输出性能

通过电脑式伺服控制多功能力学试验机对制作的GMM作动杆进行了输出性能测试，该试验机自带精确的力学传感器及数据采集系统，控制精确、反应灵敏，能够满足本实验的要求(见图3)。在试验前对GMM元件施加了6 MPa的预压应力，对GMM作动杆进行测试得到其性能曲线如图4和图5所示。由GMM作动杆输入电流与输出位移关系图中可以看出，GMM作动杆在3A的电流强度驱动下可以产生72 μ m的位移量，并且重复性实验下稳定性较好；由GMM作动杆输入电流与输出力关系图中可以看出GMM作动杆在最大电流3A驱动下可以产生1 850 N的输出力，且输出力-驱动电流增益基本呈线性关系。

另外在试验中对GMM作动杆有无套筒的情况下电流与输出力的关系进行了对比，如图6所示，对比结果见表1。可以看出在同样大小的预压力和电流下有套筒时的输出力比没有套筒时要大很多，从而证明了高导磁外套筒很好的将磁通限制在套筒中，降低了漏磁现象。

图3 GMM作动杆输出性能测试试验

图4 GMM作动杆位移输出性能

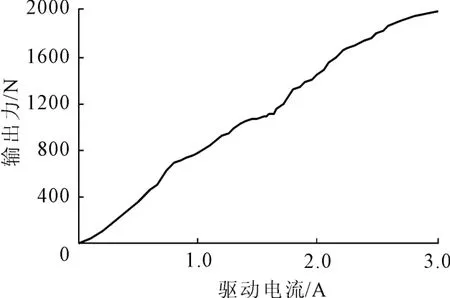
图5 GMM作动杆力输出性能

图6 无套筒时GMM作动杆输出性能测试

表1 GMM作动杆有无套筒的情况下电流与输出力的关系(预压力5MPa)

2 基于遗传算法的作动器位置优化

结构振动控制中的一个非常重要的问题就是确定作动器的布置位置，作动器位置布置合理，使用较少的作动器就可以达到较好的控制效果；反之，则会产生控制系统的硬件成本增加，复杂性增加，可靠性降低，控制效率降低等一系列问题。因此，对作动器的位置优化是非常必要的。

遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，它借鉴了达尔文进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，他能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最优解[6]。

2.1 位置优化的优化准则

受控结构的动力学方程可表示为[7]:

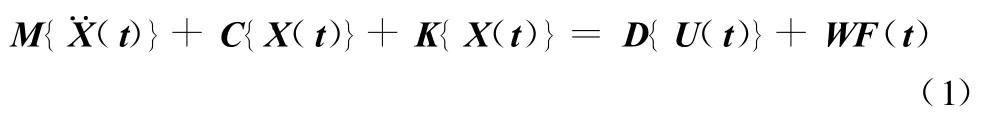
式中:M、C和K分别是质量、阻尼和刚度矩阵；{¨X(t)}、{﹒X(t)}、{X(t)}分别为加速度、速度和位移向量；F(t)为外扰力向量；{U(t)}为控制力向量；D为作动器的位置矩阵，它是由作动器的方向余弦组成；W为外扰力的位置矩阵。

不考虑外扰力的作用，将式(1)转换成模态方程。结构的第i个模态方程为:

对向量Bi进行奇异值分解得:

若模态qi为可控的，则矩阵Bi的奇异值矩阵可表示为:

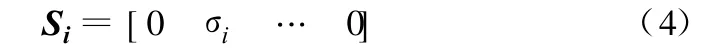
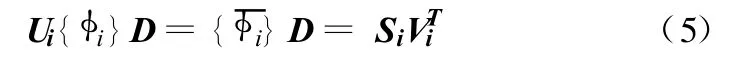
引入一组新的模态坐标{p}=[p1p2… pn]，则有:

利用新的模态坐标进行转换得:

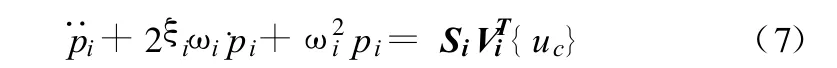
式中:γi代表了第i个受控模态的重要程度，因为结构振动的能量主要来自于地震，可以取γi为在地震位移反应谱上ωi所对应的值。J的值越大，作动器的布置就越优越。

2.2 优化模型

利用MATLAB软件建立优化模型，将上面求得的性能指标进行调整得到适应度函数:

式中:J0为调整前的适应度值；p为当前布置的作动器数目；m为预期布置的作动器数目。优化布置准则具有多样性，对于建筑结构，基于安全性的要求，运用最大耗能原则，J越大，代表结构的控制作用越好，作动器布置越优越。数学模型即:

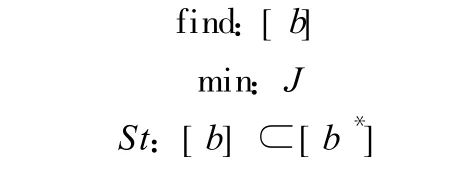
2.3 优化步骤

针对文中问题，采用以下步骤如图7所示。

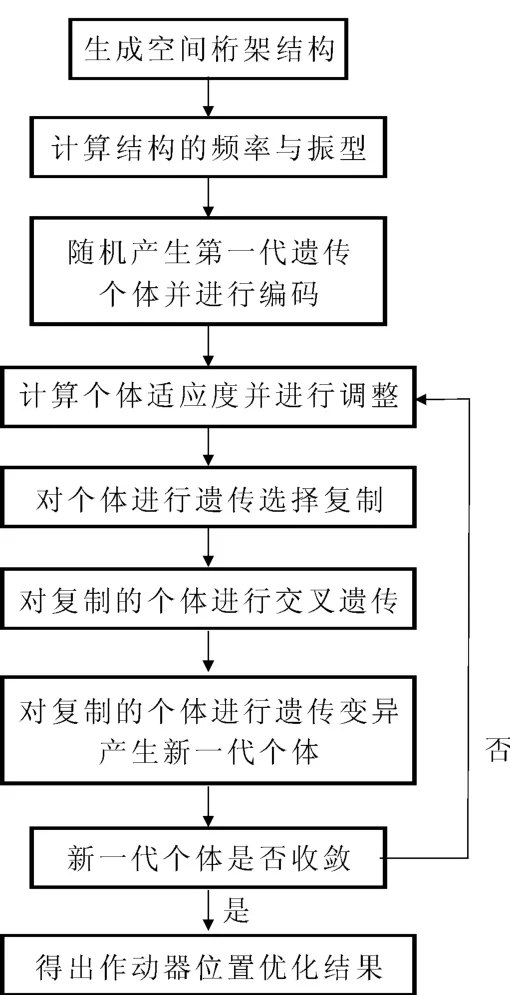
图7 遗传算法优化过程

(1)编码:采用二进制编码对个体进行编码，编码长度为 r(即结构一共有r根杆件)，若第i个基因值为1，表示该位置上布置了作动器，若第 i个基因值为0，表示该位置上没有布置作动器。

(2)初始种群:初始种群的生成原则是要求所生成的个体不同，尽可能保持初始群体的多样性，并符合约束条件，在进行群体更新时，用子代中适应度高于父代中的个体来替换父代中适应度较低的个体。一般初始种群数设置为10～100。

(3)适应度函数:适应度函数表明个体和解的优劣性。对于不同的问题，适应度函数的定义方式不同。

(4)交叉操作:设交叉概率为p，初始种群大小为nop，则随机选择出n=round(nop×p/2)对染色体作为双亲，对于本文实例，采用多点交叉法产生新的后代，每个子串对应一个优化位置信息。交叉概率一般取为0.4～0.99。

(5)变异操作:变异操作是对交叉生成的个体进行强制变化，防止过早的收敛而陷入局部最优解。对群体中，变异概率一般取为0.0001～0.1。

(6)选择:判断个体优良与否的准则就是各自的适应度值。根据各个个体的适应度值，按照一定的规则或方法从上一代的群体中选择出一些优良个体遗传到下一代群体中。

3 算例分析

3.1 计算模型

如图8所示的24杆空间杆系结构，所有杆件均采用钢管，弹性模量为210 GPa，密度为 7 850 kg/m3，杆件横截面积为0.001 m3，模型平面尺寸1m×1 m，竖向分两层，每层高1m。

图8 实验模型

3.2 作动器优化

本算例选取5个作动器的情况，结合遗传算法，进行优化设计。配置5个作动器时遗传算法的参数选择如表2所示。

表2 遗传算法优化参数设置

图9给出了配置5个作动器时适应度收敛曲线，表3给出了作动器优化结果。从图中可以看出，配置5个作动器时，种群的最佳适应度在第22代收敛，目标函数计算不足500次，而采用穷举法需要计算 C548=42054，可以看出，应用遗传算法可以高效、便捷的解决作动器优化布置这一类问题，并且结果收敛，有效。

表3 作动器位置优化结果

根据遗传算法优化结果，作动器布置位置如图10所示，可以看出，作动器的位置集中在空间桁架各阶模态的节点附近，也就是结构各阶振型变形最大的地方，具有明确的物理意义。同时，作动器的布置在均匀分布的同时比较集中于半边，是由于结构形式完全对称，优化布置位置同时具有对称性，并且随着作动器数目的增多更加趋于均匀。

图9 配置5个作动器时适应度收敛曲线

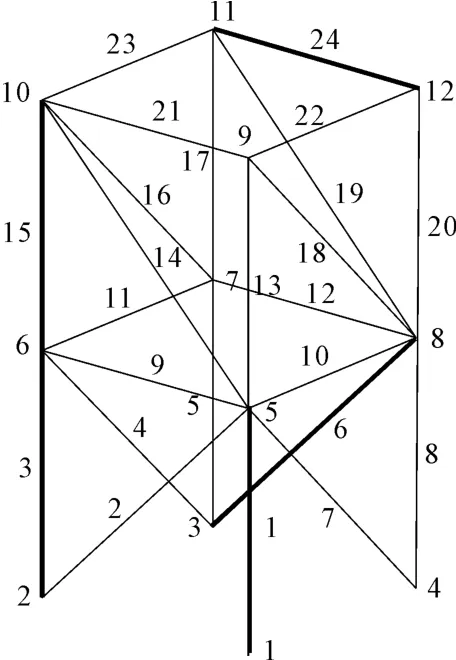
图10 5个作动器的布置位置

4 结 论

本文对GMM材料进行了深入研究，根据其特性制作了GMM作动杆并进行了输出性能测试，最后通过算例分析了将其集成到结构中后的布置位置优化问题，得到结论如下:

(1)GMM具有磁致伸缩应变量值大、能量转换效率高、能量密度大、工作电压低、响应速度快、承载能力强等无可比拟的优良特性，因而非常适宜用于空间结构动力灾变的主动控制。

(2)在充分掌握GMM的变形机理及磁控特性的基础上设计了一种GMM作动杆并对其进行了输出性能测试分析。分析了输入电流，高导磁套筒等因素对作动器性能的影响，从中总结出一系列的规律，为以后的研究提供了依据。

(3)试验结果表明GMM作动杆在较低的电流下可以输出较大的力，磁机转化效率很高，且输出力-驱动电流增益基本呈线性关系，具有良好的驱动性能，可以应用于空间结构的动力灾变控制中。

(4)遗传算法是随机搜索算法，不需要目标函数梯度，搜索结果不易陷入局部最优，适合于空间结构中作动杆布置优化这一离散优化问题的解决，运用这一方法，成功的进行了空间结构布置5个GMM作动杆的优化设计，结果表明与枚举法相比其效率提高显著。

[1]Cho S W，Kim B W，Jung H J.Implementation of modal control for seismically excited structures using magnetorheological dampers[J].Journal of Engineering Mechanics，2005，131(2):177-184.

[2]党 育，霍凯成，瞿伟廉.智能隔震结构的模态控制[J].华中科技大学学报(城市科学版)，2008，25(4):130-132.

[3]李 梅，吕银芳.超磁致伸缩材料及其应用[J].现代电子技术，2005，18(2):114-117.

[4]方紫剑，王传礼.超磁致伸缩材料的应用现状[J].煤矿机械，2006，27(5):725-726.

[5]朱厚卿.稀土超磁致伸缩材料的应用[J].应用声学，1998，17(5):3-10.

[6]雷英杰.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社，2005:2-5.

[7]欧进萍.结构振动控制—主动、半主动和智能控制[M].北京:科学出版社，2003:39-44.

[8]张东昱.双层柱面网壳主动控制及其优化研究[D].北京:北京工业大学.2001.