改进的传递系数法

童广勤，苏爱军

（1.中国地质大学（武汉）a.研究生院；b.三峡中心，武汉 430074；2.水利部长江勘测技术研究所，武汉 430011）

改进的传递系数法

童广勤1a，2，苏爱军1b

（1.中国地质大学（武汉）a.研究生院；b.三峡中心，武汉 430074；2.水利部长江勘测技术研究所，武汉 430011）

根据刚体极限平衡理论，以准超载法为基础，推导了改进的传递系数法的递推公式及累计求和表达式。论证了传递系数法仅仅是滑坡所有条块间作用力均不小0时，改进传递系数法特解的近似解；在此条件下，可用传递系数法替代改进的传递系数法求解滑坡稳定系数。给定安全系数后，在滑坡推力较大时（如1 000 kN／m），用传递系数法替代改进的传递系数法基本可行；其他条件下，尤其是当滑坡所有条块间出现拉应力时，用传递系数法计算滑坡稳定系数和滑坡推力均存在安全隐患。

滑坡；稳定性评价；传递系数法

1 概 述

采用条分法进行滑坡稳定性评价时，引入假定条件的合理性一直受到人们普遍关注。Morgenstern＆Price最早提出解的合理性限制，认为所获得的解必须满足以下条件：①条块间不产生拉力；②作用于土条界面上的剪力不超过以摩尔-库仑法则提供的抗剪强度。

同时，Morgenstern＆Price还提出了这样的推论：不同的关于土条作用力的假定，只要满足上述2个合理性条件限制，相应的稳定系数彼此相差不大。

作为条分法之一，目前应用最为广泛的传递系数法是《建筑地基基础设计规范》（PGB50007－2002）和《岩土工程勘察规范》（GB50021－2001）规定采用的滑坡稳定性评价及计算滑坡推力方法，适用于不同形状滑动面的滑坡。由于各种原因，采用传递系数法进行滑坡稳定性评价时，常常会出现不满足Morgenstern＆Price合理性限制的情况，归纳起来存在以下3个方面的问题：

（1）不满足Morgenstern＆Price提出的合理性限制条件①时，滑体条块间出现拉应力，计算所得到的滑体整体稳定系数偏大［1］。原因主要有2个方面：其一，滑坡体实际上由2大部分或几大部分组成，地质结果认定的滑动面起伏较大，并不是连续的最危险滑动面；其二，由于外部荷载施加的部位和方式不一，本应为整体性的滑坡演变为前缘局部牵引式滑坡，滑坡在某种状态下达到分段平衡。其结果表现为靠近剪出口段稳定系数小，远离剪出口段稳定系数大，结合部位的一些条块间必然出现拉应力。实际上，采用累计求和公式表达的现行条分法的各种具体方法基本上不能自动满足Morgenstern＆Price提出的合理性限制条件①，不适合进行牵引式滑坡的稳定性计算。

（2）由于传递系数法假定条块间作用力合力（剩余下滑力）的倾角与上一条块的滑动面倾角一致，当上一条块的滑动面倾角较大时，不可避免会出现一些条块作用于其界面上的剪力超过摩尔-库仑法则的现象，即Morgenstern＆Price提出的合理性限制条件②得不到满足。其结果是计算所得到的滑体整体稳定系数偏大［1，2］。

（3）当滑动面出现反倾时，可能出现后一滑块超覆于前一滑块滑动的不合理现象。尽管传递系数法在理论和实践上存在上述不足，但一般情况下，仅滑坡后缘存在少数条块不满足Morgenstern＆Price提出的合理性限制条件②的情况，对所计算滑体整体稳定系数影响不大［2］。根据Morgenstern＆Price的推论，这一情况对所计算滑体整体稳定系数影响也不大。现行规范通过适当扩大安全系数，基本上规避了其对滑坡防治工程安全的影响。

应用传递系数法进行人工边坡、土坝堤防的稳定性评价，不会遇到第一个问题，但是进行自然斜坡或滑坡稳定性评价时，出现第一个问题的可能性较大。而该问题往往被人们所忽视，导致极大的潜在风险。本文主要从理论上探讨对传递系数法改进和完善，在遵从现有规范的前提下，克服传递系数法存在的第一个方面的问题。

2 改进的传递系数法的基本公式

2.1 递推公式

与传递系数法一样，假定条块间作用力合力（剩余下滑力）的倾角与上一条块的滑动面倾角一致［1］（图1）。

图1 受力结构图Fig.1 Stressing state of a sliced b lock

设作用于条块的各种作用力以平行于该条块滑动面的剪应力τ和垂直于滑动面的正应力δ集中作用于滑动面上，滑动面强度受控于滑动面的内聚力和摩擦力。在滑动面破坏服从Mohr-Coulomb破坏准则的条件下，根据准超载法［2］的基本静力极限平衡公式（1）［2］，

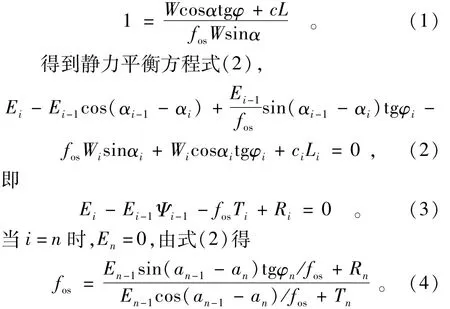
为保证Morgenstern＆Price提出的合理性限制条件①得到满足，引入限制条件：当Ei＜0，令Ei＝0。

联立式（3）、式（4）和Morgenstern＆Price提出的合理性限制条件①，得到由准超载法推导的改进的传递系数法递推公式一般表达式：

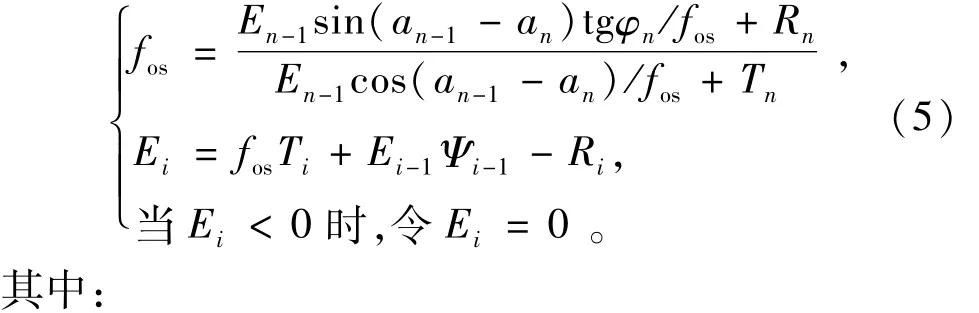
式中：fos为稳定系数；Ψi为第i条块的剩余下滑力传递至第i＋1条块时的传递系数；Ei为i条块剩余下滑力的合力（kN）；Wi为第i条块滑体重力（kN）；αi为第i条块滑动面倾角（°）；φi为第i条块滑带土的内摩擦角（°）；ci为第i条块滑带土的内聚力（kPa）；Li为第i条块滑动面长度（m）。各符号意义详见图1。

方程组（5）为改进的传递系数法递推公式的一般表达，作者已证明，对同一滑坡、相同边界条件，由方程组（5）计算所得到的稳定系数与基于强度储备法的不平衡推力法计算所得到的稳定系数完全一致［1，2］。

2.2 累计求和表达式

递推公式，方程组（5）还可以用累计求和公式方程组（6）表达。

对式（6）进行证明。根据静力平衡方程式（3）及引入限制条件：当Ei＜0，令Ei＝0，由Ea＝0，得：

（1）当n＝a＋1时，

故方程组（6）成立。

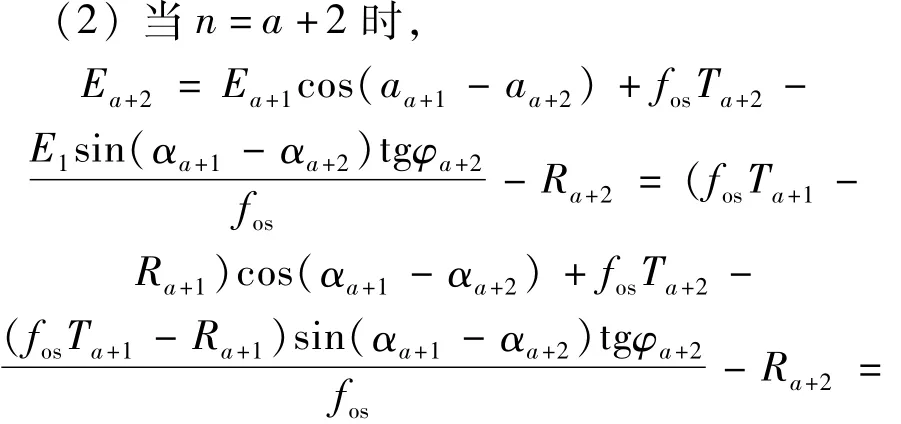
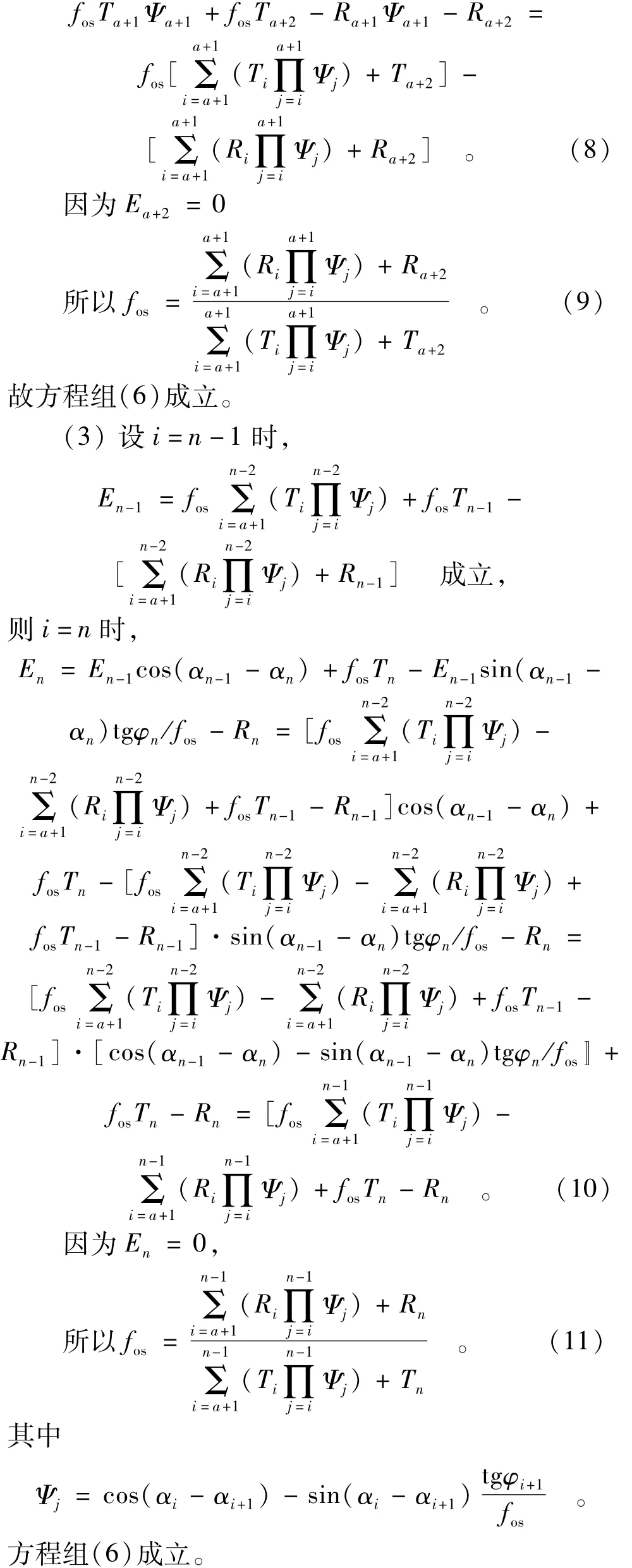
2.3 滑坡推力

当进行滑坡治理时，设安全系数为k，则各条块的滑坡推力计算表达式为

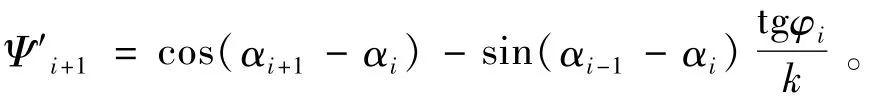
其中式中：Pi为滑坡推力（kPa），其倾角等于第i条块滑动面的倾角；Ψi－1为第i－1条块的滑坡推力传递至第i条块时的传递系数；αi为第i条块滑动面倾角（°）。

3 改进的传递系数法主要特点

3.1 改进的传递系数法与传递系数法的差异

将α＝0代入改进的传递系数法的累计求和表达式，则方程组（6）变为

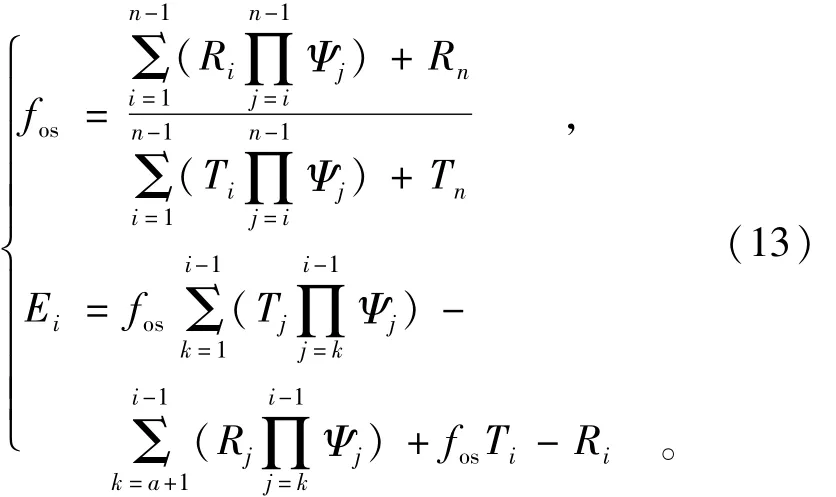
方程组（13）是滑坡所有条块间作用力均大于或等于零时，改进的传递系数法累计求和表达式方程组（6）的特解，与传递系数法表达式形式完全一致［3］。所不同的是方程组（13）为隐函数，其传递系数Ψi－1，必须通过试算才能求得滑坡稳定系数；而传递系数法的表达式为显函数，其传递系数Ψi－1＝cos（αi－1－αi）－sin（αi－1－αi）tgφi，可以较方便地求得滑坡稳定系数。很显然，传递系数法表达式仅仅是滑坡所有条块间作用力均大于或等于零时，改进的传递系数法特解方程组（13）的近似解。

从物理意义上说，传递系数法是视滑坡后缘至剪出n－1条块处于极限平衡状态，将各条块剩余推力投影到第n条块滑动面上，将第n条块滑动面上的抗滑力除以滑动力，由此求得滑坡稳定系数。而改进的传递系数法各条块的稳定系数和滑坡总体稳定系数相等。二者实际应用时的具体差异主要体现在如下3方面：

（1）给定剪切强度参数φ，C，当稳定系数小于1时，传递系数法计算所得到的稳定系数小于改进的传递系数法特解计算所得到的稳定系数；当稳定系数大于1时，传递系数法计算所得到的稳定系数大于改进的传递系数法特解计算所得到的稳定系数。稳定系数与1差别越大，改进的传递系数法特解与传递系数法计算所得到的稳定系数差别也越大。一般情况下，当稳定系数小于1.5时，二者相对差不超过2%。

（2）给定稳定系数进行反演分析、求解滑动面剪切强度参数时，给定稳定系数等于1，二者求得的剪切强度参数完全一致；对于正在蠕变的滑坡，给定稳定系数小于1，传递系数法求得的剪切强度参数比改进的传递系数法特解求得的剪切强度参数大；对于处于稳定的滑坡，给定稳定系数大于1，传递系数法求得的剪切强度参数比改进的传递系数法特解求得的剪切强度参数小。

（3）给定安全系数，传递系数法计算的滑坡推力小于改进的传递系数法特解计算的滑坡推力。给定的安全系数越大，传递系数法计算的滑坡推力越小。一般情况下，当安全系数小于1.25时（安全等级为Ⅰ级的滑坡基本工况所对应的安全系数），二者相对差不超过15%。滑坡推力越大，二者相对差越小。当滑坡推力大于1 000 kN时，传递系数法计算所得到的滑坡推力一般大于改进的传递系数法特解90%，当滑坡推力很小时（如单宽滑坡推力小于250 kN／m），二者相对差将超过15%。

3.2 改进的传递系数法用于牵引式滑坡稳定性评价

滑体条块间出现拉应力，表明滑坡分段平衡状态，靠近剪出口段稳定系数小，远离剪出口段稳定系数大，出现拉应力部位为二者的结合部位，滑坡的变形破坏方式为前缘局部牵引。

传递系数法不能通过计算机自动识别牵引式滑坡，并计算其稳定系数，所计算的是滑坡沿给定滑动面整体滑动时的稳定系数，计算所得到的稳定系数偏大［1］，可能遗漏不稳定的滑坡，从而导致灾难性后果。

改进的传递系数法通过导入当Ei＜0，令Ei＝0的必要条件，可利用计算机自动识别牵引式滑坡，并计算其稳定系数，克服了传递系数法的重大缺陷。

4 计算实例

4.1 滑体条块间不出现拉应力的情况

分别以湖北省三峡库区秭归县千将坪基岩顺层滑坡、石佛寺、重庆市万州区磨子坪、云阳寨坝第四系松散堆积体沿与基岩接触面滑坡和广西南宁市荣和山水美地半成岩岩质滑坡为例加以说明（表1）［2］，限于篇幅，只列出计算结果。

表1中，传递系数法与改进的传递系数法相比较，5个滑坡的稳定系数有3个相差不超过4‰；2个相差为1%，该2个滑坡由传递系数法计算的稳定系数均超过了1.2。在给定安全系数1.25的条件下，4个滑坡的滑坡推力有3个相差小于10%（由传递系数法计算的滑坡推力大于1 000 kN／m），1个滑坡的滑坡推力相差34%（由传递系数法计算的滑坡推力仅90 kN／m）。

4.2 滑体条块间出现拉应力的情况

以重庆市丰都南竹园滑坡为例［1］，滑坡物质组成主要为黏土夹碎石及少量块石。滑动面的内聚力为15 kPa，内摩擦角为12.5°，天然重度21.4 kN／m3，饱和重度22.5 kN／m3，地表荷载仅为少量的房屋，计算时不予考虑，考虑地下水的影响。计算剖面如图2，传递系数法和改进的传递系数法稳定系数计算结果见表2。在安全系数为1.20时（安全等级为Ⅱ的滑坡基本工况所对应的安全系数），滑坡推力见图2、图3。

图2 计算剖面示意图Fig.2 Sketch of calculation section

表1 典型滑坡稳定系数及最后条块的滑坡推力Table 1 Results about stability coefficient and thrust on the final slice block in typical landslides

从计算结果看，由于条块出现了负的剩余下滑力，传递系数法计算的稳定系数比改进传递系数法的稳定系大0.071。安全系数取1.2时，传递系数法计算得到的各条块的滑坡推力均比改进传递系数法要小（图3），最后一条块的滑坡推力要小50%（表2）。

表2 稳定系数及滑坡推力（安全系数取1.20）Table 2 Results about stability coefficient and thrust of the landslide w ith safety coefficient 1.20

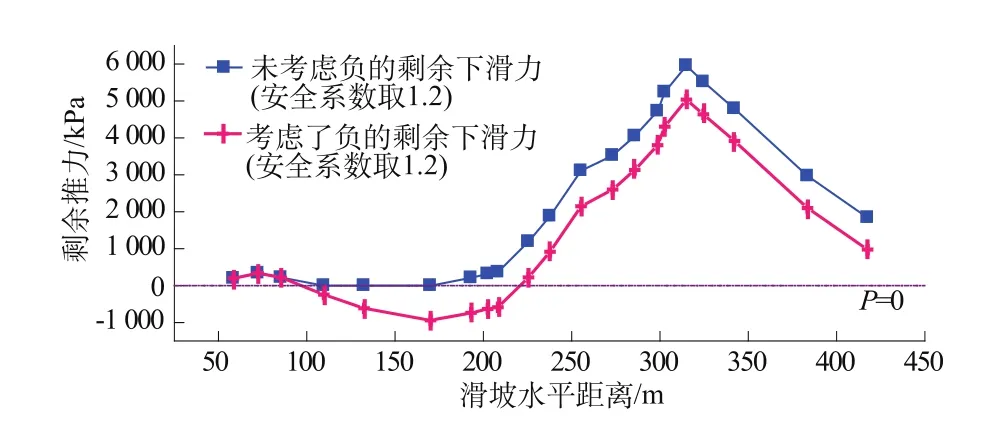
图3 改进传递系数法和传递系数法滑坡推力对比图（安全系数1.2）Fig.3 Contrast of thrusts obtained by improved transfer coefficientmethod and transfer coefficientmethod

5 结 论

综上所述，可以得到4点结论：

（1）改进的传递系数法是在滑动面破坏服从Mohr-Coulomb破坏准则的条件下，根据准超载法，基于静力极限平衡条件所推导的半精确条分法，无条件满足Morgenstern＆Price提出的合理性限制条件①。传递系数法仅仅是在滑坡所有条块间作用力均大于或等于零的条件下，改进的传递系数法特解的近似解。

（2）在滑坡所有条块间作用力均大于或等于零的条件下，用传递系数法代替改进的传递系数法所得到的稳定系数相差很小；当滑坡推力大于1 000 kN／m时，二者计算所得到的滑坡推力相差也不大（一般不超过10%），但当滑坡推力较小时，二者计算所得到的滑坡推力相对差较大。因此，在滑体条块间不出现拉应力的情况下，用传递系数法代替改进的传递系数法，计算滑坡稳定系数是可行的；当滑坡推力大于1 000 kN／m时，用传递系数法代替改进的传递系数法计算滑坡推力问题不大。但当滑坡推力较小时，二者计算所得到的滑坡推力相对差较大，应谨慎对待。

（3）当滑坡条块间出现拉应力时，传递系数法不满足Morgenstern＆Price提出的合理性限制条件①，计算所得到的滑体稳定系数明显偏大，可能遗漏不稳定的滑坡，在给定的安全系数条件下，所计算的滑坡推力严重偏小，可能导致灾难性的后果。

（4）虽然改进的传递系数法稳定系数计算公式为隐函数，相比显函数的传递系数法计算复杂，但现今计算机技术的高度发展，使得隐函数的计算不成为难题。为安全起见，在遵从现有规范的前提下，用改进的传递系数法取代传递系数法势在必行。

［1］ 苏爱军，冯明权.滑坡稳定性传递系数法的改进［J］.地质灾害与环境保护，2002，13（3）：51－55.（SU Aijun，FENG Ming-quan.The revisionon of transfer cofieientmethods for landslide stability［J］.Journal of Geological Hazards and Environment Preservati，2002，13（3）：51－55.（in Chinese））

［2］ 苏爱军.滑坡稳定性评价原理与方法——条分法的改进［M］.武汉：中国地质大学出版社，2008.（SU Aijun.The Principle and Method for Landslide Stability E-valuation-Revision on Sliced Method［M］.Wuhan：China University of Geosciences press，2008.（in Chinese））

［3］ GB50021－2001，岩土工程勘察规范［S］.（GB50021－2001，Code for investigation of geotechnical engineering［S］.（in Chinese））

（编辑：王 慰）

Improved Transfer Coefficient M ethod

TONG Guang-qin1，2，SU Ai-jun2
（1.hina University of Geo-science China，Wuhan 430074，China；2.Changjiang Research Institute of Geotechnique＆Survey.MWR.，Wuhan 430011，China）

In this paper，according to the limit equilibrium theory of rigid body，the recursion formula and the cumulative summation formula of improved transfer coefficientmethod were created，based on the pseudo-overloading method.Itwas demonstrated that the transfer coefficientmethod is the approximate solution of especial solution ofthe improved transfer coefficientmethod，while the force of inter-slice ismore than zero or equal to zero.In this case，it is feasible to calculate the stability coefficient using the improved transfer coefficientmethod instead of the transfer coefficientmethod.When the factor of safety is given，if the landslide thrust is quite greater（such as1 000 kN／m），it is basically feasible to use the improved transfer coefficientmethod instead of the transfer coefficient method.In other cases，there exists some risk of safety by using transfer coefficientmethod to calculate landslide stability coefficient and landslide thrust，particularly when tensile stresses arise among all landslide slices.On the premise in compliance with the existing norms，the improved transfer coefficientmethod replacing the transfer coefficientmethod is imperative.

landslide；stability assossment；transfer coefficientmethod

TU457

A

1001－5485（2010）06－0043－06

2009-06-17；

2009-12-25

童广勤（1977-），男，湖北仙桃人，高级工程师，博士研究生，主要从事地质灾害的成因及防治技术研究，（电话）027-82927007（电子信箱）tongguangqin＠163.com。