海流对潜布水雷水中弹道的影响研究*

顾 闯 逄洪照 张 永

(海军潜艇学院 青岛 266071)

1 引言

水雷兵器使用灵活,易布难扫,造价低廉,攻守兼备,素有“兵力倍增器”之称。潜艇的隐蔽性好,突击威力大,是我海军的杀手锏兵力之一。利用潜艇平台装载不同型号的水雷武器,可以对敌防守严密的港口、近岸航线和必经航道等实施攻势和机动布雷,以达到瘫痪其交通、牵制其兵力、迟滞其行动之目的。随着水雷战与反水雷战在局部战争中地位的不断加强,世界各国海军越来越重视潜艇布雷技术和布雷战法的研究。水雷经潜艇鱼雷发射管发射出管后,海流、海浪等海洋力学环境,对水雷的运动将产生直接影响,间接对水雷的作战效能产生影响[1～2]。

2 潜布水雷水下无动力运动的六自由度空间弹道数学模型的建立

本文研究的某型潜布水雷是一关于横轴、纵轴对称的轴对称体,雷头是椭球体形,雷体部分是圆柱体形,质心与浮心不重合。

2.1 潜布水雷水下运动参考坐标系的确定

参考坐标系,简称坐标系,是指为了确定物体的位置和描述其运动而选作标准的另一物体。在对物体位置进行测量和定位时,在参考物上必须选定一个原点作为距离的起点,参考面和参考线作为角度计量时角度所在平面和零的基准,因此坐标系包括原点、参考线和参考面三要素。本文所选用的坐标系有:雷体坐标系oxyz、地面坐标系ox0y0z0、速度坐标系ox1y1z1,其中雷体坐标系oxyz的定义如下所示,为雷体坐标系原点选在水雷浮心,坐标系ox轴与雷体的纵轴重合,指向水雷头部,oy轴位于水雷纵对称面内,与ox轴垂直,且指向上方,oz轴垂直于oxy平面,指向按右手法则确定。地面坐标系ox0y0z0、速度坐标系ox1y1z1的定义、运动学参数选择位置坐标 x0、y0、z0、速度 vx、vy、vz、姿态角 θ、ψ、φ、弹道角、角速度 、攻角 α、侧滑角 β等各参数物理意义及量纲同文献[3]。

为了清楚起见,本文中凡是雷体坐标系中量的表示均不带下标,地面坐标系中量的表示用下标0,速度坐标系中用下标1。例如,vx表示速度在雷体坐标系ox轴上的分量,vox表示速度在地面坐标系ox轴上的分量,v1x表示速度在速度坐标系ox1轴上的分量。

2.2 作用在水雷上的力及力矩分析

潜布水雷水下无动力运动时所受的流体动力和力矩:重力和、浮力和流体动力及其力矩。水雷的流体动力按运动形式可分位置力、阻尼力和附加惯性力。作定常直线运动时,水雷受到的位置力主要受运动速度、加速度、攻角、侧滑角大小的影响,在速度坐标系中的分量为位置阻力、位置升力和位置侧力,相应的力矩在雷体坐标系中的分量为位置俯仰力矩和位置偏航力矩。水雷作定常旋转运动受到的阻尼力,受直线运动速度和角速度的影响,在雷体坐标系中的分量为阻尼升力、侧力以及阻尼俯仰力矩和偏航力矩。流体惯性力及力矩是水雷作非定常运动时所受的流体动力,其大小与雷的运动速度变化快慢及其附加质量大小有关。水雷的水下弹道仿真数学模型建立在雷体坐标系中,所以计入数模中的雷体的力和力矩须投影变换到雷体坐标系中。

2.3 水下无动力运动弹道数模

根据刚体运动的坐标系及转换矩阵推导出水雷的运动学方程组,根据刚体运动的动量定理和动量矩定理得到其动力学方程组[3]。联立水雷的运动学方程组、动力学方程组,可以得到潜布水雷水下无动力运动弹道数学模型由以下一阶常微分方程组构成。

3 海流对弹道影响的分析

自然界的海流受多种因素的影响与制约,是非常复杂的,海流的大小和方向与测试点当地的地理位置有关,与测试点距水面的深度及海底的高度有关,还与测试的时间有关,是空间与时间的函数,并且还具有很大的随机性。本文在研究海流对水雷散布误差的影响时,不考虑建立海流数学模型的问题,假定海流的速度已知,且为常量,即:

式中:→vw0为海流在地面坐标系中的速度矢量;vwx0,vwy0,vwz0为海流速度→vw0在地面坐标系中的三个分量,根据上述假设,海流速度的三个分量为常数,m/s。

当水雷在海流中运动时,相当于在原流场上叠加了海流的流场 ,可用矢量表示为=+式中为水雷在地面坐标系中的速度矢量为水雷相对于海流的速度矢量。

研究水雷的运动特性,当考虑海流作用时,作用在水雷上的流体动力,如阻力、升力、阻力矩、升力矩等取决于水雷相对于流体的速度、攻角和侧滑角。因此,水雷动力学模型中各运动学参数在这个意义上都是相对流体的,只有在无海流时,获得的运动学参数才是相对于地面坐标系的,即在水下弹道数模中须采用潜布水雷自身的速度叠加上流体介质速度的相对速度[4],即→vtw0=→v0-→vw0表示成分量形式,转换到雷体坐标系中为:

式中:上标“0”为时间为零点时的参数值,即初值;下标“0”为地面坐标系中的参数值;为无海流时水雷速度在地面坐标系中的初值。

同理,考虑海流作用时的攻角、侧滑角、弹道角等的初值可表示为:

根据2.3节中的水雷空间运动模型解算出的水雷空间位移是相对于地面坐标系的,为了求解海流对水雷弹道的影响,需要通过绝对运动、相对运动及牵连运动的关系,获得水雷在海流中运动时相对于地面坐标系的运动参数。为此,当考虑海流作用时,需对水雷空间位移进行修正。修正公式为:

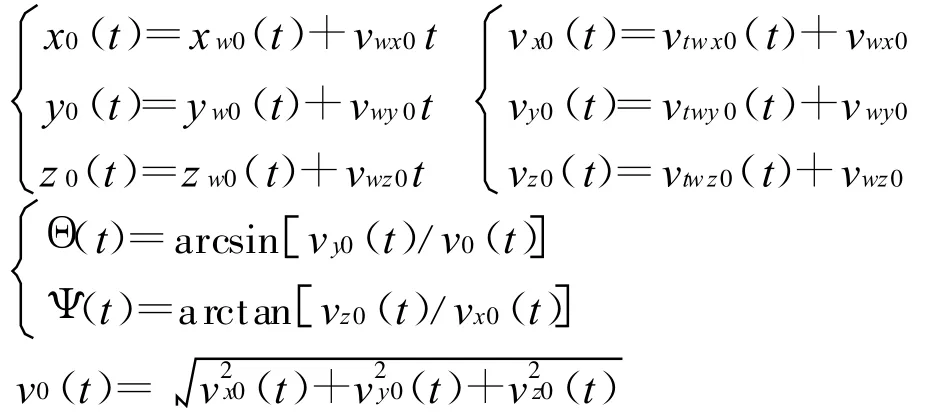
式中:x0(t),y0(t),z0(t)为水雷在有海流时,经过时间t后在地面坐标系中的位移分量;xw0(t),yw0(t),zw0(t)为由运动方程组解算出的在海流坐标系中的三个方向位移;vx0(t),vy0(t),vz0(t)为水雷在有海流的运动过程中,时刻t水雷速度在地面坐标系中的三个分量;vtwx0(t),vtwy0(t),vtwz0(t)为由运动方程组解算出的在海流坐标系中,时刻t水雷速度的三个分量;Θ(t),Ψ(t)为在地面坐标系中水雷弹道曲线t时刻的弹道倾角和弹道偏角。

4 弹道仿真实例

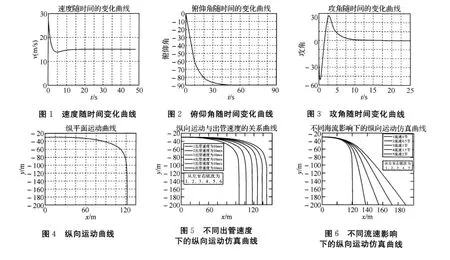
初始条件:设某水雷在水下30m发射,出管速度为 15m/s,初始条件为 x0=0、y0=-30、z0=0,速度vx=15、vy=vz=0,姿态角、弹道角、角速度、攻角、侧滑角全部为0;在上述条件下,速度随时间变化曲线、俯仰角随时间变化曲线、攻角随时间变化曲线、纵向运动曲线以及不同出管速度、不同海流作用下的弹道仿真曲线如图1～6所示。

从以上仿真曲线可知,水雷出管后初始阶段,由于受海水阻力,速度迅速减小,由于重力力矩等因素的影响,雷头将向下偏转,此时雷速vox分量将逐渐减小,voy分量逐渐增大,导致攻角α逐渐增加,俯仰角θ逐渐增大,位移 x0随雷速 vox增加。当雷体偏转到一定角度、水雷速度减小到一定值时,攻角开始减小,最后稳定在0°,俯仰角稳定在90°,雷速趋于稳定,各项参数也趋于稳定。由不同流速流向、不同水雷出管速度条件下水雷的弹道仿真曲线可知,出管速度越大,同向海流流速越大,水雷的水平位移越大。其中海流对水雷的水平位移影响较大,出管速度对水雷的水平位移影响较小,较海流对水雷的水平位移影响可以忽略不计。

5 结语

本文分析了某型潜布水雷在水下作无动力运动时的受力情况,并在建立其运动学、动力学模型和海流影响分析的数学模型的基础上,建立了其水六自由度空间弹道数模,并用Matlab软件实现了不同流速、不同水雷出管速度条件下弹道仿真,仿真结果结果显示水雷弹道稳定,符合实际情况,结果合理。本文的仿真结果可以为潜艇布雷作战方案和技术预案的制定以及选择布雷时机提供参考依据,特别是对于港口、航道的实施准确布雷,提高潜艇的布雷作战能力和水雷的作战效能,为我国潜射水雷弹道理论的深入研究、新型水雷水中弹道的设计和装备器材的研制,提供参考依据和借鉴具有重要的理论价值和军事应用价值。

[1]Gunther Bruckner.Command and control system for remote mine sweeping[J].Naval Force,2001(1):8～13

[2]Commander Steven A.Borden United States Navy,Mine Countermeasure:A Comparative Analysis of US Navy Mine Countermeasures 1999 VS 2020,ADA377403

[3]张宇文.鱼雷弹道与弹道设计[M].西安:西北工业大学出版社,1999:42～49,77～83

[4]严卫生.鱼雷航行力学[M].西安:西北工业大学出版社,2005:64～66

[5]陈杰.Matlab宝典[M].北京:电子工业出版社,2007

[6]文刚,玄兆林.不同流速流向下的某型空投水雷水下散布研究[J].武汉理工大学学报,2007,(31)1