基于实测数据的海杂波特性分析*

赵传辉 曲付勇 安江华

(海军航空工程学院1) 烟台 264001)(92854部队2) 湛江 524054)

1 引言

对于在海洋背景环境下使用的雷达来说,接收机将接受到大量的杂波,目标信号往往淹没于各种杂波和热噪声中。为了实现对目标的检测、跟踪与识别等处理,找到能够有效把目标信号和杂波区分开的特征量是关键;杂波特性的研究利用现有的各种数据分析方法深入分析杂波表象背后的本质规律和区别于目标的数值特征量,并因此而建立准确杂波模型,是设计最优检测算法和性能评估的客观要求,对于雷达的成功设计有重要的作用[1]。

在诸多雷达杂波背景中,海杂波以其随雷达极化方式、工作频率、天线视角及海情、风向和风速等多个因素的变化而呈现明显的非平稳、非高斯性。特别是所谓的“海尖峰”和目标类似,对正常检测影响十分严重。因而,为了设计针对海杂波的最佳信号处理算法,充分分析和认识海杂波的特性是首要工作。

在瑞利、对数正态、韦布尔等经典杂波幅度统计模型的基础上,Ward首先提出了采用K分布作为海杂波分布的统计模型[2]。由于较好地刻划了海杂波的形成机理,因此受到普遍关注。

值得重视的是,海杂波与海洋表面的形状是紧密相关的,而海洋表面在各种因素的作用下呈现出一种复杂、无规律的、永无止境的运动状态,并且在不同的海域表现出显著的地域特性;以目前对海杂波研究的程度来说,确立一种统一形式的杂波模型不现实,尤其是在海杂波中还混杂有地杂波、气象杂波、热噪声等成分时更难准确地描述杂波的幅度变化特征和时空相关特性,比较合理的方法是根据具体地理区域进行真实测量,以实验数据为基础建立起来的杂波模型更有说服力。

本文基于实际测量得到的数据进行杂波特性分析,主要讨论海杂波情况下杂波的幅度分布模型,采用韦布尔分布,对数正态分布和K分布进行拟合并进行模型检验,给出结果,最后得到有意义的结论。

2 海杂波的幅度模型

文献[3]认为当用高分辨力雷达(脉冲宽度小于 0.5μ s)在低视角(小于5°)观察海面时,海杂波幅度上呈现出非高斯性。意味着其概率密度分布将偏离高斯分布,杂波幅度常用韦布尔分布,对数正态分布和K分布模型来描述,对于测量数据分别采用这三种模型进行拟合。

2.1 杂波幅度分布分析

海杂波的幅度分布是建模中重要的一个内容,在众多提出的模型中最常用来描述海杂波幅度模型是韦布尔分布模型,对数正态模型和K分布模型[4],它们有更好的拟合准确度,在此对其概率密度函数、概率分布函数等进行简要说明。

2.1.1 韦布尔分布

概率密度函数为:

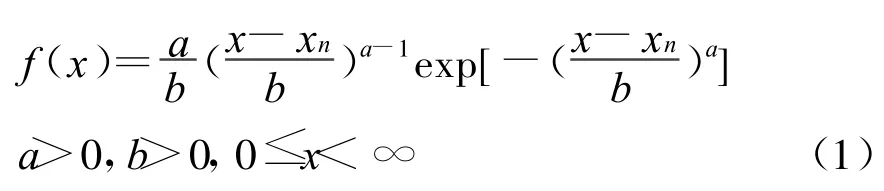
式中参量xn、a、b分别称为韦布尔分布的位置参量,形状参量和标度参量。

概率分布函数为:

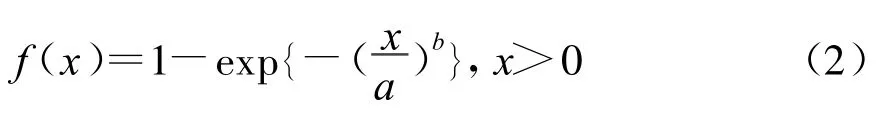
韦布尔分布的动态范围介于瑞利分布和对数正态分布之间,能在更宽广范围内精确表示实际的杂波分布。通常,在高分辨率雷达、低入射角的情况下,一般海情的海浪杂波能够用韦布尔分布精确地描述,地物杂波也能用韦布尔分布描述。且韦布尔分布的形状参数p随着擦地角的增大而增大,使韦布尔分布能模拟越尖锐的杂波。

2.1.2 对数正态分布

概率密度函数为:

概率分布函数为:

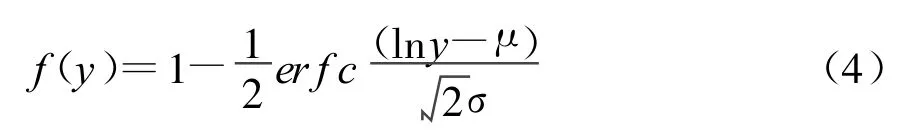
式中,erf c(◦)是余误差函数,μ称为尺度参数,σ称为形状参数。

对数正态分布适用于低擦地角(小于5°)时的高分辨率水平极化雷达所观测到的杂波数据,其标准差σ随入射角的减小而增大。

2.1.3 K分布

K分布概率密度函数:

其中,v＞-1是形状因子,α＞0是尺度因子,Kv-1(◦)为v-1阶第二类修正的Bessel函数。

累积概率分布函数:

对于大多数杂波,v=0.1-∞,当v→∞时,杂波分布接近于瑞利分布;对于高分辨率低地角的海杂波,v的取值范围是[0.1,3]。Γ[◦]为伽马(Gamma)函数,kv(◦)为第二类修正Bessel函数。K分布是一种复合分布模型,它把海杂波回波能量描述为两个因子的乘积,第一部分是斑点分量(即快变化分量),由大量散射体(主体波形结构上的小碎波)反射进行相参叠加构成,服从指数分布,有弱的相关性,可通过频率捷变处理去除;第二部分是基本幅度调制分量(即慢变化分量,又称均值分量),反映了与海面大面积结构有关的散射束在空间变化的平均电平,用Gamma分布描述,并且相关性较强。K分布适用于描述高分辨率雷达的非均匀杂波,多见于高海况等级的海杂波的描述。

3 海杂波的频谱特性

风速的影响使得雷达杂波单元内各散射体具有一定的速度散布,雷达平台的运动以及机扫天线的转动扫描也带来杂波速度的散布,从而使雷达杂波具有一定的功率谱。而在雷达信号处理的某些场合需知道雷达杂波功率谱分布。常见的雷达杂波的功率谱分布有:高斯型、立方型、指数型,它们相应的归一化功率谱密度函数有以下几种[5]。

3.1 高斯谱模型

高斯谱模型是一种最早提出的,也是各种文献中用得最多的杂波功率谱模型,它可以表示为:

式中,fd为多普勒频率,σf为杂波谱分布的标准差。

3.2 柯西谱模型

柯西谱模型也称马氏谱,它可以表示为:

式中,fd为多普勒频率,f3dB是 fd=0,3dB宽度对应的频率。

3.3 全极谱模型

全极谱能更好地描述杂波谱的“尾巴”,它的表达式为:

式中,fd和f3dB意义同式(8),n的典型值为2～5,当n=2时,全极谱即为柯西谱,当n=3时,即为通常所说的立方谱。

由随机过程知功率谱与自相关函数互为傅里叶变换,因此,我们通常通过自相关函数来研究功率谱。

4 海杂波数据

图1是I通道数据经过处理后得到的中频时域信号。

图1 输出的时域信号

4.1 I通道的数据分析

对 I通道的数据进行分析,一般采用斜度(skewness)和峰度(kurtosis)作为衡量一种分布是相对分散或集中的量,定义如下:

斜度衡量一个变量关于其均值的不对称度,正值时表明其均值右边有不对称的拖尾;负值时表明其均值左边有拖尾。峰度衡量一种分布的相对尖锐或平坦程度。对于高斯分布,这两个值都等于0,因此它们说明一种分布偏离高斯分布的程度。

对海杂波的数据进行斜度和峰度分析,其结果显示数据的斜度值大于零。所以其分布函数相对于其中心分布而言,有位于右边的不对称拖尾,这说明杂波幅度有较长的拖尾。峰度较大,说明通道数据比较集中,形成较大的概率波峰。

4.2 试验结果

下面分别用2.1节中的三种幅度分布模型来拟合实测的海杂波幅度分布曲线。

由图3可以看出k分布可以较好地描述海杂波的幅度分布。

由图5可得出,海杂波的频谱符合高斯谱模型,也符合我们一般用高斯谱模型来描述海杂波频谱的规律。

5 结语

本文分析了几种常用的海杂波幅度分布模型,并用其拟合实测的海杂波幅度分布,得出海杂波幅度可用k分布进行很好的描述。对于海杂波的频谱,由试验结果可以看出,高斯谱模型能较好地描述海杂波的频谱。

杂波的特性对于杂波的仿真有着重要的意义。本文从幅度分布和频谱特性两方面进行了论述,并给出了基于实测数据的试验结果,为模拟杂波环境提供了理论基础。

[1]欧阳文,何友,方伟.基于实测数据的海杂波特性分析[J].系统仿真学报,2006

[2]K.D.Ward.Compound Representation of High resolution[J].Sea Clutter.Electronics Letters,1981,17(16):561～563

[3]Chan H C.Radar sea-clutter at low grazing angles[J].IEE Proc.-F,1990,137(2):102～112

[4]温玉.雷达无源干扰建模及杂波抑制方法研究[D].成都:电子科技大学硕士学位论文,2005,5

[5]兑雅娟.雷达杂波相关特性与仿真[J].火控雷达技术,2006,36(1):51～55